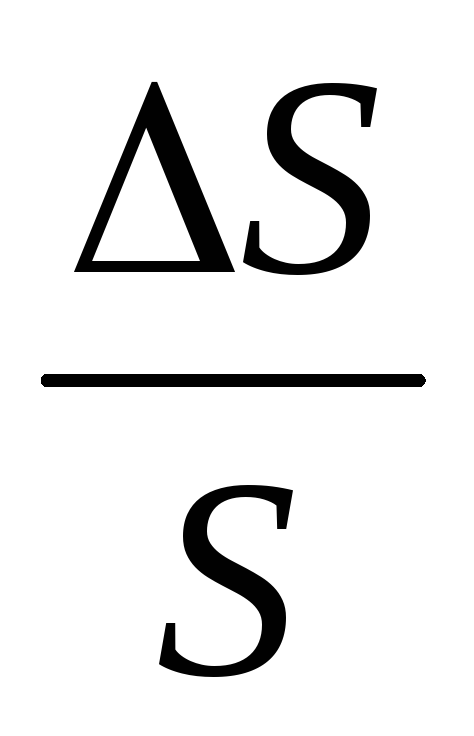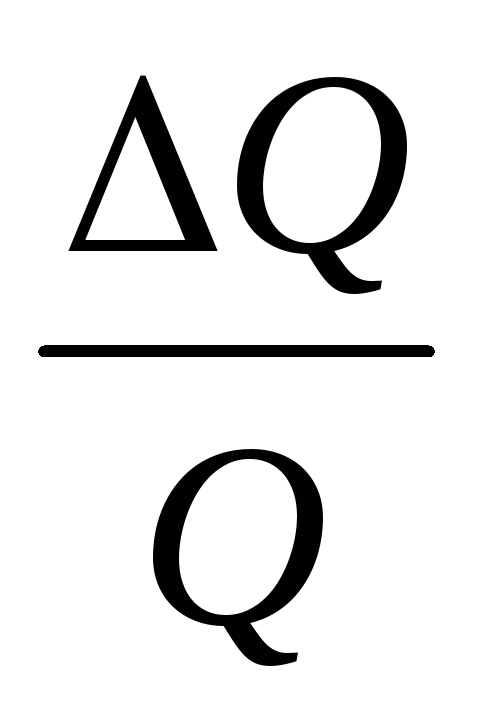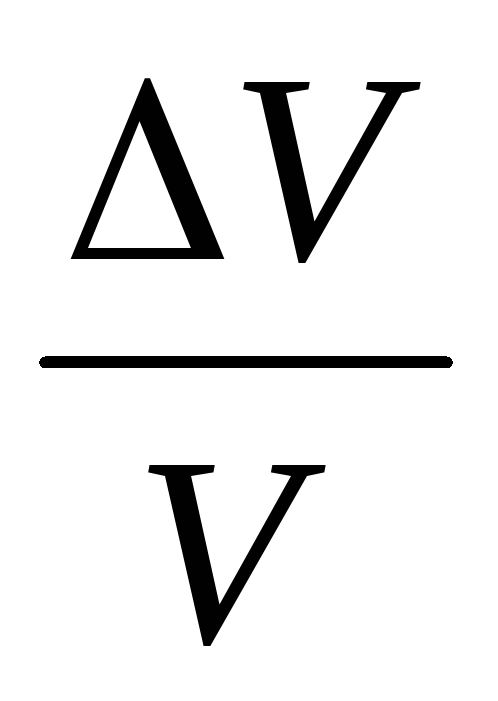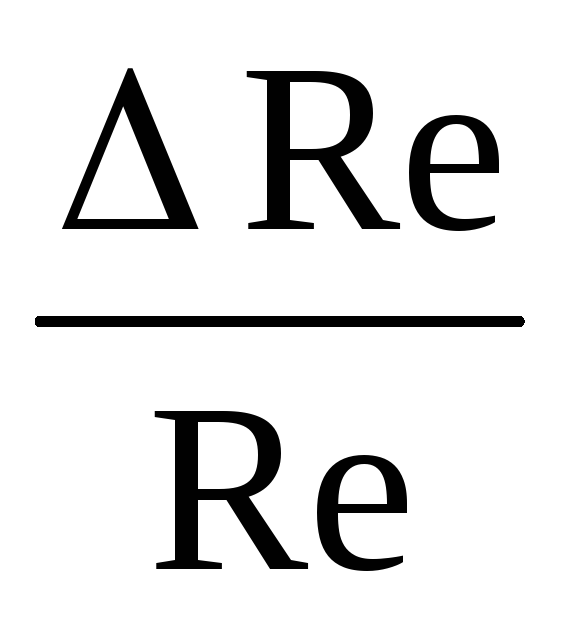Режимы движения жидкости.
Рядом исследователей еще в первой половине XIX века было замечено, что в потоке жидкости его частицы могут совершать движение по принципиально различным траекториям, и в соответствии с этим появилось понятие о существовании различных «режимов движения» жидкости.
В 1839-1854 г.г. немецким инженером-гидротехником Г. Хагеном было открыто существование двух принципиально разных режимов движения жидкости. В 1880 г. этот вопрос рассматривал Д.И. Менделеев.
Определенная ясность в этот вопрос была внесена английским физиком и инженером Осборном Рейнольдсом, который в 1883 г. опубликовал результаты своих наблюдений на лабораторной установке за водой, движущейся с различными скоростями в стеклянной трубке.
Опыты показали, что при малых скоростях движения воды, подкрашенная жидкость в виде тонкой струйки внутри ее не перемешивается с основным потоком. Такой режим получил название
После достижения определенной для данных условий опыта средней скорости движения, когда движение частиц жидкости приобретает как бы беспорядочный характер, струйка краски начинает размываться, отчего вся вода по сечению трубки окрашивается. Этот режим получил название турбулентного (от латинского слова turbulentus, означающего беспорядочный).
Опыты позволили
установить, что режим движения зависит
не только от скорости 
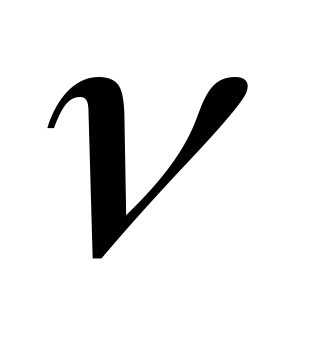 и диаметра трубыd.
и диаметра трубыd. Рейнольдс установил,
что критерием режима движения жидкости
является безразмерная величина, которая
впоследствии была названа его именем
– числом Рейнольдса 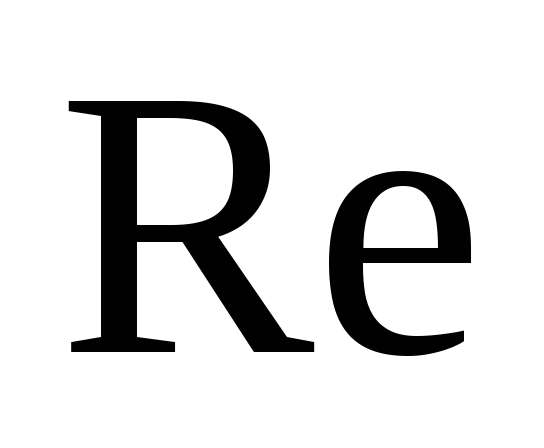 .
.
Для труб цилиндрического сечения число Рейнольдса определяется по формуле
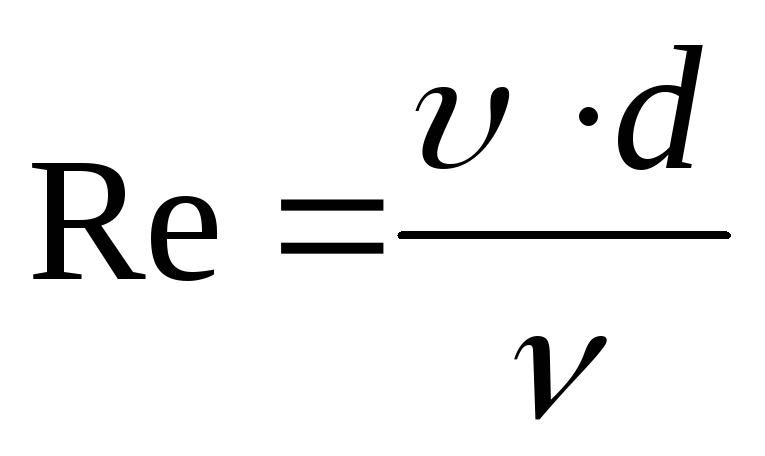 ,
(86)
,
(86)
где  — средняя скорость потока жидкости,
— средняя скорость потока жидкости,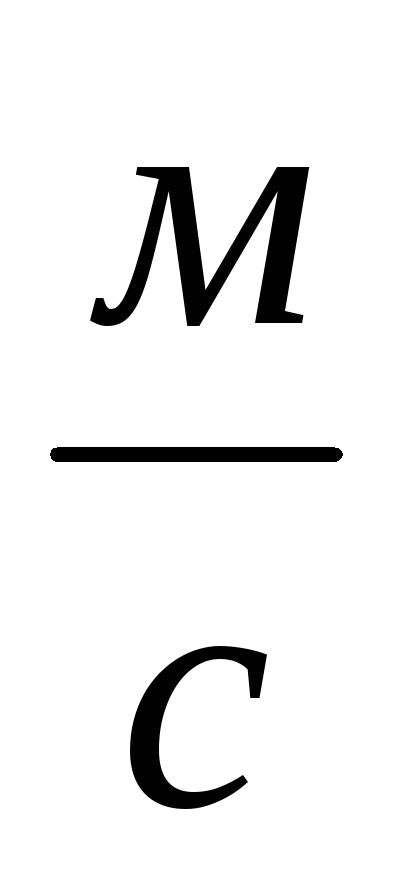 ;
;
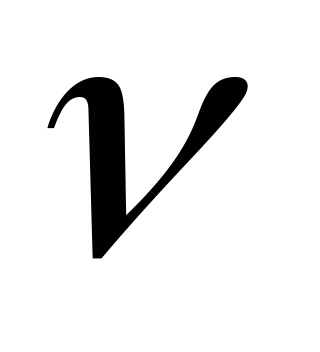 — коэффициент
кинематической вязкости жидкости,
— коэффициент
кинематической вязкости жидкости, 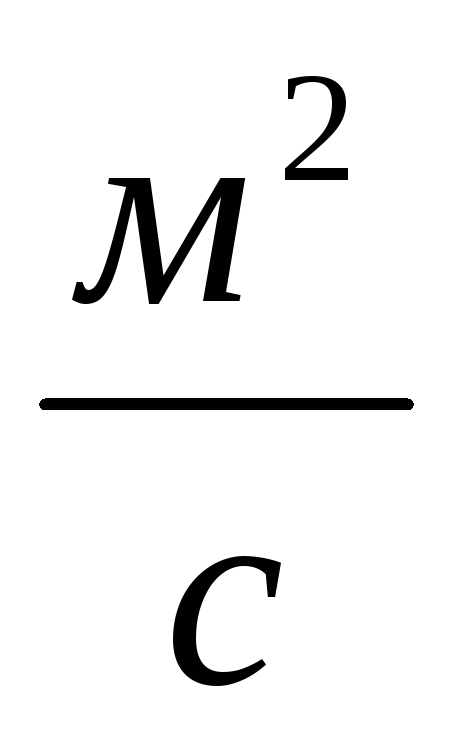 .
.
Критерий режима
движения, соответствующий нижней
критической скорости, называют нижним
критическим числом Рейнольдса. На
основании экспериментальных опытов
установлено, что нижнее критическое
число Рейнольдса для труб при напорном
движении 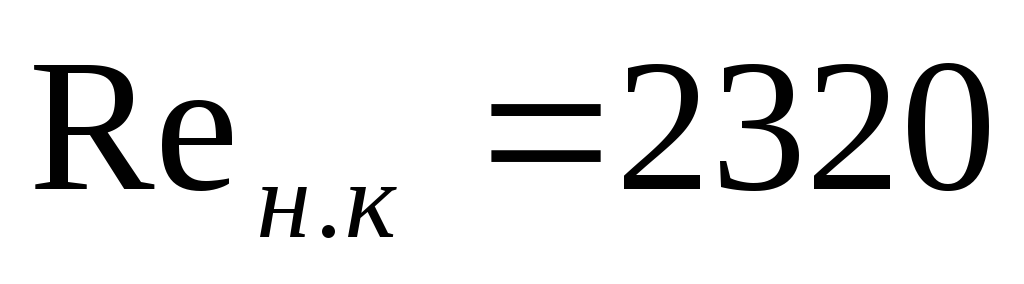
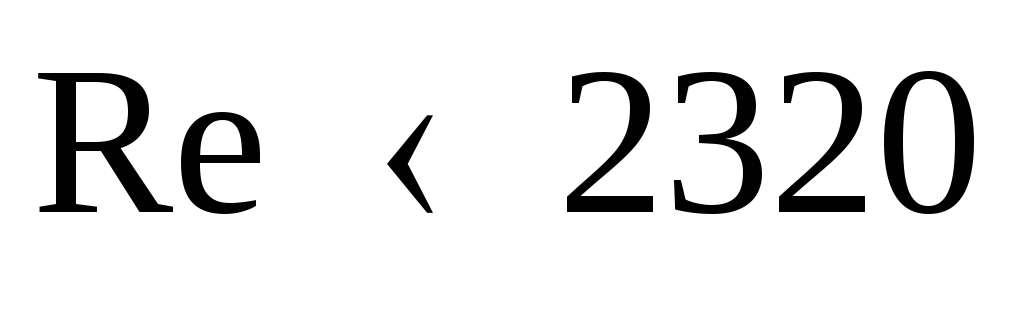 ,
то поток будет иметь ламинарный режим
движения, так как
,
то поток будет иметь ламинарный режим
движения, так как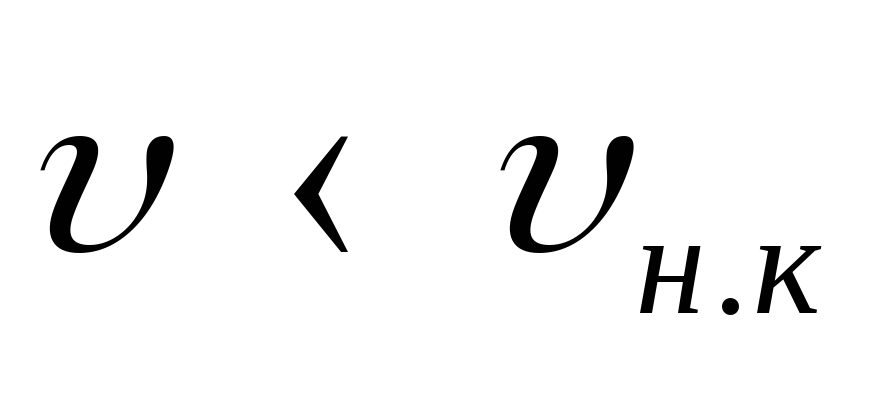 и режим находится в ламинарной зоне.
Если же
и режим находится в ламинарной зоне.
Если же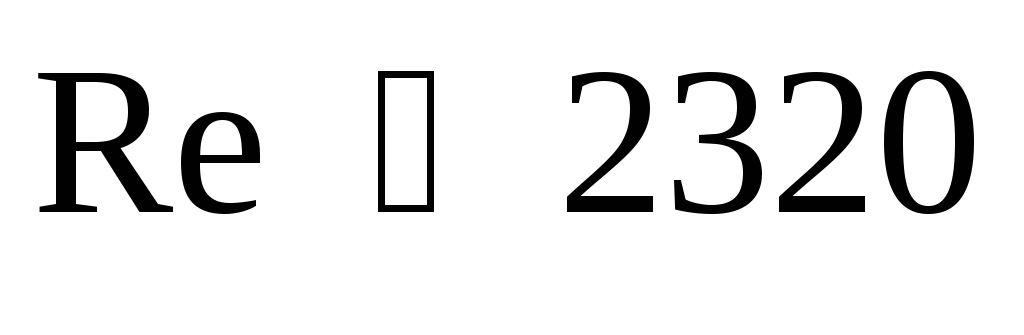 ,
то поток будет иметь либо турбулентный
режим, либо зону неустойчивого движения
(зона переходного режима), где Рейнольдс
может быть равным
,
то поток будет иметь либо турбулентный
режим, либо зону неустойчивого движения
(зона переходного режима), где Рейнольдс
может быть равным
С физической точки зрения критерий Рейнольдса есть отношение сил инерции потока к силам трения при его движении.
Определение режима движения жидкости в практических расчетах имеет очень важное значение. Опыты показали, что потери напора по длине потока при ламинарном режиме движения пропорциональны средне скорости течения в первой степени:
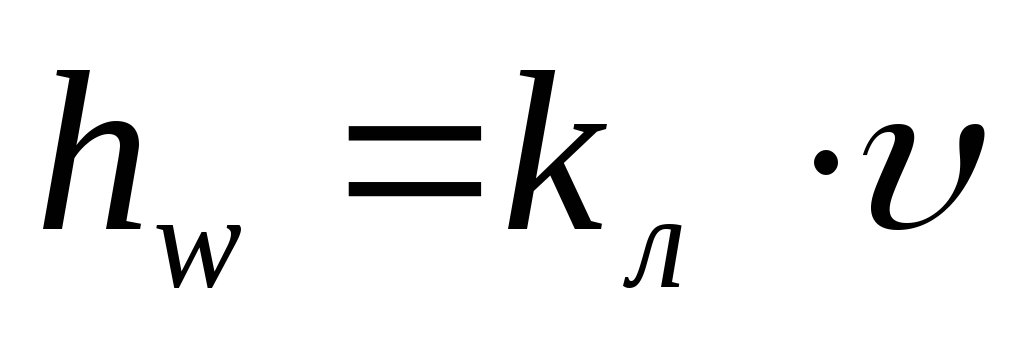
где |
| —
потери напора по длине потока, |
| — коэффициент пропорциональности; | |
| —
средняя скорость течения потока, |
Для турбулентного
режима движения потери напора по длине
потока пропорциональны средней скорости
течения в степени 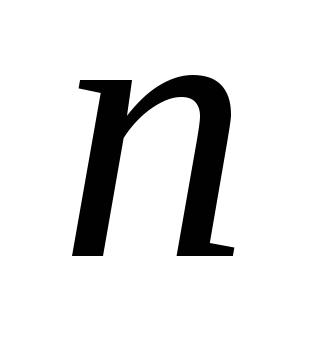 :
:
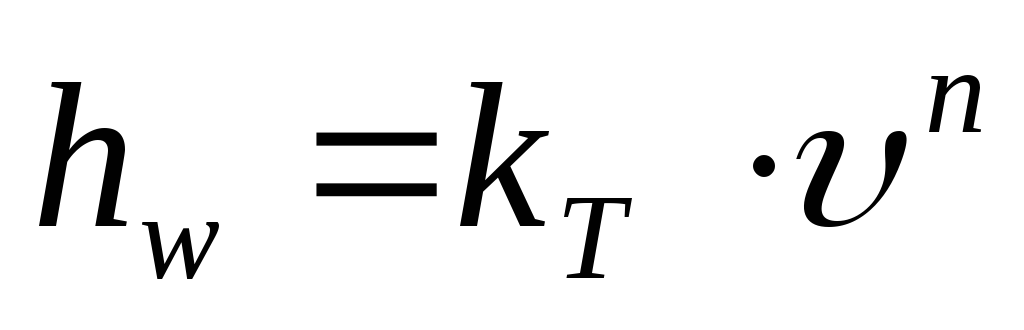
где | 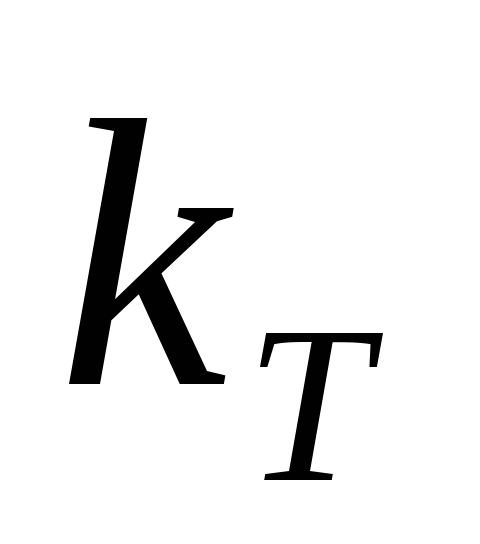 | — коэффициент пропорциональности; |
| — показатель степени, изменяющийся от 1,75 до 2. |
Экспериментальными исследованиями было установлено, что при турбулентном режиме движения жидкости основную часть потока по сечению составляет турбулентное ядро, а около стенок трубы существует пограничный слой, состоящий из тонкого ламинарного и тонкого переходного слоев (рис. 31).
Толщина ламинарного
слоя  определяется
по формуле
определяется
по формуле
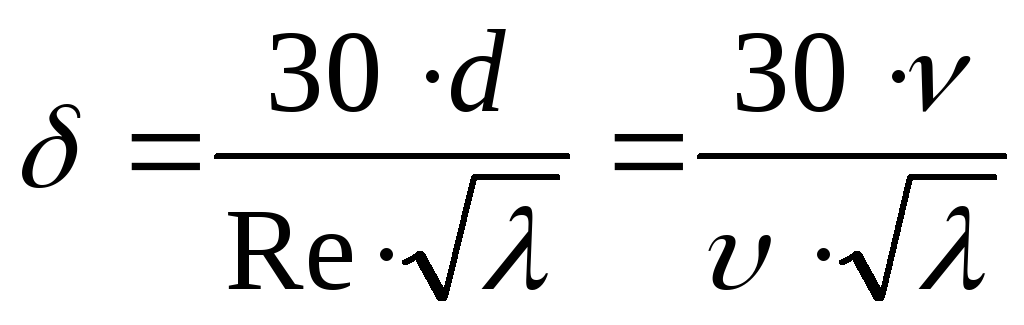 ,
(87)
,
(87)
где |
| —
толщина ламинарного слоя, |
| —
диаметр трубопровода, | |
| — число Рейнольдса; | |
| — коэффициент гидравлического трения; | |
| —
кинематический коэффициент вязкости, | |
| —
средняя скорость потока, |
Стенки труб имеют
шероховатость. В зависимости от
соотношения ламинарного слоя  и
высоты абсолютной шероховатости
и
высоты абсолютной шероховатости :
различают гидравлически гладкие трубы,
если
:
различают гидравлически гладкие трубы,
если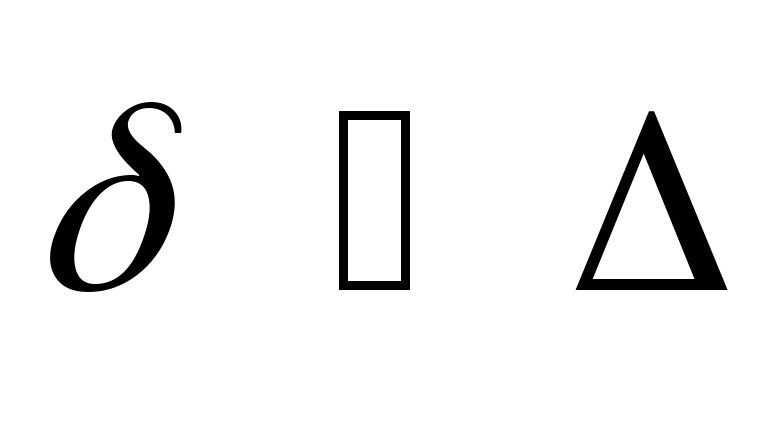 (рис.
31, б) и гидравлически шероховатые, если
(рис.
31, б) и гидравлически шероховатые, если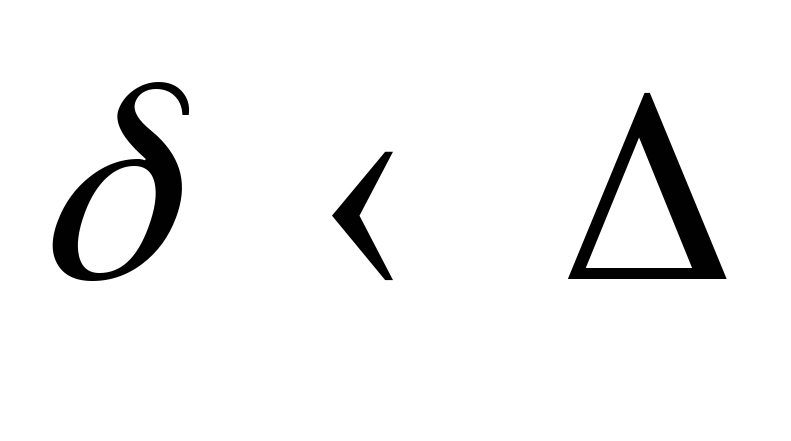 (рис. 31, в).
(рис. 31, в).
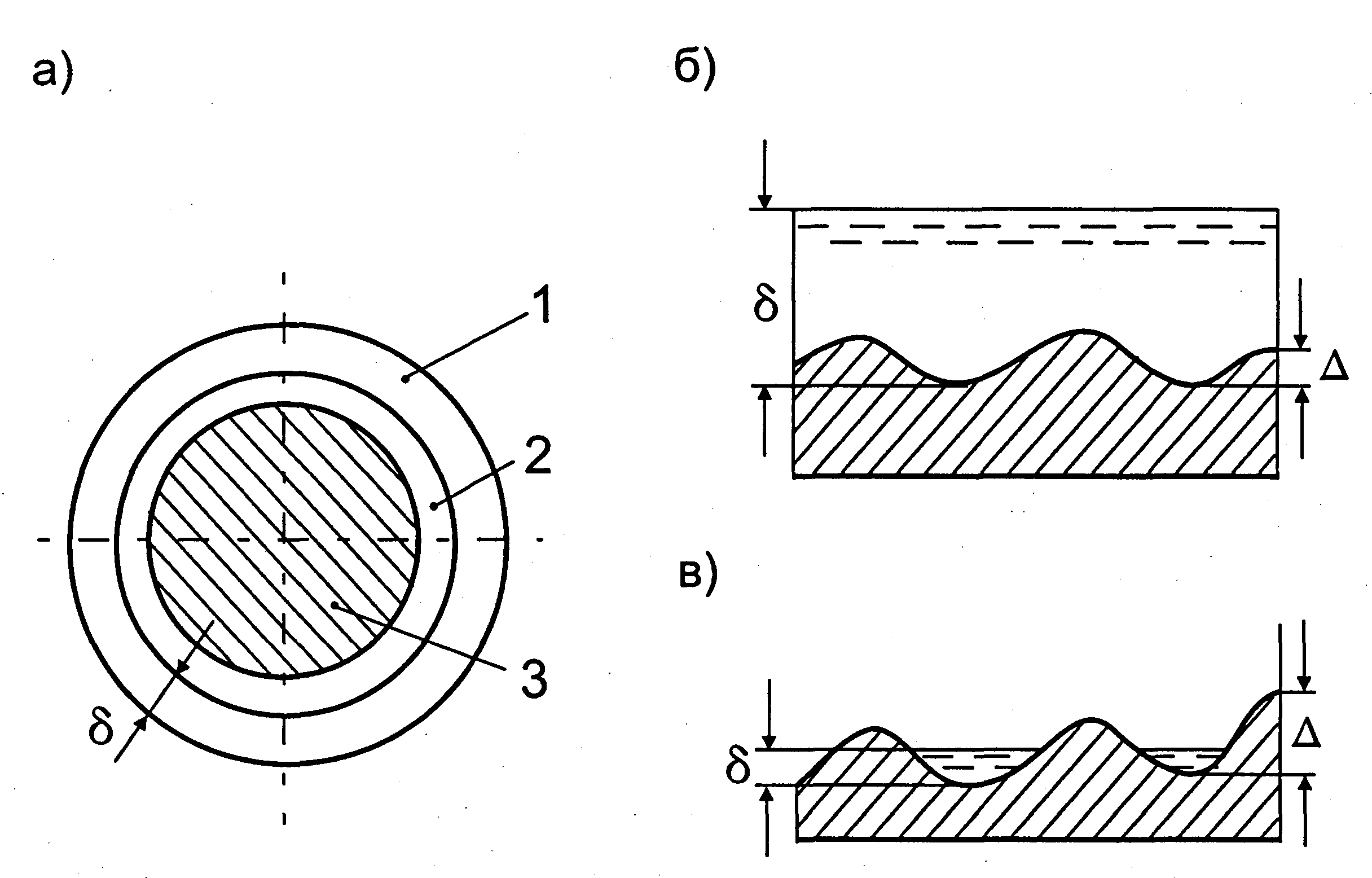
Рис. 31. Структура
турбулентного потока: а – пограничные
слои; б – гидравлически гладкая труба;
в – гидравлически шероховатая труба;
1 – ламинарный слой; 2 – переходный слой;
3 – турбулентное ядро;  — абсолютная шероховатость;
— абсолютная шероховатость; — толщина ламинарного слоя.
— толщина ламинарного слоя.
Так как фактическая
высота всех выступов шероховатости не
является одинаковой, то вводится понятие
эквивалентной шероховатости, которая
обозначается или 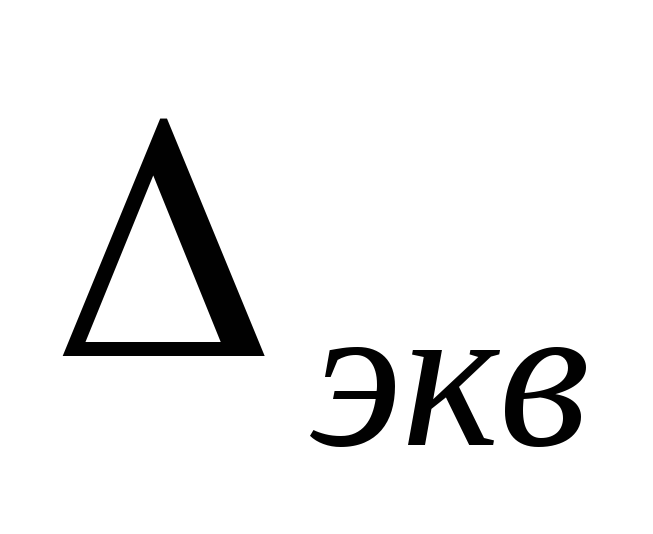 или
или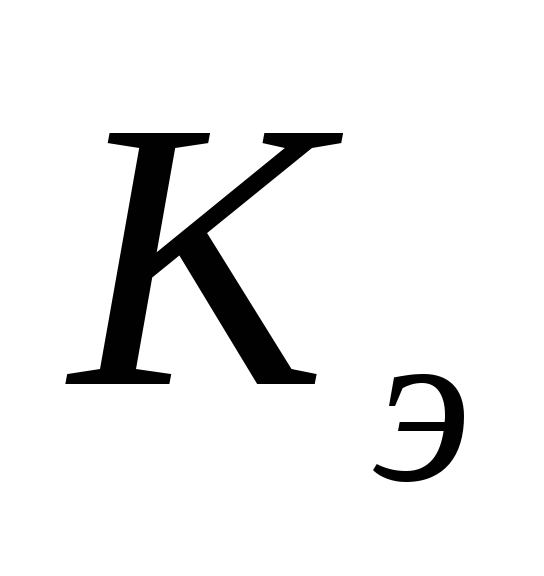 , т.е. такая равномерная шероховатость,
которая дает при подсчете одинаковую
с заданной шероховатостью величину
потерь напора по длине
, т.е. такая равномерная шероховатость,
которая дает при подсчете одинаковую
с заданной шероховатостью величину
потерь напора по длине 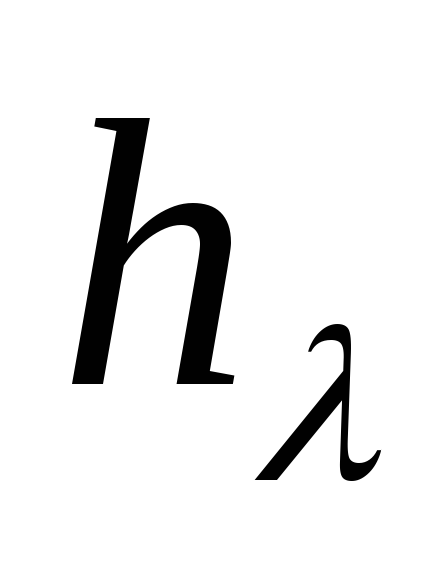 .
.
Шероховатость
обычно характеризуется не высотой
выступов шероховатости  ,
а отношением
,
а отношением к радиусу или диаметру трубопровода,
т.е.
к радиусу или диаметру трубопровода,
т.е. или
или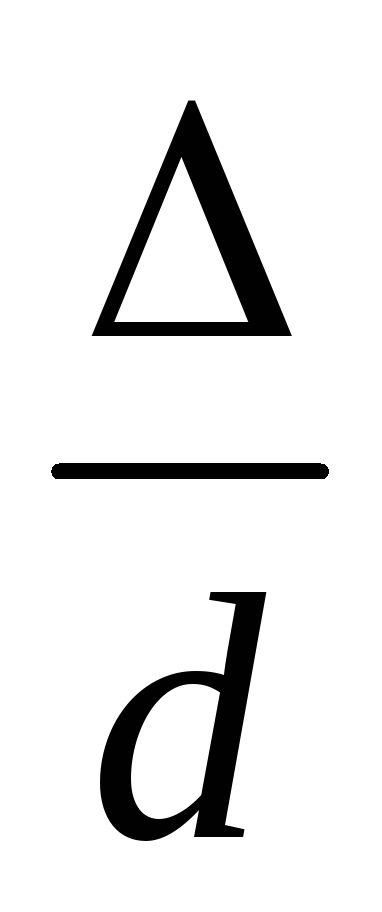 ,
и называетсяотносительной
шероховатостью.
,
и называетсяотносительной
шероховатостью.
Следует заметить, что при различных числах Рейнольдса одна и та же труба может быть как гладкой, так и шероховатой.
Ниже приведены
численные значения эквивалентной
шероховатости для некоторых поверхностей,  .
.
Стеклянные трубы | 0,005 | |
Цельнотянутые металлические трубы: латунные новые стальные стальные находящиеся в эксплуатации | 0,005 0,02 1,2 | |
Цельносварные трубы новые бывшие в эксплуатации сильно корродированные | 0,04 0,1 2,0 | |
Чугунные трубы: новые бывшие в эксплуатации | 0,25 1,0 | |
Бетонные трубы: с хорошей затиркой среднего качества затирки | 0,3 2,5 | |
Асбоцементные трубы новые бывшие в эксплуатации | 0,05 0,6 | |
Деревянные поверхности из тщательно остроганных досок тоже из хорошо отстроганных досок | 0,15 0,3 |
studfile.net
Режимы движения вязких жидкостей
Существует ламинарный и турбулентный режимы движения. При медленном движении жидкости в прямолинейном трубопроводе движение является ламинарным.
При ламинарном течении слои жидкости скользят друг по другу, не перемешиваясь. С увеличением скорости в отдельных слоях образуются вихри, за счет чего слои жидкости перемешиваются. Такое движение называется турбулентным. Ученый Рейнольдс провел опыт, в котором струи жидкости в трубе были окрашенными.
Он установил, что при увеличении скорости течения, диаметра трубки и плотности жидкости, а также при уменьшении её вязкости до определенного критического значения, ламинарный режим переходит в турбулентный. Рейнольдс получил количественную характеристику, которая была названа критерием Рейнольдса
 (3.3)
(3.3)
где 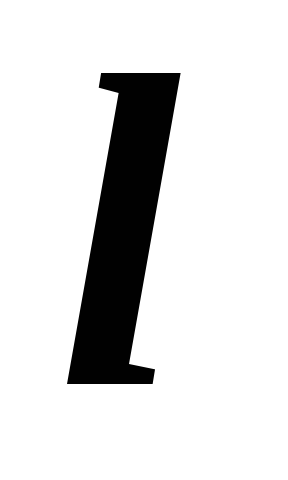 ─ характерный линейный размер, или
─ характерный линейный размер, или ─ диаметр круглой трубы.
─ диаметр круглой трубы.
Для
некруглой трубы 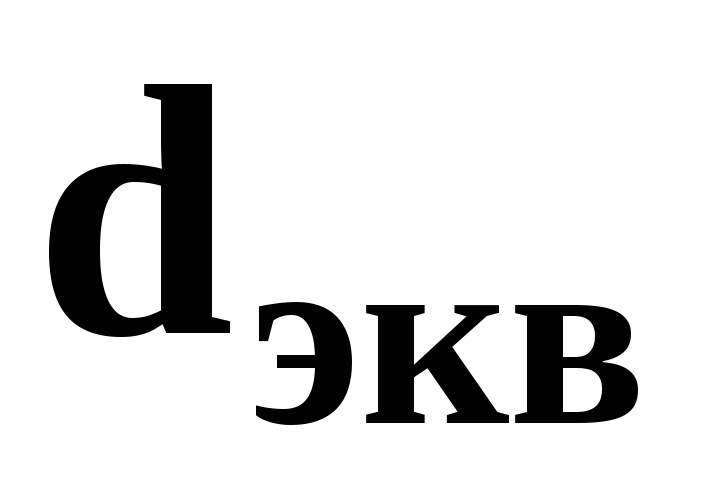 ─ эквивалентный диаметр.
─ эквивалентный диаметр.
Так
как 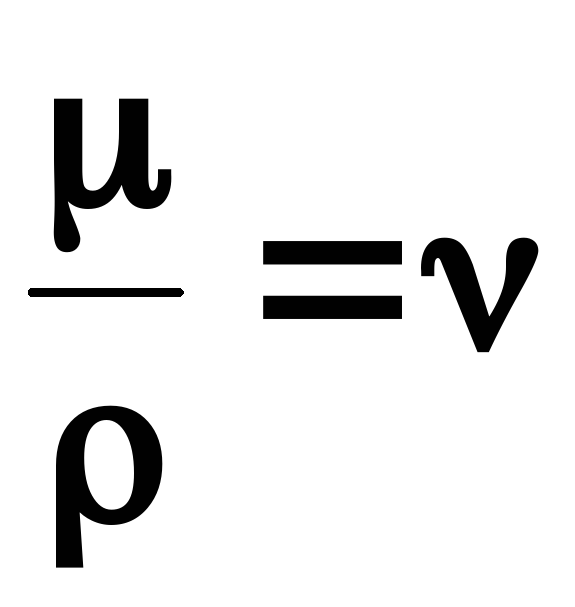 ─ кинематическая вязкость, то критерий
Рейнольдса можно записать
─ кинематическая вязкость, то критерий
Рейнольдса можно записать
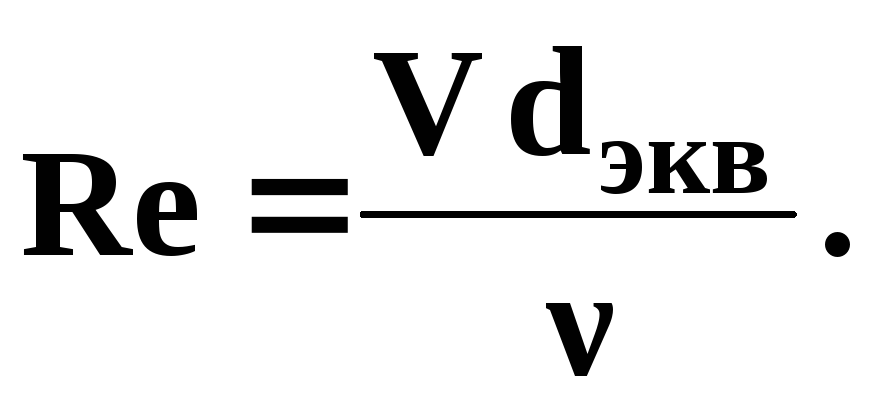 (3.4)
(3.4)
Критерий Рейнольдса является безразмерной величиной.
Экспериментально
установлено, что ламинарный поток в
трубе сохраняется до 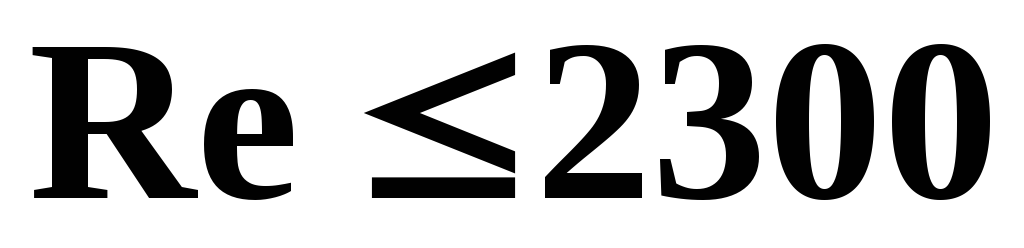 ,
а при
,
а при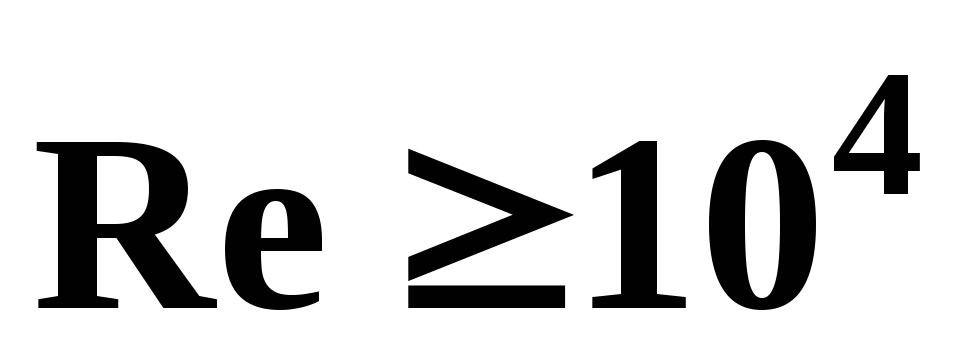 устанавливается турбулентный режим,
между 2300 и 104 ─ переходный режим.
устанавливается турбулентный режим,
между 2300 и 104 ─ переходный режим.
Значение
числа Рейнольдса для труб круглого
поперечного сечения, равное 2300,
называется критическим, т.е. 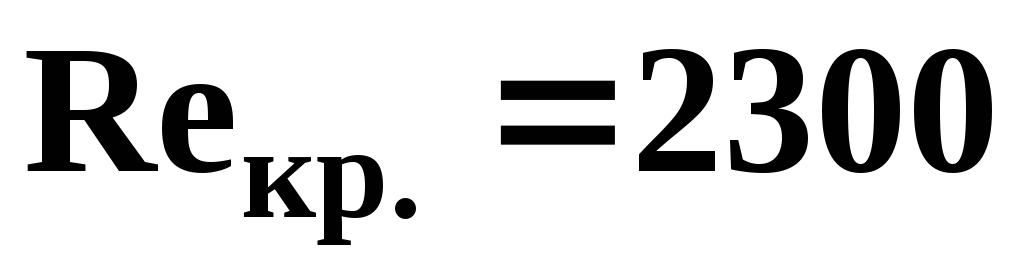 .
.
Уравнение неразрывности
И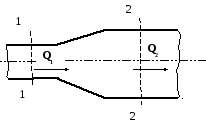 з
закона сохранения вещества и постоянства
расхода вытекаетуравнение
неразрывности течений. Представим трубу с переменным
живым сечением (рисунок 3.3).
з
закона сохранения вещества и постоянства
расхода вытекаетуравнение
неразрывности течений. Представим трубу с переменным
живым сечением (рисунок 3.3).
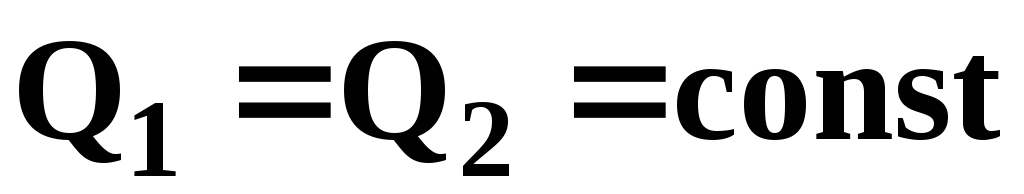
Рисунок 3.3 ─ Труба с переменным диаметром при постоянном расходе
Расход
жидкости через трубу в любом ее сечении
постоянен, т.е. 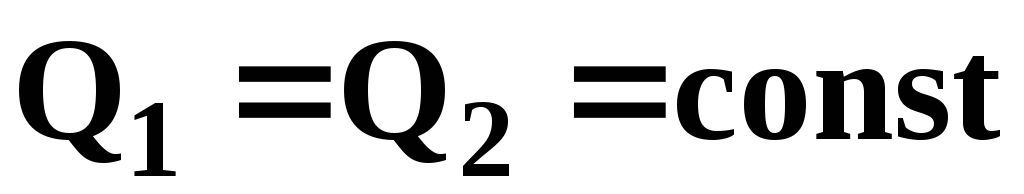 откуда
откуда
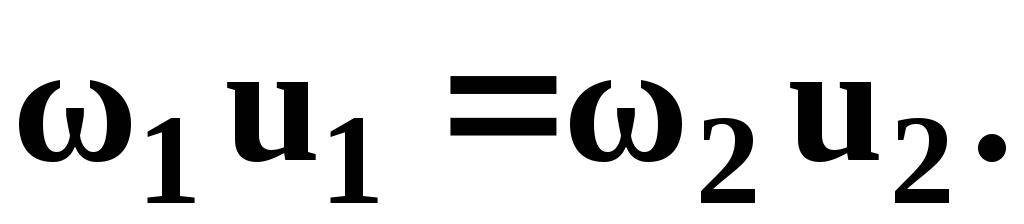
Таким образом, если течение в трубе является сплошным и неразрывным, то уравнение неразрывности примет вид:
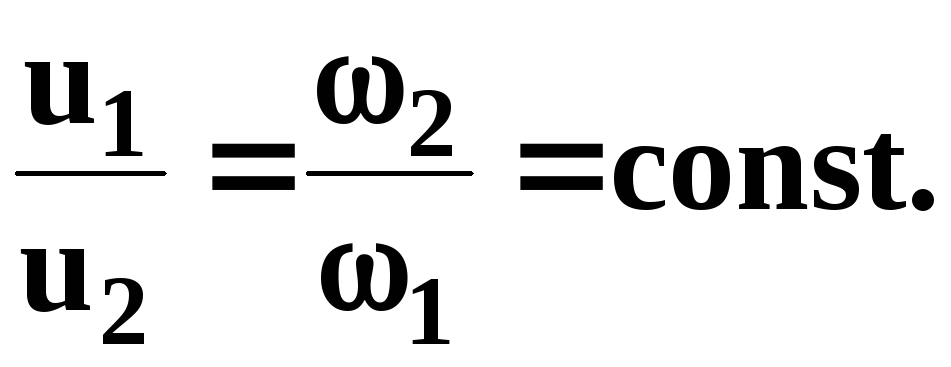 (3.5)
(3.5)
Уравнение Бернулли для идеальной жидкости
Уравнение Даниила Бернулли, полученное в 1738 г., является фундаментальным уравнением гидродинамики. Оно дает связь между давлением р, средней скоростью υ и пьезометрической высотой z в различных сечениях потока и выражает закон сохранения энергии движущейся жидкости. С помощью этого уравнения решается большой круг задач.
Рассмотрим трубопровод переменного диаметра, расположенный в пространстве под углом β (рисунок 3.4).
Выберем произвольно на рассматриваемом участке трубопровода два сечения: сечение 1-1 и сечение 2-2. Вверх по трубопроводу от первого сечения ко второму движется жидкость, расход которой равен Q.
Для
измерения давления жидкости применяют пьезометры ─ тонкостенные стеклянные трубки, в
которых жидкость поднимается на высоту 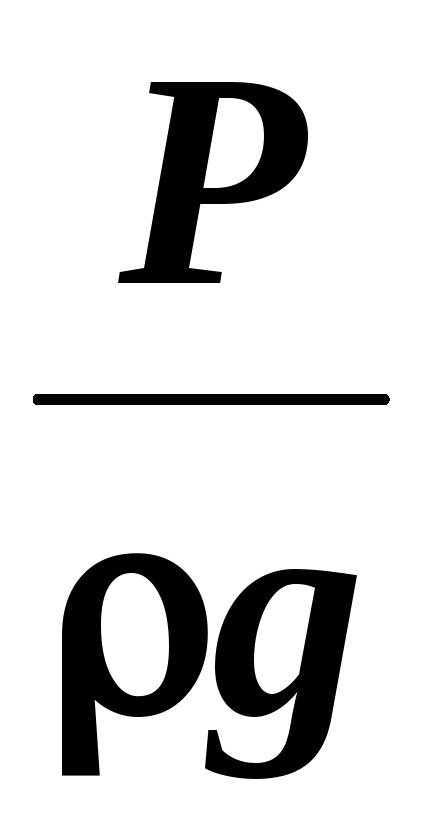 .
В каждом сечении установлены пьезометры,
в которых уровень жидкости поднимается
на разные высоты.
.
В каждом сечении установлены пьезометры,
в которых уровень жидкости поднимается
на разные высоты.
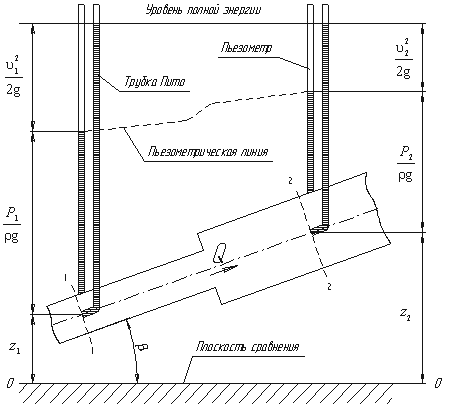
Рисунок 3.4 ─ Схема к выводу уравнения Бернулли для
идеальной жидкости
Кроме пьезометров в каждом сечении 1-1 и 2-2 установлена трубка, загнутый конец которой направлен навстречу потоку жидкости, которая называется трубка Пито. Жидкость в трубках Пито также поднимается на разные уровни, если отсчитывать их от пьезометрической линии.
Пьезометрическую линию можно построить следующим образом. Если между сечением 1-1 и 2-2 поставить несколько таких же пьезометров и через показания уровней жидкости в них провести кривую, то мы получим ломаную линию (рисунок 3.4).
Однако высота уровней в трубках Пито относительно произвольной горизонтальной прямой 0-0, называемой плоскостью сравнения, будет одинакова.
Если через показания уровней жидкости в трубках Пито провести линию, то она будет горизонтальна, и будет отражать уровень полной энергии трубопровода.
Для двух произвольных сечений 1-1 и 2-2 потока идеальной жидкости уравнение Бернулли имеет следующий вид:
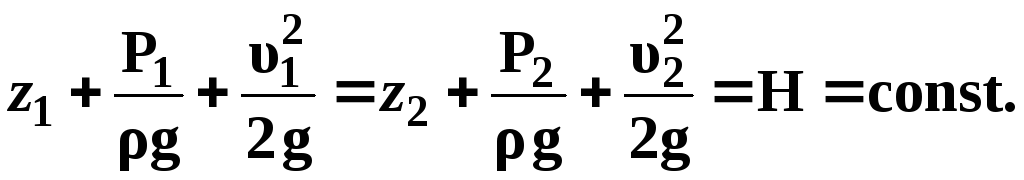 (3.6)
(3.6)
Так как сечения 1-1 и 2-2 взяты произвольно, то полученное уравнение можно переписать иначе:
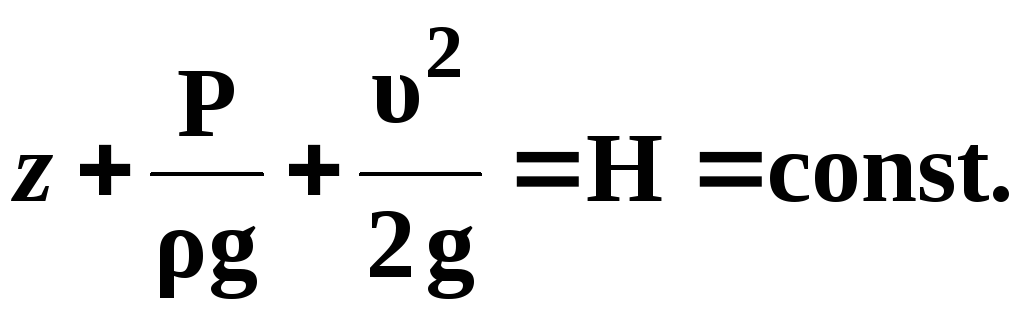 (3.7)
(3.7)
и прочитать так: сумма трех членов уравнения Бернулли для любого сечения потока идеальной жидкости есть величина постоянная.
С энергетической точки зрения каждый член уравнения представляет собой определенные виды энергии:
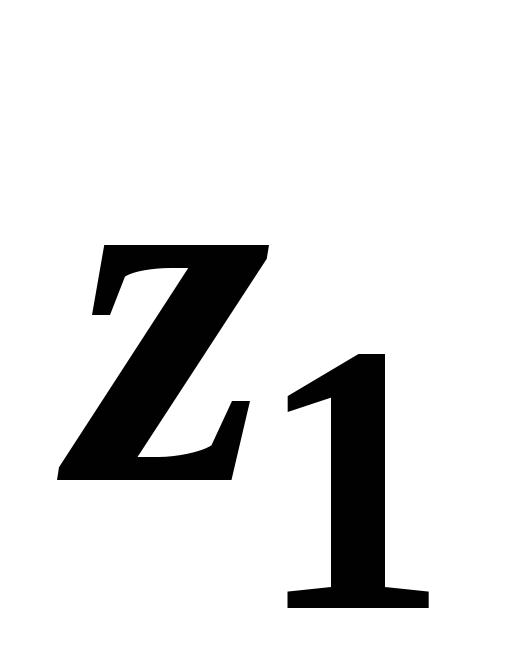 и
и 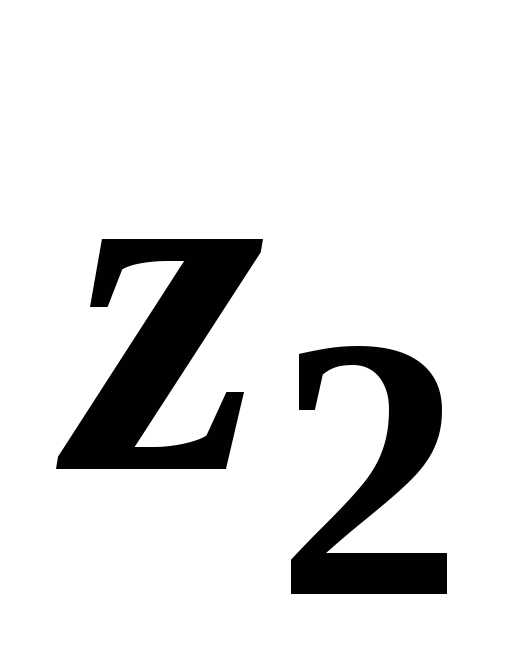 ─ удельные энергии положения,
характеризующие потенциальную энергию
в сечениях1-1 и 2-2;
─ удельные энергии положения,
характеризующие потенциальную энергию
в сечениях1-1 и 2-2;
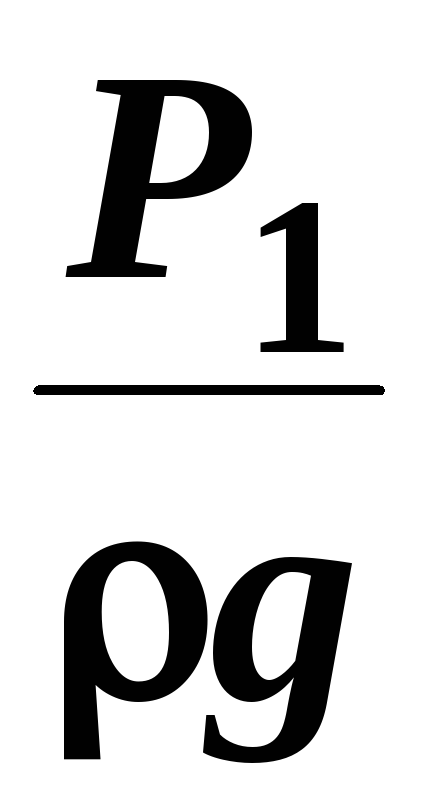 и
и 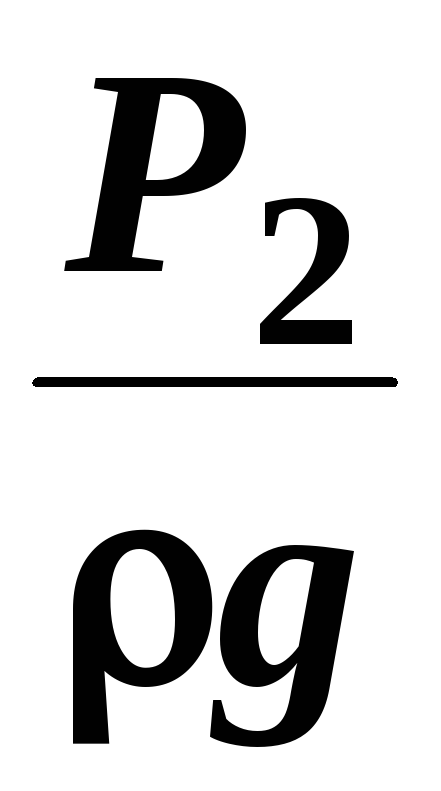 ─ удельные энергии давления, характеризующие
потенциальную энергию давления в тех
же сечениях;
─ удельные энергии давления, характеризующие
потенциальную энергию давления в тех
же сечениях;
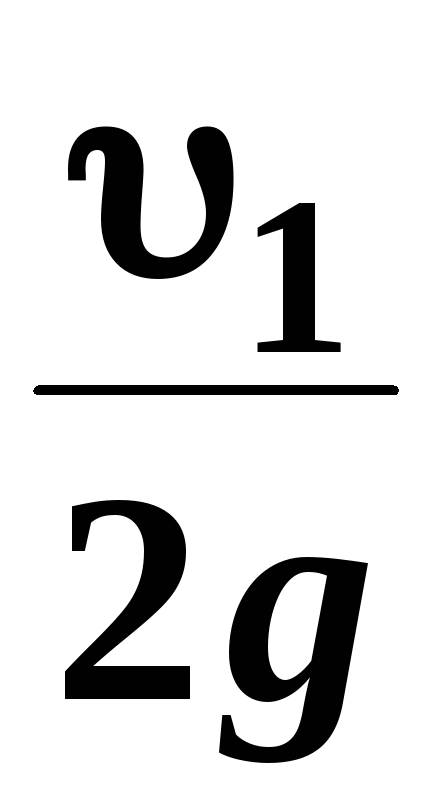 и
и 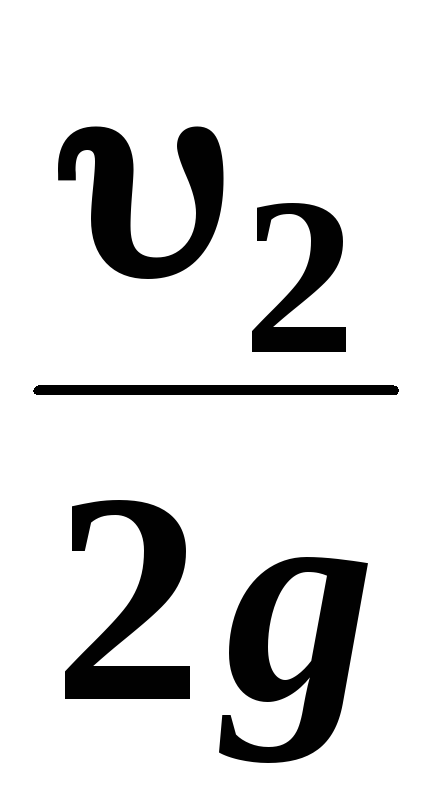 ─ удельные кинетические энергии в тех
же сечениях.
─ удельные кинетические энергии в тех
же сечениях.
Следовательно, согласно уравнению Бернулли, полная удельная энергия идеальной жидкости в любом сечении постоянна.
Уравнение
Бернулли можно истолковать и чисто
геометрически. Дело в том, что каждый
член уравнения имеет линейную размерность.
Глядя на рисунок 3.6, можно заметить, что 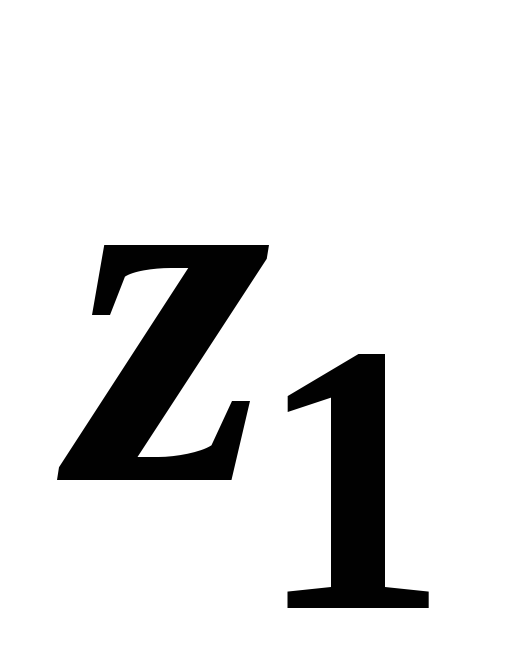 и
и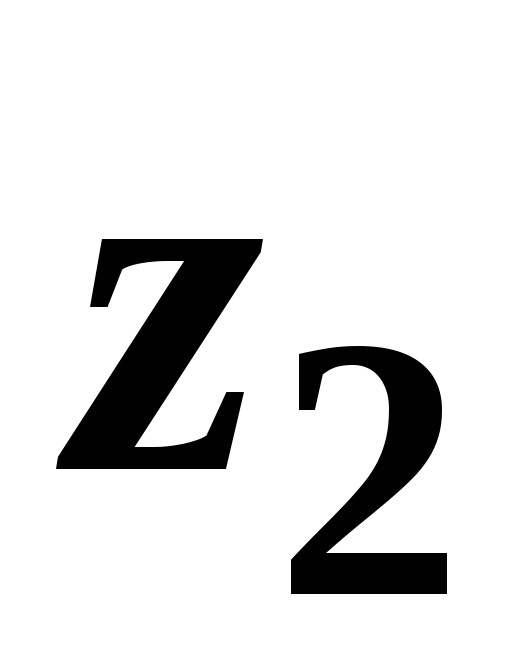 ─ геометрические высоты сечений1-1 и 2-2 над плоскостью сравнения;
─ геометрические высоты сечений1-1 и 2-2 над плоскостью сравнения;
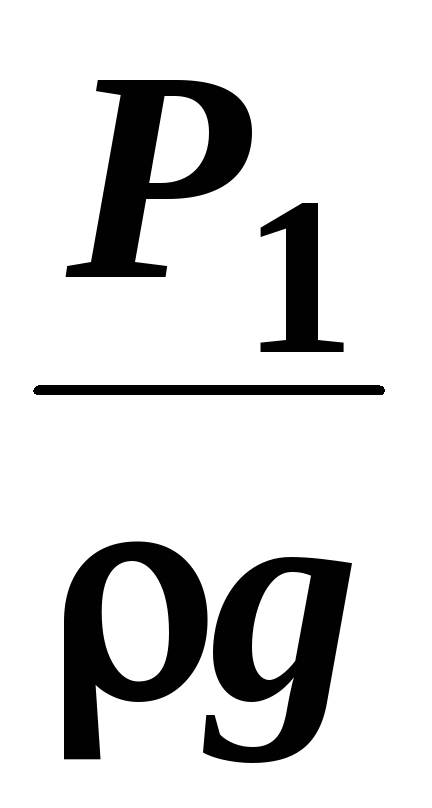 и
и 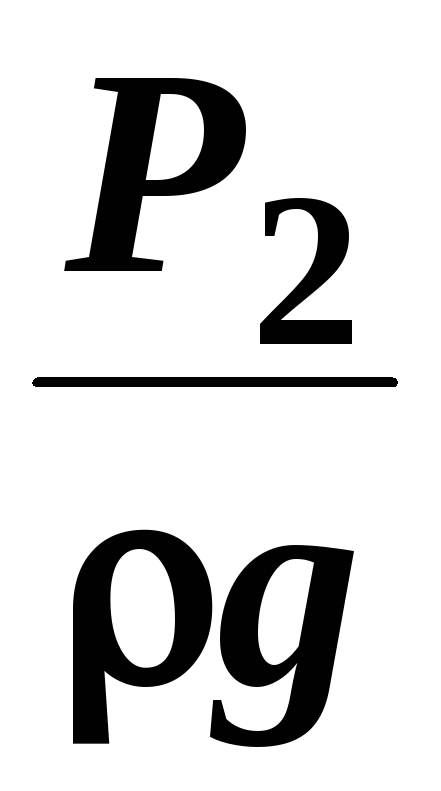 ─
пьезометрические высоты;
─
пьезометрические высоты;
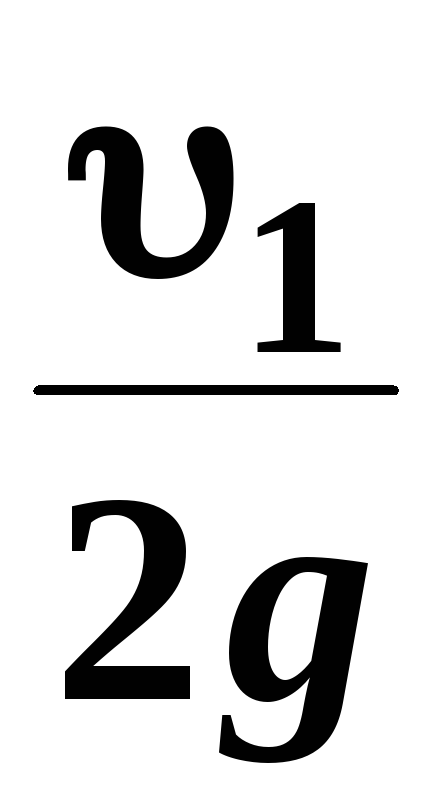 и
и 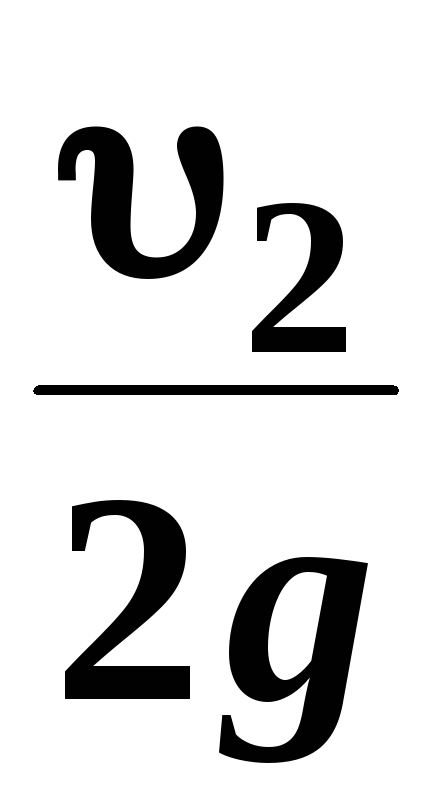 ─ скоростные высоты в указанных сечениях.
─ скоростные высоты в указанных сечениях.
В этом случае уравнение Бернулли можно прочитать так: сумма геометрической, пьезометрической и скоростной высоты для идеальной жидкости есть величина постоянная.
studfile.net
Ламинарный Режим движения жидкости
Ламинарным течением жидкости называется слоистое течение без перемешивания частиц жидкости и без пульсаций скоростей и давления.
З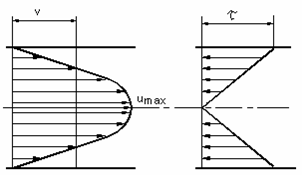 акон
распределения скоростей по сечению
круглой трубы при ламинарном режиме
движения, установленный английским
физиком Дж. Стоксом, имеет вид
акон
распределения скоростей по сечению
круглой трубы при ламинарном режиме
движения, установленный английским
физиком Дж. Стоксом, имеет вид
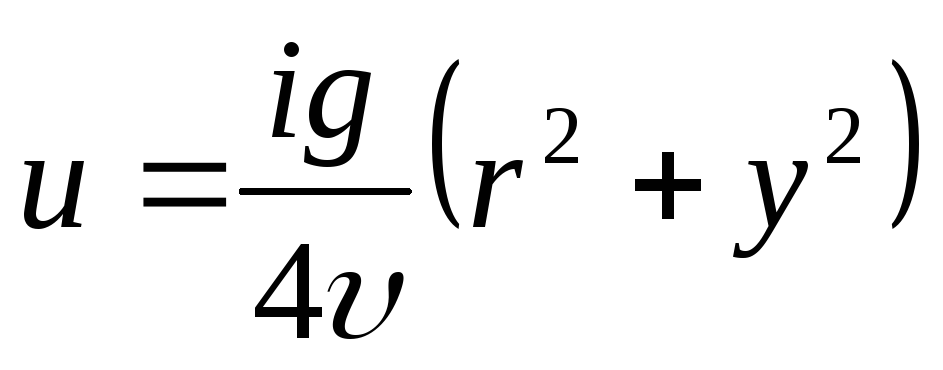 ,
,
где 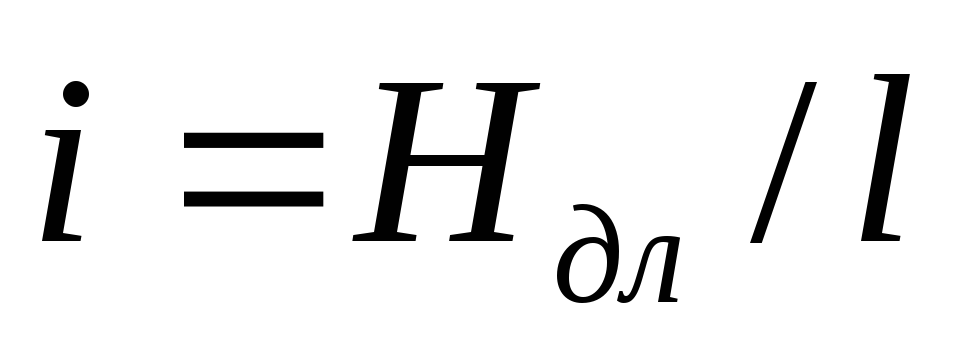 ,
,
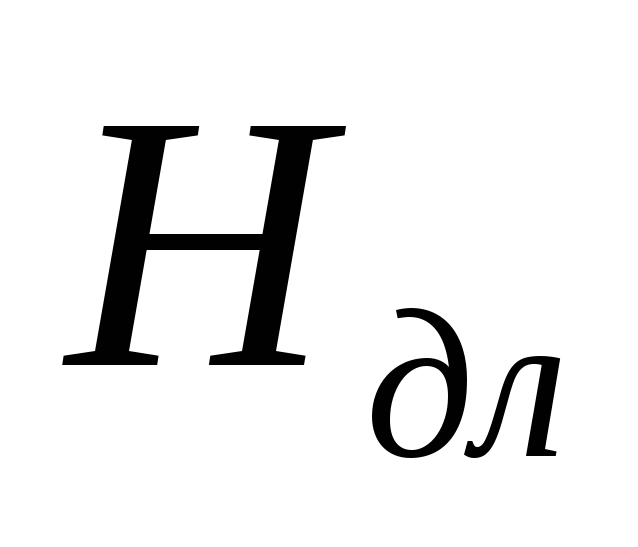 —
потери напора по длине.
—
потери напора по длине.
При 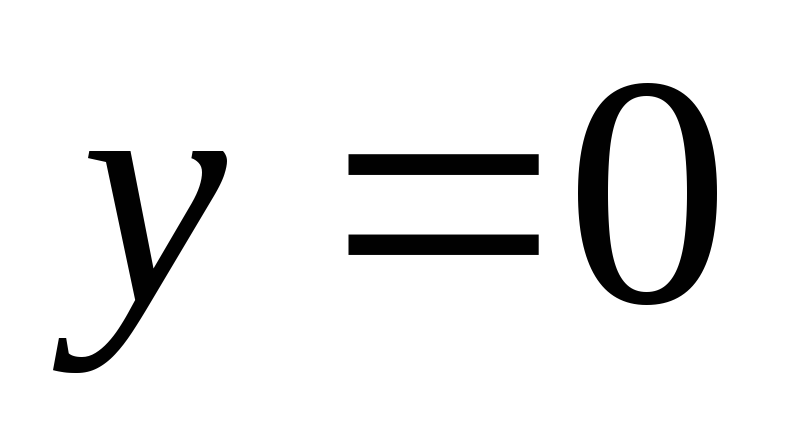 ,
т.е. на оси трубы
,
т.е. на оси трубы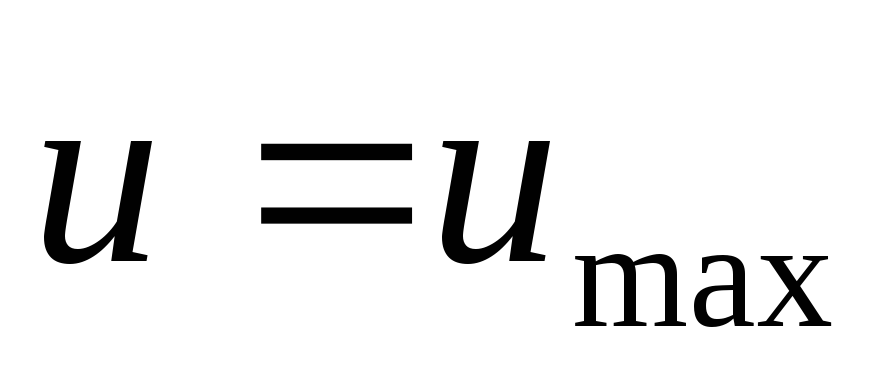 ,
,
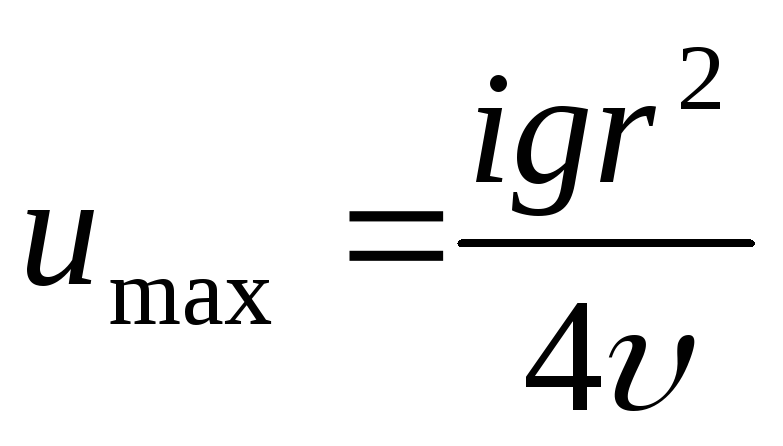 .
.
При ламинарном движении эпюра скоростей по поперечному сечению трубы будет иметь форму квадратичной параболы.
Турбулентный Режим движения жидкости
Турбулентным называется течение, сопровождающееся интенсивным перемешиванием жидкости и пульсациями скоростей и давлений.
В результате наличия вихрей и интенсивного перемешивания частиц жидкости в любой точке турбулентного потока в данный момент времени имеет место своя по значению и направлению мгновенная местная скорость u, а траектория частиц, проходящих через эту точку, имеет различный вид (занимают разное положение в пространстве и имеют различную форму). Такое колебание во времени мгновенной местной скорости называется пульсацией скорости. То же происходит и с давлением. Таким образом, турбулентное движение является неустановившимся.
Усредненная местная скорость ū – фиктивной средней скорости в данной точке потока на достаточно длительный промежуток времени, которая несмотря на значительные колебания мгновенных скоростей, остается практически постоянной по значению и параллельной оси потоков
| |
П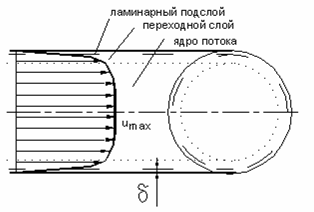 о
Прандтлю турбулентный поток состоит
из двух областей:ламинарного
подслоя и турбулентного
ядра потока,
между которыми существует еще одна
область – переходной
слой.
Совокупность ламинарного подслоя и
переходного слоя в гидродинамике
называют обычно пограничным
слоем.
о
Прандтлю турбулентный поток состоит
из двух областей:ламинарного
подслоя и турбулентного
ядра потока,
между которыми существует еще одна
область – переходной
слой.
Совокупность ламинарного подслоя и
переходного слоя в гидродинамике
называют обычно пограничным
слоем.
Ламинарный подслой, расположенный непосредственно у стенок трубы, имеет весьма малую толщину δ, которая может быть определена по формуле
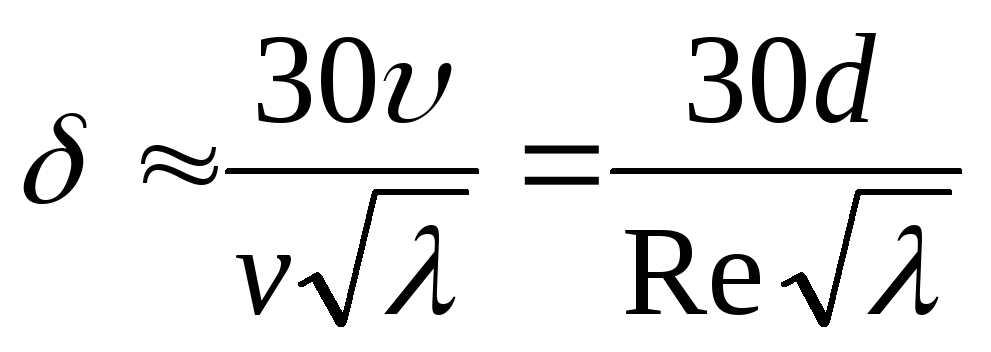 .
.
В переходном слое ламинарное течение уже нарушается поперечным перемещением частиц, причем чем дальше расположена точка от стенки трубы, тем выше интенсивность перемешивания частиц. Толщина этого слоя также невелика, но четкую его границу установить трудно.
Основную часть живого сечения потока занимает ядро потока, в котором наблюдается интенсивное перемешивание частиц, поэтому именно оно характеризует турбулентное движение потока в целом.
ПОНЯТИЕ О ГИДРАВЛИЧЕСКИ ГЛАДКИХ И ШЕРОХОВАТЫХ ТРУБАХ
П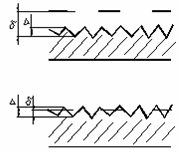 оверхность
стенок труб, каналов, лотков имеют ту
или иную шероховатость. Обозначим высоту
выступов шероховатости буквой Δ. Величину
Δ называютабсолютной
шероховатостью,
а ее отношение к диаметру трубы (Δ/d)
— относительной
шероховатостью;
величина обратная относительной
шероховатости, носит название относительной
гладкости (d/Δ).
оверхность
стенок труб, каналов, лотков имеют ту
или иную шероховатость. Обозначим высоту
выступов шероховатости буквой Δ. Величину
Δ называютабсолютной
шероховатостью,
а ее отношение к диаметру трубы (Δ/d)
— относительной
шероховатостью;
величина обратная относительной
шероховатости, носит название относительной
гладкости (d/Δ).
В зависимости от соотношения толщены ламинарного подслоя δ и высоты выступов шероховатости Δ различают гидравлически гладкие и шероховатые трубы. Если ламинарный подслой полностью покрывает все выступы на стенках трубы, т.е. δ>Δ, трубы считаются гидравлически гладкими. При δ<Δ трубы считаются гидравлически шероховатыми. Так как значение δ зависит от Re, то одна и та же труба может быть в одних и тех же условиях гидравлически гладкой (при малых Re), а в других – шероховатой (при больших Re).
Лекция №9
ГИДРАВЛИЧЕСКИЕ ПОТЕРИ
ОБЩИЕ СВЕДЕНИЯ.
При движении потока реальной жидкости происходят потери напора, так как часть удельной энергии потока затрачивается на преодоление различных гидравлических сопротивлений. Количественное определение потерь напора hп является одной из важнейших задач гидродинамики, без решения которой не возможно практическое использование уравнения Бернулли:
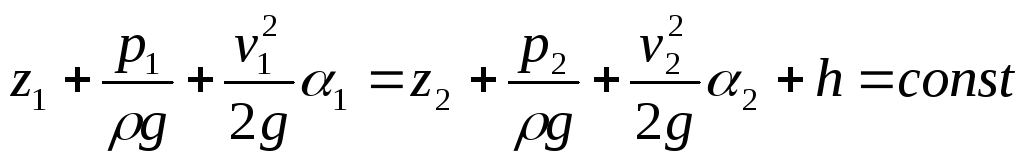 ,
,
где α – коэффициент кинетической энергии, равный для турбулентного потока 1,13, а для ламинарного — 2; v -средняя скорость потока; h — уменьшение удельной механической энергии потока на участке между сечениями 1 и 2, проходящее в результате сил внутреннего трения.
Потери удельной энергии (напора), или, как их часто называют, гидравлические потери, зависят от формы, размеров русла, скорости течения и вязкости жидкости, а иногда и от абсолютного давления в ней. Вязкость жидкости, хотя и является первопричиной всех гидравлических потерь, но далеко не всегда оказывает существенное влияние на их величину.
Как показывают опыты, во многих, но не во всех случаях гидравлические потери приблизительно пропорциональны скорости течения жидкости во второй степени, поэтому в гидравлике принят следующий общий способ выражения гидравлических потерь полного напора в линейных единицах:
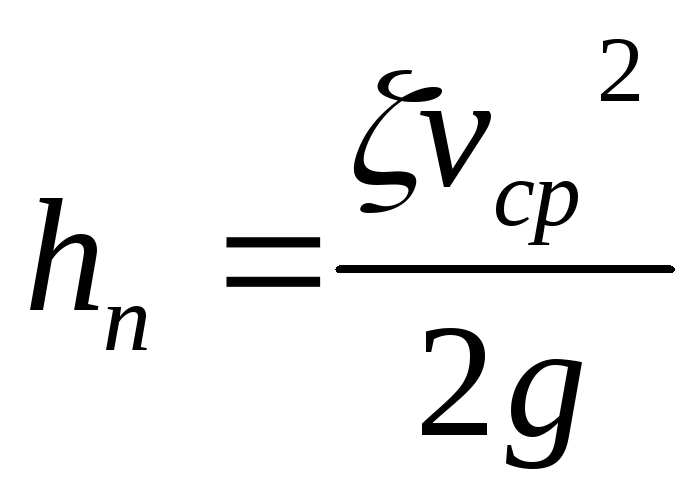 ,
,
или в единицах давления
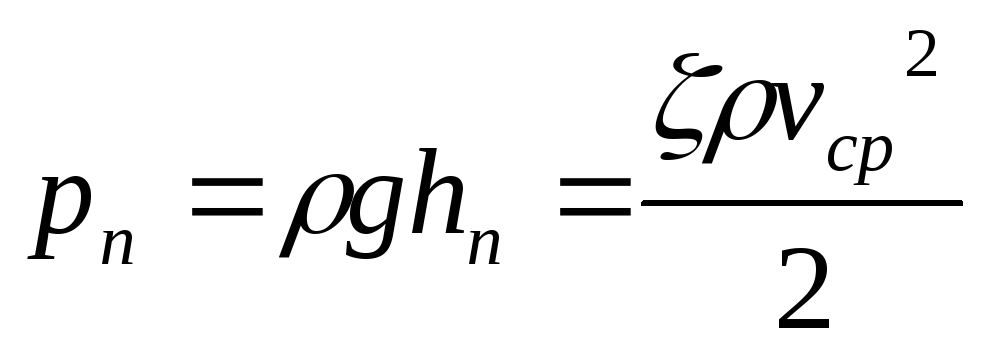 .
.
Такое выражение удобно тем, что включает в себя безразмерный коэффициент пропорциональности ζ называемый коэффициентом потерь, или коэффициентом сопротивления, значение которого для данного русла в первом грубом приближении постоянно.
Коэффициент потерь ζ, таким образом, есть отношение потерянного напора к скоростному напору.
Гидравлические потери обычно разделяют на местные потери и потери на трение по длине.
М естные
потериэнергии
обусловлены так называемыми местными
гидравлическими сопротивлениями, т.е.
местными изменениями формы и размера
русла, вызывающими деформацию потока.
При протекании жидкости через местные
сопротивления изменяется ее скорость
и обычно возникают крупные вихри.
Последние образуются за местом отрыва
потока от стенок и представляют собой
области, в которых частицы жидкости
движутся в основном по замкнутым кривым
или близким к ним траекториям.
естные
потериэнергии
обусловлены так называемыми местными
гидравлическими сопротивлениями, т.е.
местными изменениями формы и размера
русла, вызывающими деформацию потока.
При протекании жидкости через местные
сопротивления изменяется ее скорость
и обычно возникают крупные вихри.
Последние образуются за местом отрыва
потока от стенок и представляют собой
области, в которых частицы жидкости
движутся в основном по замкнутым кривым
или близким к ним траекториям.
Местные потери напора определяются по формуле Вейсбаха следующим образом:
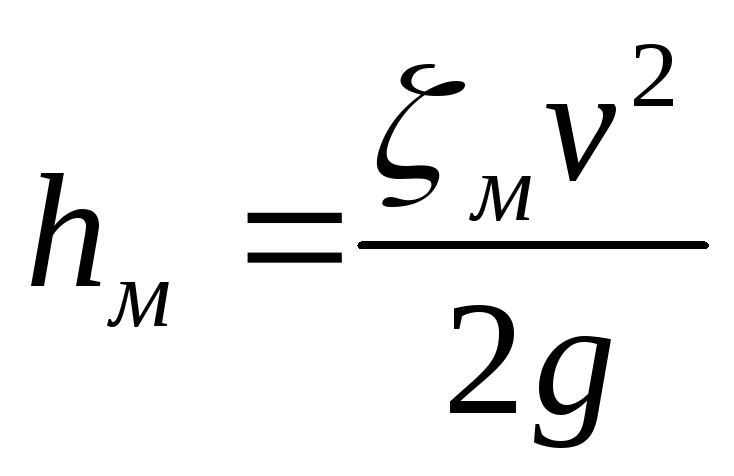 ,
,
или в единицах давления
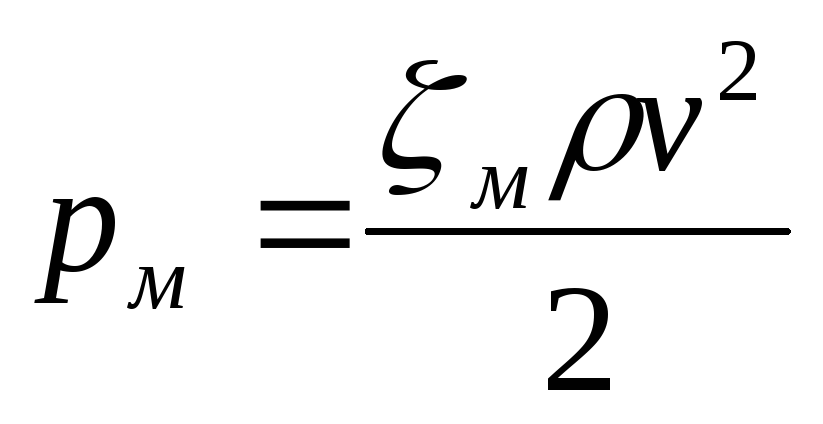 ,
,
где v — средняя по сечению скорость в трубе, в которой установлено данное местное сопротивление.
Если же диаметр трубы и, следовательно, скорость в ней изменяются по длине, то за расчетную скорость удобнее принимать бόльшую из скоростей, т.е. ту, которая соответствует меньшему диаметру трубы.
Каждое местное сопротивление характеризуется своим значением коэффициента сопротивления ζ, которое во многих случаях приближенно можно считать постоянным для данной формы местного сопротивления.
Потери на трение по длине, — это потери энергии, которые в чистом виде возникают в прямых трубах постоянного сечения, т.е. при равномерном течении, и возрастают пропорционально длине трубы. Рассматриваемые потери обусловлены внутренним в жидкости, а потому имеют место не только в шероховатых, но и гладких трубах.
Потери напора на трение можно выразить по общей формуле для гидравлических потерь, т.е.
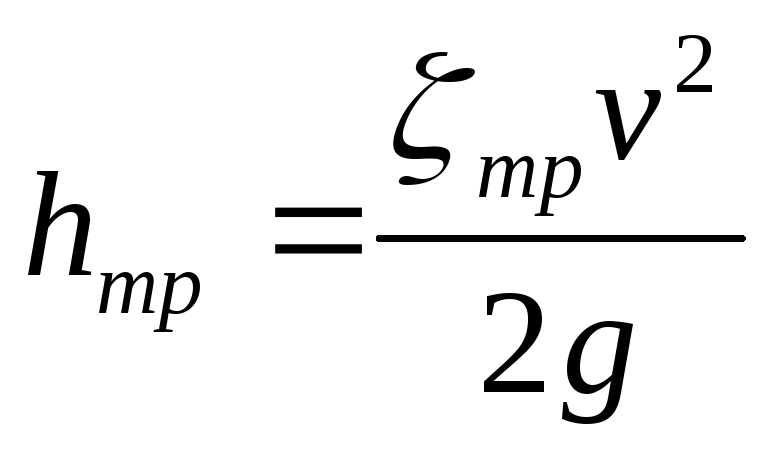 ,
,
однако удобнее коэффициент ζ связать с относительной длинной трубы l/d.
Возьмем участок круглой трубы длиной, равной ее диаметру, и обозначим его коэффициент потерь через λ. Тогда для всей трубы длинной l и диаметром d. коэффициент потерь будет в l/d раз больше:
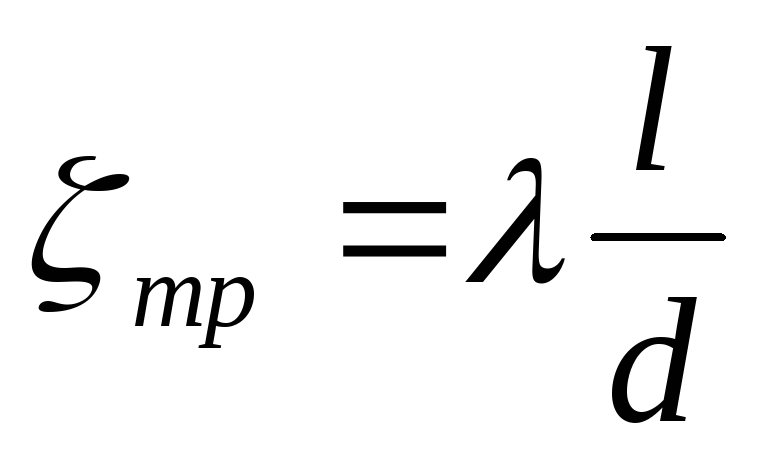 .
.
Тогда потери напора на трение определяются по формуле Вейсбаха-Дарси:
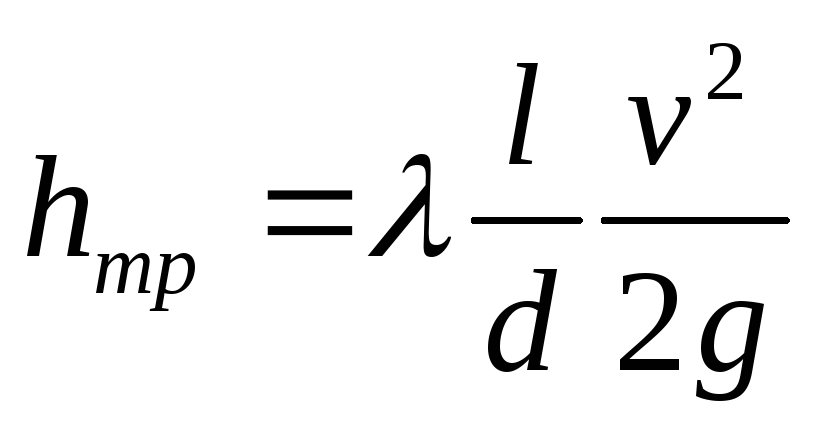 ,
,
или в единицах давления
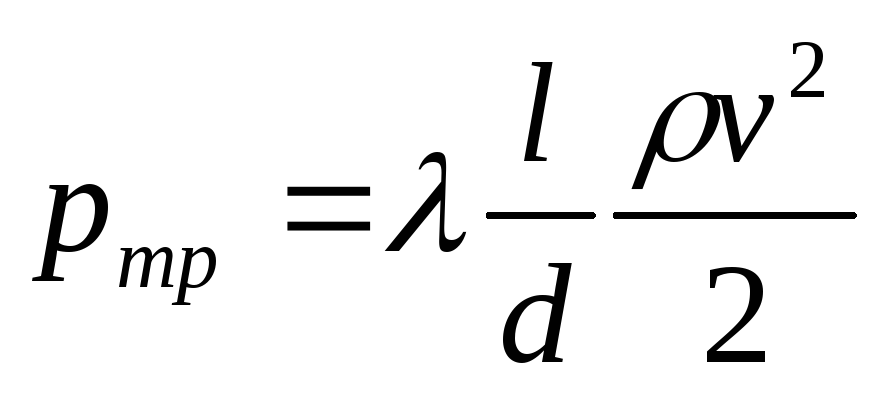 .
.
Безразмерный коэффициент λ называют коэффициентом потерь на трение по длине, или коэффициентом Дарси. Его можно рассматривать как коэффициент пропорциональности между потерей напора на трение, и произведением относительной длины трубы на скоростной напор.
Н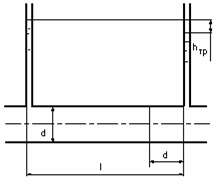 етрудно
выяснить физический смысл коэффициентаλ,
если рассмотреть условие равномерного
движения в трубе цилиндрического объема
длиной l и диаметром d,
т.е. равенство нулю суммы сил, действующих
на объем: сил давления и сил трения. Это
равенство имеет вид
етрудно
выяснить физический смысл коэффициентаλ,
если рассмотреть условие равномерного
движения в трубе цилиндрического объема
длиной l и диаметром d,
т.е. равенство нулю суммы сил, действующих
на объем: сил давления и сил трения. Это
равенство имеет вид
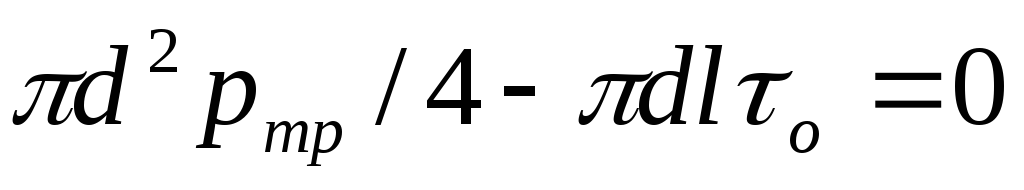 ,
,
где  —
напряжение трения на стенке трубы.
—
напряжение трения на стенке трубы.
Если
учесть 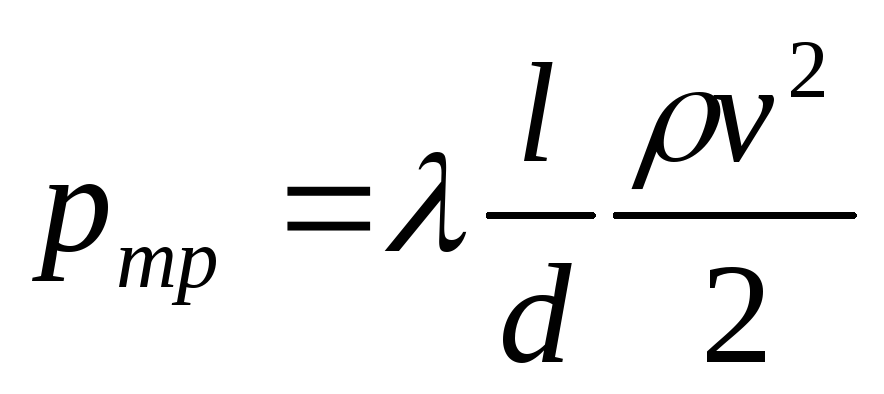 ,
томожно
получить
,
томожно
получить
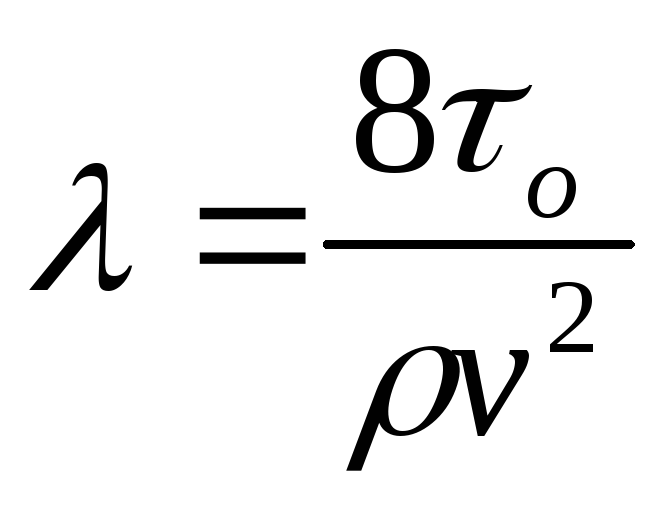 ,
,
т.е. коэффициент λ есть величина, пропорциональная отношению напряжения трения на стенке трубы к динамическому давлению, определенному по средней скорости.
Ввиду постоянства объемного расхода несжимаемой жидкости вдоль трубы постоянного сечения скорость и удельная кинетическая энергия также остаются постоянными, несмотря на наличие гидравлических сопротивлений и потерь напора. Потери напора в этом случае определяются разностью показаний двух пьезометров.
Лекция №10
studfile.net
6. РЕЖИМЫ ДВИЖЕНИЯ ЖИДКОСТИ
течение жидкости или газа, при котором жидкость (газ) перемещается как бы слоями, параллельными направлению течения. Наблюдаются или у очень вязких жидкостей: нефти, мазута, смазочных масел и в порах грунта при движении подземных вод, или при течениях, происходящих с достаточно малыми скоростями, а также при медленном обтекании жидкостью тел малых размеров. Ламинарное движение имеет место в узких (капиллярных) трубках, в слое смазки в подшипниках, в тонком пограничном слое, который образуется вблизи поверхности тел при обтекании их жидкостью или газом, и др. С увеличением скорости движения жидкости ламинарное движение может в некоторый момент перейти в неупорядоченное турбулентное, при этом резко изменяется сила сопротивления движению.
Турбулентное движение (от лат. turbulentus – бурный, беспорядочный), форма течения жидкости или газа, при которой их элементы совершают неупорядоченные, неустановившиеся движения по сложным траекториям, что приводит к интенсивному перемешиванию между слоями движущихся жидкости или газа. Турбулентный режим движения жидкостей встречается при движении маловязких жидкостей (вода, бензин, спирт) в трубах, каналах, реках. Наиболее детально изучены турбулентные движения в трубах, каналах, пограничных слоях около обтекаемых жидкостью или газом твёрдых тел, а также так называемые свободные турбулентные движения – струи, следы за движущимися относительно жидкости или газа твёрдыми телами и зоны перемешивания между потоками разной скорости, не разделённые какими-либо твёрдыми стенками. Турбулентные движения отличаются от ламинарных как своей сложной внутренней структурой, так и распределением осреднённой скорости по сечению потока и интегральными характеристиками – зависимостью средней по сечению или максимальной скорости, расхода, а также коэффициента сопротивления от числа Re.
Характер режима движения жидкости зависит от соотношения действующих в них сил. Если при движении жидкости преобладают силы вязкости, то режим ламинарный, если преобладают силы инерции, то наблюдается турбулентный режим движения потока. На это обстоятельство указывал в 1880 г. великий русский учёный Д. И. Менделеев и работе «О сопротивлении жидкости и воздухоплавании» которое было полностью изучено в 1883 г. английским физиком Рейнольдсом.
Рейнольдсом были произведены опыты, в которых рассматривался механизм различных видов движения жидкости (рис. 6.1). При разных условиях движения ему удалось установить зависимость между
studfile.net
13. Какие режимы движения жидкости или газа Вы знаете? Дайте их характеристику. С помощью какого критерия можно определить режим движения?
Различают два различных режима движения жидкости или газа: ламинарный и турбулентный.
При ламинарном режиме жидкость движется без пульсаций, параллельно стенкам канала (рис. а). При ламинарном движении скорость в поперечном сечении трубы изменяется по закону параболы
При турбулентном режиме жидкость или газ движутся хаотично со значительными пульсациями давления (рис. b). При турбулентном движении скорость в поперечном сечении трубы изменяется по закону трапеции.
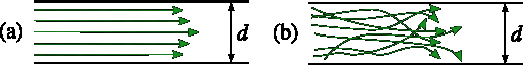
Определить режим движения можно по критерию Рейнольдса Re.
14. Запишите общий вид критериального уравнения для свободного движения теплоносителя.
Общий вид критериального уравнения при свободном стационарном движении жидкости имеет вид
Nu = f ( Gr, Pr)
Здесь Gr — критерий Грасгофа, характеризующий влияние на теплоотдачу подъемных сил и сил вязкости; Pr — критерий Прандтля, характеризующий теплофизические свойства вещества.
Если движение теплоносителя нестационарное, то критериальное уравнение имеет вид:
Nu = f ( Gr, Pr, Fo)
Здесь Fo — критерий Фурье, характеризующий нестационарный режим теплоотдачи.
15. Запишите общий вид критериального уравнения для вынужденного движения теплоносителя.
Для стационарного вынужденного движения теплоносителя критериальное уравнение имеет вид:
Nu = f ( Re, Pr)
Здесь Re — критерий Рейнольдса, характеризует режим движения теплоносителя, Pr — критерий Прандтля, характеризующий теплофизические свойства вещества.
Если движение теплоносителя нестационарное, то критериальное уравнение имеет вид:
Nu = f ( Re, Pr, Fo)
Здесь Fo — критерий Фурье, характеризующий нестационарный режим теплоотдачи.
16. Что такое «теплообмен излучением»? Каков его механизм.
Теплообмен излучения – процесс передачи тепла с помощью тепловых электромагнитных волн.
Лучистая энергия возникает в результате сложных молекулярных и атомных возмущений за счет тепловой энергии. При нагревании тела часть тепловой энергии всегда превращается в лучистую.
Носителем лучистой энергии являются электромагнитные волны, исходящие из излучаемого тела и распространяющиеся со скоростью света. Эти волны называются тепловыми, а процесс их распространения — тепловым излучением или лучеиспусканием.
Лучеиспускание присуще всем телам, и каждое из них излучает энергию непрерывно.
17. Запишите уравнение баланса лучистого теплообмена.
При попадании на другие тела энергия теплового излучения частично поглощается, частично отражается и частично проходит сквозь тело. Поглощенная телом энергия снова превращается в тепловую. Отраженная и прошедшая сквозь тело энергия попадает на другие тела и ими поглощается.
Уравнение баланса лучистого теплообмена имеет вид:
А + R + D = 1
Здесь величина А характеризует поглотительную способность тела; величина R — отражательную способность и величина D — пропускательную способность того же тела.
studfile.net
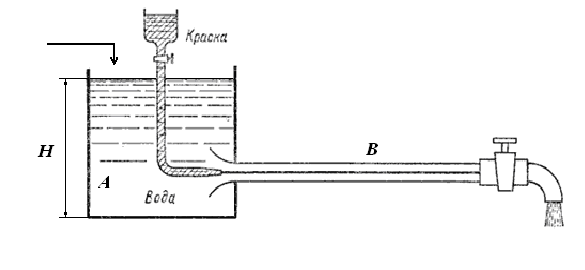
4.5. Режимы движения жидкости
Различные режимы течения жидкости можно проследить, вводя в поток подкрашенную струйку жидкости.
Впервые режимы течения жидкости изучались Рейнольдсом в 1883 г (рисунок 18).
| а б | |
|
| |
а | б | |
а –ламинарный, б-турбулентный режим движения Рисунок 18 – Опыт Рейнольдса | ||
К сосуду А, в котором поддерживается постоянный уровень воды Н, присоединена горизонтальная стеклянная труба В. В эту трубу по ее оси через капиллярную трубку вводится тонкая струйка окрашенной воды. При небольшой скорости воды в трубе окрашенная струйка вытягивается в горизонтальную нить, которая, не размываясь, достигает конца трубы (рисунок 18 а), это свидетельствует о том, что пути частиц прямолинейны и параллельны друг другу.
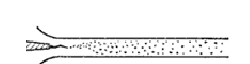
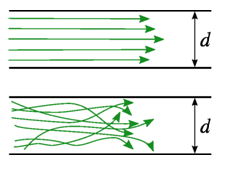
Такое движение, при котором все частицы жидкости движутся по параллельным траекториям, называют струйчатым или ламинарным.
Если скорость воды в трубе увеличивать сверх определенного предела, то окрашенная струйка сначала приобретает волнообразное движение, а затем начинает размываться, смешиваясь с основной массой воды. Это объясняется тем, что отдельные частицы жидкости движутся уже не параллельно друг другу и оси трубы, а перемешиваются в поперечном направлении (рисунок 19 б).
Такое неупорядочное движение, при котором отдельные частицы жидкости движутся по запутанным, хаотическим траекториям, в то время как вся масса жидкости в целом перемещается в одном направлении, называют турбулентным.
| а б |
Рисунок 19 – Схематичное изображение ламинарного (a) и турбулентного (б) течения в плоском слое | |
В турбулентном потоке происходят пульсации скоростей, под действием которых частицы жидкости, движущиеся в главном (осевом) направлении, получают также поперечные перемещения, приводящие к интенсивному перемешиванию потока по сечению и требующие соответственно большей затраты энергии на движение жидкости, чем при ламинарном потоке.
Опыт показывает, что переход от ламинарного течения к турбулентному происходит тем легче, чем больше плотность жидкости ρ, скорость движения жидкости v и диаметр трубы d, и чем меньше вязкость жидкости μ. Рейнольдс установил, что указанные величины можно объединить в безразмерный комплекс, значение которого позволяет судить о режиме движения жидкости. Этот комплекс носит название критерия (числа) Рейнольдса:
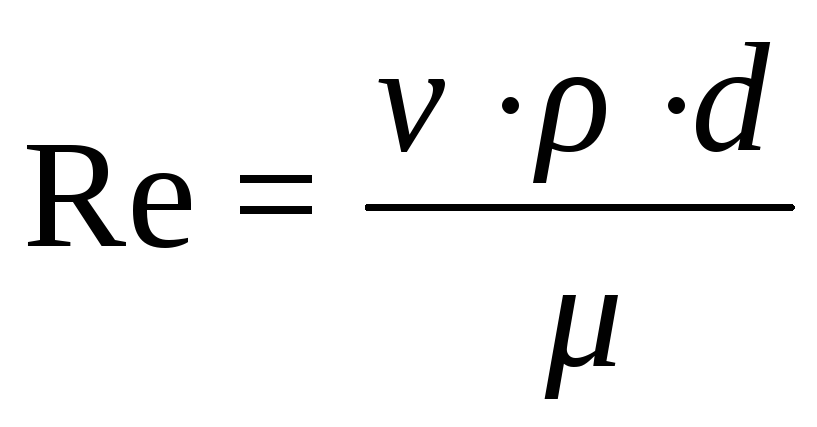 ,
,
Физический смысл критерия Рейнольдса заключается в том, что он является мерой соотношения между силами инерции и вязкости в движущемся потоке.
С учетом того, что
кинематический коэффициент вязкости 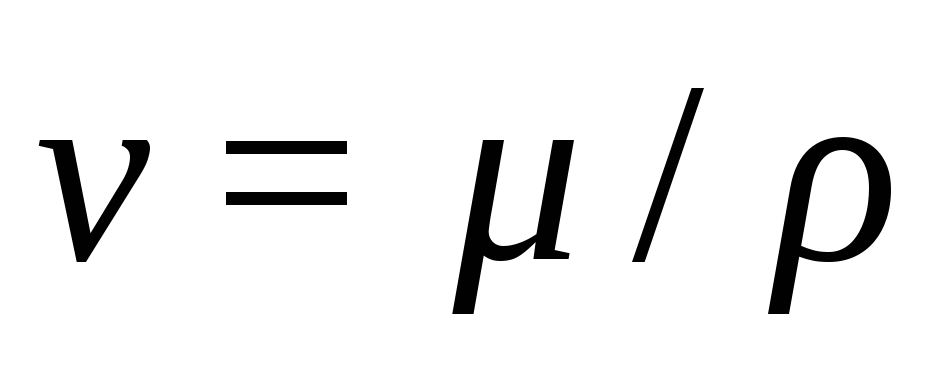 ,
то критерий Рейнольдса можно записать:
,
то критерий Рейнольдса можно записать:
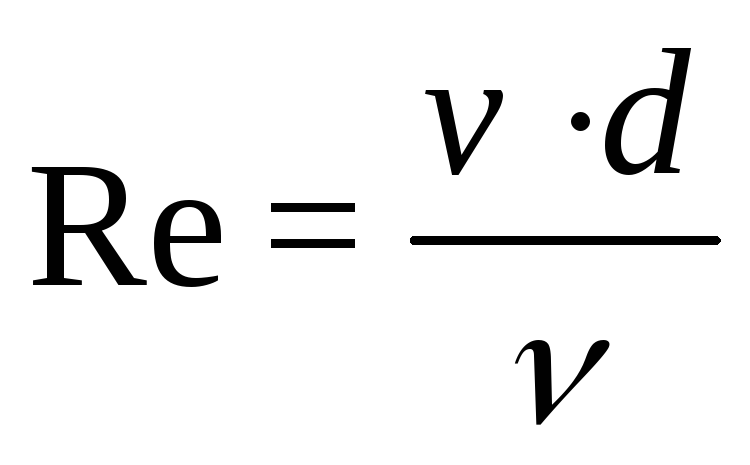 ,
,
Переход от
ламинарного режима движения к турбулентному
характеризуется критическим значением
критерия Рейнольдса Reкр1.
При движении жидкости по прямым гладким
трубам для изотермического потока
критическое значение критерия Рейнольдса
составляет 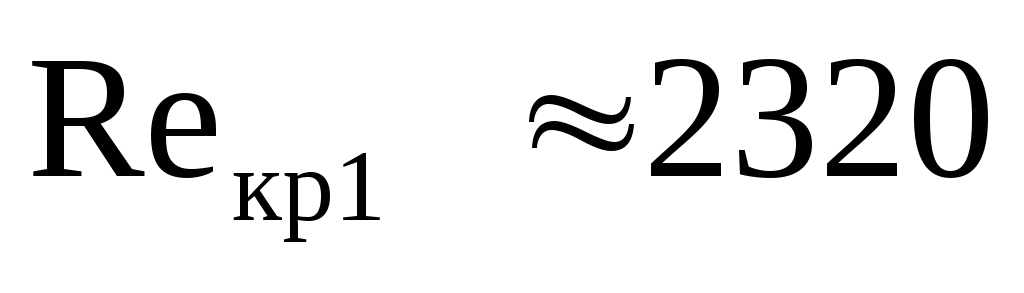 .
При
.
При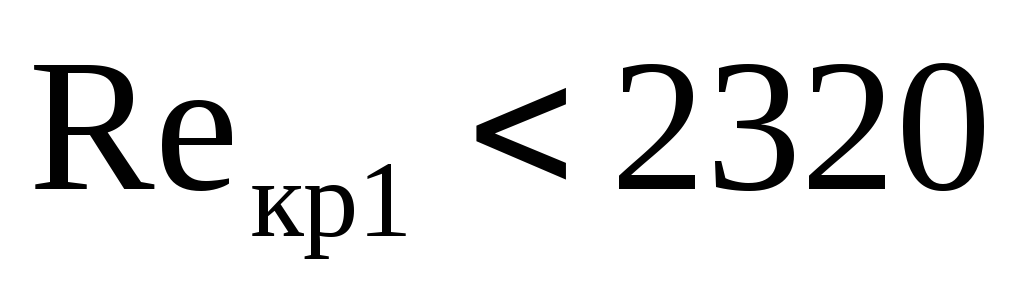 течение являетсяламинарным и данную область значений
течение являетсяламинарным и данную область значений  называют областьюустойчивого
ламинарного режима течения.
При значении критерия Рейнольдса
называют областьюустойчивого
ламинарного режима течения.
При значении критерия Рейнольдса 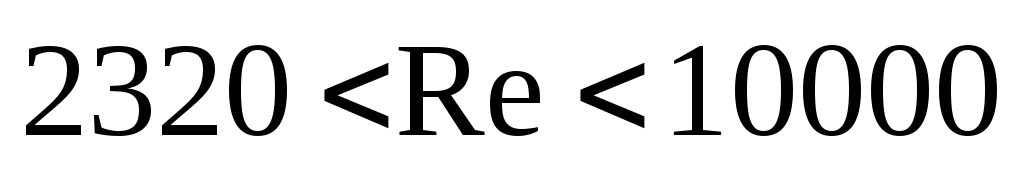 режим течения еще неустойчиво турбулентный
и эту область называютпереходной. Лишь при
режим течения еще неустойчиво турбулентный
и эту область называютпереходной. Лишь при 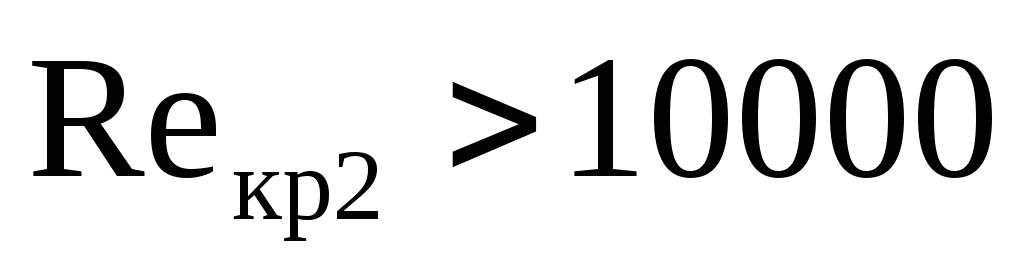 турбулентное
движение становиться устойчивым
(развитым).
турбулентное
движение становиться устойчивым
(развитым).
Критические значения числа Рейнольдса зависят от вида течения. Так наличие различных возмущений, обусловленных шероховатостью стенок трубы, изменением скорости движения жидкости или ее направления существенно влияет на критические значения числа Рейнольдса.
Скорость, при которой для данной жидкости и определенного диаметра трубопровода происходит смена режимов движения, называется критической.
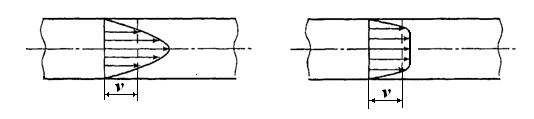
При ламинарном режиме движения скорость имеет максимальное значение на оси трубы. У стенок трубы скорость равна нулю, т.к. частицы жидкости покрывают внутреннюю поверхность трубопровода тонким неподвижным слоем. От стенок трубы к ее оси скорости нарастают плавно согласно уравнению:
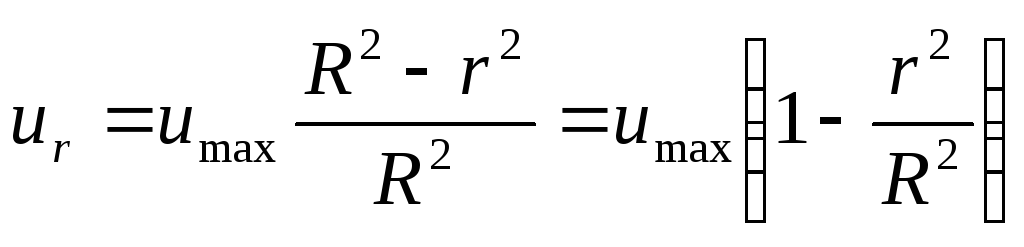 ,
,
где umax – максимальная скорость движения жидкости, м/с;
R – радиус трубы, м;
r — радиус движущегося слоя жидкости, м
Последнее уравнение представляет собой закон Стокса, выражающий параболитическое распределение скоростей в сечении трубопровода при ламинарном движении (рис.19 а).
При ламинарном потоке в трубе средняя скорость жидкости равна половине скорости по оси трубы:
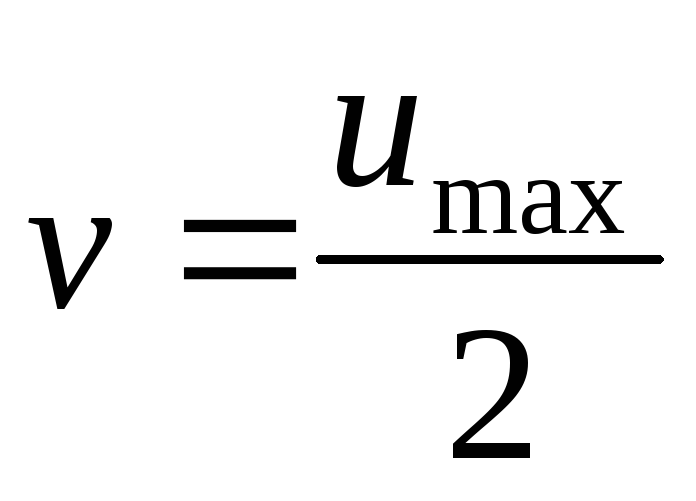 .
.
При турбулентном режиме движения жидкости в трубах эпюра распределения скоростей имеет вид, показанный на рисунке 20 б.
|
а б |
Рисунок 20 — Сопоставление формы профиля скорости ламинарного (а) и турбулентного течения (б).
Средняя скорость v при турбулентном движении не равна половине максимальной (как для ламинарного движения), а значительно больше, причем v/umax= f(Re). Например, при Re = 104 скорость v= 0,8 umах, а при Re = 108 величина v = 0,9 umах.
На практике чаще всего встречается турбулентный режим движения (движение воды в трубах, каналах, реках и т.п.). Ламинарный режим движения встречается при движении по трубам жидкостей с большой вязкостью (нефти, нефтепродуктов и т.д.), а также при движении воды в тонких капиллярных трубках и порах грунта [2-4,9].
studfile.net
Изучение режимов движения жидкости
Министерство образования и науки Российской Федерации
Национальный исследовательский ядерный университет «МИФИ»
Балаковский инженерно-технологический
Методические указания к выполнению лабораторной работы
по дисциплинам: «Гидравлика», «Механика жидкости и газа», «Водоснабжение и водоотведение с основами гидравлики», «Гидрогазодинамика», «Гидравлика и гидропневмопривод»
для студентов направлений: «Теплоэнергетика и теплотехника», «Строительство», «Конструкторско-технологическое обеспечение машиностроительных производств», «Строительство уникальных зданий и сооружений» », «Наземные транспортно-технологические средства»
профиль «Подъемно-транспортные, строительные, дорожные средства и оборудование»
очной, заочной и заочно-сокращенной форм обучения
\
Балаково 2015
ЦЕЛЬ РАБОТЫ: изучить ламинарный, критический и турбулентный режимы течения жидкости.
Основные понятия
Движение жидкостей и газов может происходить в двух качественно различных режимах — ламинарном и турбулентном.
Ламинарным называется слоистое движение без перемешивания частиц жидкости и без пульсации скорости и давления. При ламинарном течении жидкости в прямой трубе постоянного сечения все линии тока направлены параллельно оси трубы.
Турбулентным (или хаотичным) называется движение, сопровождающееся интенсивным перемешиванием жидкости с пульсациями скорости и давления. Наряду с основным продольным перемещением жидкости наблюдаются поперечные перемещения и вращательные движения отдельных объемов жидкости.
Переход от одного режима к другому происходит через критический режим, где движение жидкости уже не ламинарное, но еще не турбулентное.
Для оценки режима движения жидкости 0.Рейнольдсом был предложен безразмерный критерий, учитывающий физические свойства жидкости (плотность ρ, вязкость μ, ), кинематические характеристики потока (среднюю скорость потока V) и геометрические параметры (диаметр трубы d или гидравлический радиус R ):
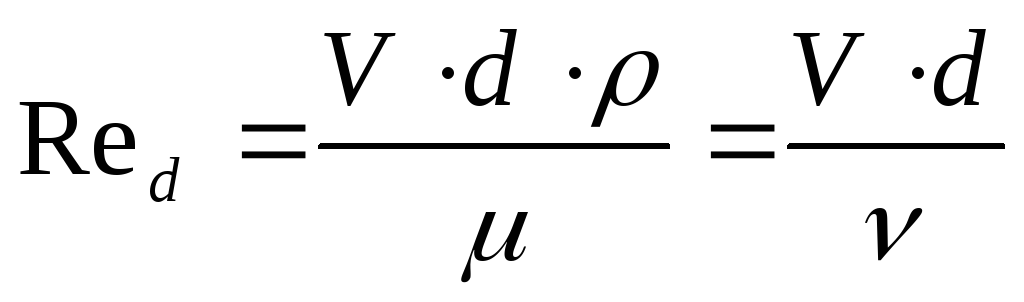 ;
(1)
;
(1)
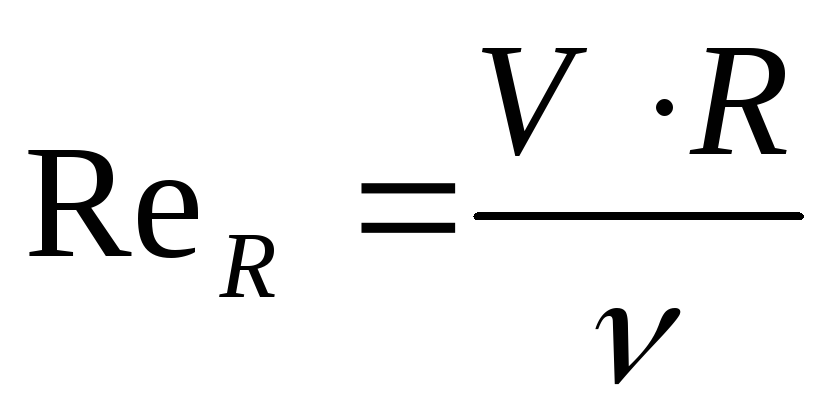 ;
(2)
;
(2)
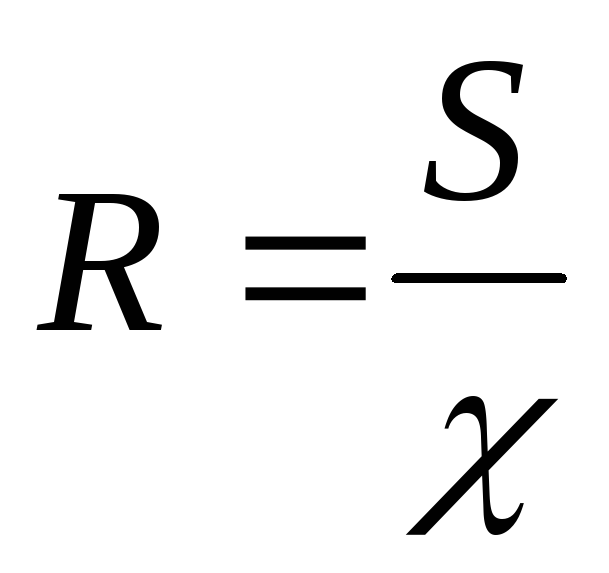 ,
(3)
,
(3)
где Red — число Рейнольдса для круглых труб, работающих в напорном режиме;
ReR — число Рейнольдса для живого сечения некруглой формы;
μ — динамический коэффициент вязкости жидкости;
— кинематический коэффициент вязкости жидкости;
S — площадь живого сечения ;
χ — смоченный периметр.
Число Рейнольдса является критерием частичного динамического подобия потоков, когда преобладающими являются силы инерции и трения, и представляет собой отношение сил инерции к силам трения.
Режим движения жидкости существенным образом зависит от соотношения действующих сил. Если при движении жидкости преобладают силы трения, то режим движения ламинарный. С возрастанием скорости движения жидкости ламинарное движение сохраняется до определенного значения средней скорости, которая называется критической (Vкр). Дальнейшее увеличение скорости сверх критической приводит к нарушению слоистости и образованию вихрей, движение частиц жидкости приобретает хаотичный характер. В этом случае начинают преобладать силы инерции и режим движения становится турбулентным.
Критической скорости движения жидкости соответствует критическое число Рейнольдса:
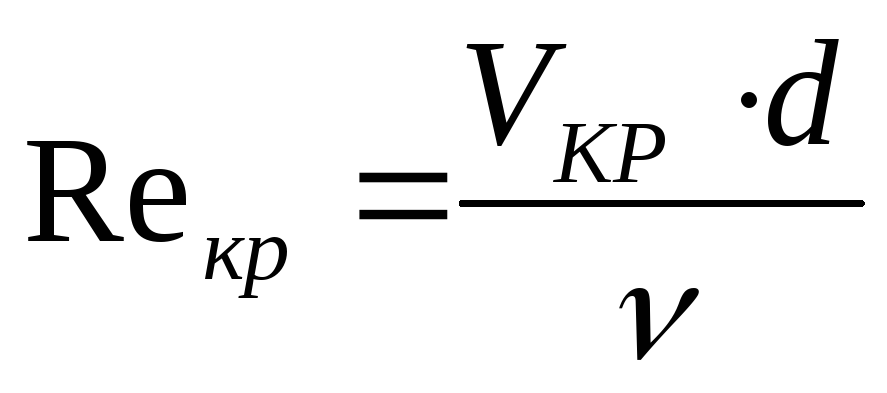 .
(4)
.
(4)
Для круглых напорных труб критическое число Рейнольдса Rекр = 2300, а для русел круглого сечения Rекр=575.
Таким образом, число Рейнольдса позволяет установить режим движения жидкости:
при Re<Reкр — движение ламинарное,
при Re>Reкр — движение турбулентное.
МЕТОДИКА ЭКСПЕРИМЕНТА
С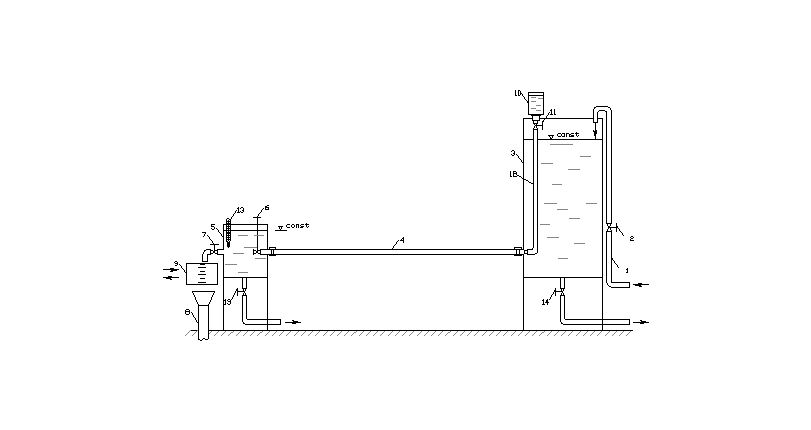 хема
лабораторной установки для исследования
режимов движения жидкости приведена
на рисунке 1.
хема
лабораторной установки для исследования
режимов движения жидкости приведена
на рисунке 1.
Рис. 1. Схема лабораторной установки
Подача воды в напорный бак 3 осуществляется на трубе 1 при помощи вентиля 2. Из напорного бака вода поступает в приемный бак 5 по стеклянной трубке 4. Регулирование расходов и, соответственно, скоростей движения воды осуществляется при помощи вентиля 6. Вентиль 7 служит для поддерживания уровня воды в приемном баке постоянным. Из приемного бака вода поступает в мерный бак 9. Краситель из бачка 10 по трубке 12 подается в стеклянную трубку 4. Подача красителя регулируется при помощи крана 11. Температура воды измеряется при помощи термометра 13. Вентили 14 и 13 служат для опорожнения баков.
Режимы движения жидкости устанавливают визуально, наблюдая за поведением красителя в стеклянной трубке 4. В качестве красителя используется окрашенная жидкость одинаковой с основной жидкостью плотности.
При ламинарном режиме краситель течет, не перемешиваясь, с основным потоком и напоминает окрашенную нитку, натянутую внутри стеклянной трубки. С увеличением скорости потока жидкости, в определенный момент, струйка красителя начинает изгибаться. При дальнейшем увеличении скорости потока начинают образовываться отдельные вихри, а затем краситель интенсивно перемешивается с потоком.
Ламинарный режим течения жидкости исследуется до начала деформации струйки красителя, критический режим — в момент начала деформации струйки красителя, турбулентный режим — когда струйка красителя интенсивно перемешивается с потоком жидкости.
При исследованиях каждого режима течения движение необходимо поддерживать установившимся. Для этого уровень жидкости в баке 3 поддерживают постоянным.
При выполнении работы измеряются следующие параметры потока:
— температура жидкости, t °С,
— расход жидкости, Q .
Температура жидкости измеряется в нижнем баке при помощи термометра с погрешностью ± 0,5 °С.
Расход жидкости Q определяется объемным способом при помощи мерного сосуда и секундомера:
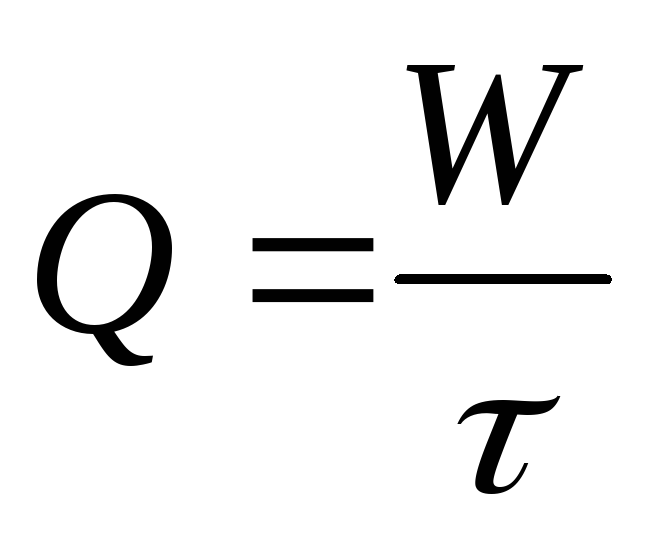 ,
(5)
,
(5)
где W — объем мерного сосуда, см3 ;
τ — время наполнения мерного сосуда, с.
ТРЕБОВАНИЯ БЕЗОПАСНОСТИ ТРУДА
1. Перед проведением опытов необходимо повторить инструкцию по правилам безопасности работы в лаборатории.
2. Изучить описание установки, подготовить необходимые приборы, выяснить непонятные вопросы у преподавателя. Приступать к проведению опытов только с разрешения преподавателя.
3. При проведении опыта аккуратно обращаться со стеклянными и хрупкими приборами и оборудованием лабораторной установки.
4. При возникновении затруднений в выполнении опытов, а также поломки приборов и оборудования, необходимо прекратить опыты и обратиться к преподавателю.
5. В случае получения травмы необходимо немедленно прекратить опыты и обратиться к преподавателю за медицинской помощью.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Подготовка установки к проведению опытов.
1.1. Открывают вентиль 2 и заполняют напорный бак 3 водой, слоем около 1м. При этом вентиль 6 должен быть закрытым.
1.2. При закрытом кране 11 заполняют бачок 10 красителем.
1.3. Измеряют внутренний диаметр d стеклянной трубки 4.
2. Исследование ламинарного режима движения жидкости.
2.1. При закрытом вентиле 7 открыть вентиль 6 и заполнить бак 5, не допуская его переполнения.
2.2. Открыть кран 11 для подачи красителя. Одновременно, регулируя открытие вентилей 7 и 6, визуально добиваются того, чтобы струйка красящей жидкости в стеклянной трубке не перемешивалась с водой и приняла вид прямой горизонтальной линии.
2.3. При проведении опыта уровень воды в напорном баке 3 поддерживают постоянным при помощи вентиля 2, а в баке 5 при помощи вентиля 7.
2.4. После стабилизации режима движения воды измеряют температуру и расход воды. Расход воды определяют объемным способом. Для этого определяют время наполнения мерного сосуда 9 при помощи секундомера. Результаты измерений записываются в таблицу.
3. Исследование критического режима.
3.1. Открытием вентилей 5 и 7 визуально добиваются начала перемешивания струйки красителя в стеклянной трубке 4.
3.2. После установления стабильного режима производят измерения по п.2.4. При этом, уровни воды в баках 3 и 5 поддерживаются постоянными. Результаты опыта записывают в таблицу.
4. Исследование турбулентного режима движения жидкости.
4.1. Открытием вентилей 5 и 7 визуально добиваются интенсивного перемешивания струйки красителя в стеклянной трубке 4.
4.2. После установления стабильного режима производят измерения по п.2.4. Результаты измерений записывают в таблицу.
Таблица 1
Результаты опытов
№№ | Наименование измерений и вычислений | единица измерения | №№ опытов | |||||
1 | 2 | 3 | ||||||
1 | 2 | 3 | 4 | 5 | 6 | |||
1 | Размеры трубы | |||||||
1 | Диаметр стеклянной трубки | см | ||||||
2 | Площадь поперечного сечения трубки, S | см2 | ||||||
Определение расхода и средней скорости воды в трубке | ||||||||
3 | Объем мерного бака, W | см3 | ||||||
4 | Время заполнения мерного бака, τ | с | ||||||
5 | Расход воды, Q | см3/с | ||||||
6 | Сpeдняя скорость, V | см/с | ||||||
Определение числа Рейнольдса и режима движения | ||||||||
7 | Температура воды, t | °С | ||||||
8 | Кинематический коэффициент вязкости воды, ν | см2/с | ||||||
9 | Число Рейнольдса , Re | |||||||
10 | Режим движения воды | |||||||
Определение погрешности эксперимента | ||||||||
11 | Относительная
погрешность определения площади, | |||||||
12 | Относительная
погрешность определения расхода, | |||||||
13 | Относительная
погрешность определения скорости, | |||||||
14 | Относительная
погрешность определения числа
Рейнольдса, | |||||||
ОБРАБОТКА РЕЗУЛЬТАТОВ ЭKCПЕРЕМЕНТА
В таблицу 1 записываются результаты измерений. Затем выполняются расчеты в следующей последовательности:
1. Вычисляется площадь поперечного сечения стеклянной трубы S:
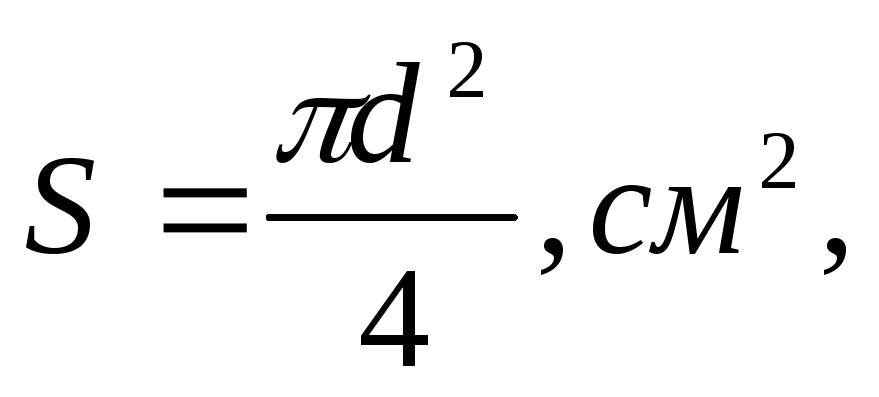 (6)
(6)
где d — внутренний диаметр трубы, см.
2. Вычисляется расход жидкости Q , см3/с по (5).
3. Вычисляется средняя скорость потока жидкости V:
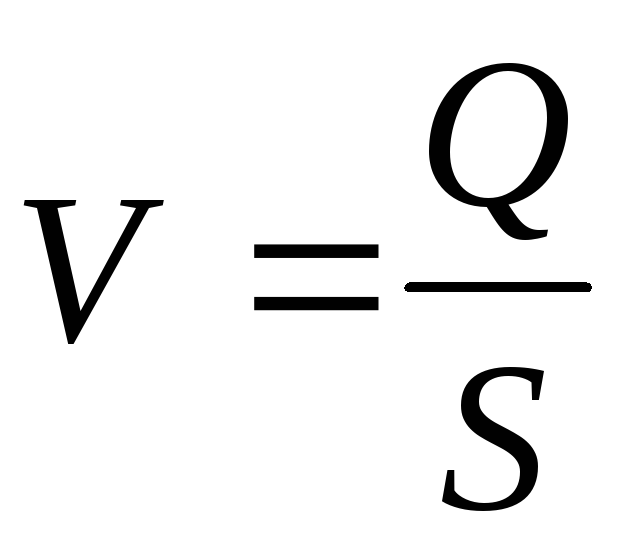 ,
,  .
(7)
.
(7)
4. Из приложения определяют кинематический коэффициент вязкости воды см2 /с в соответствии с измеренной температурой °С.
5. Вычисляют число Рейнольдса Re, соответствующее каждому опыту:
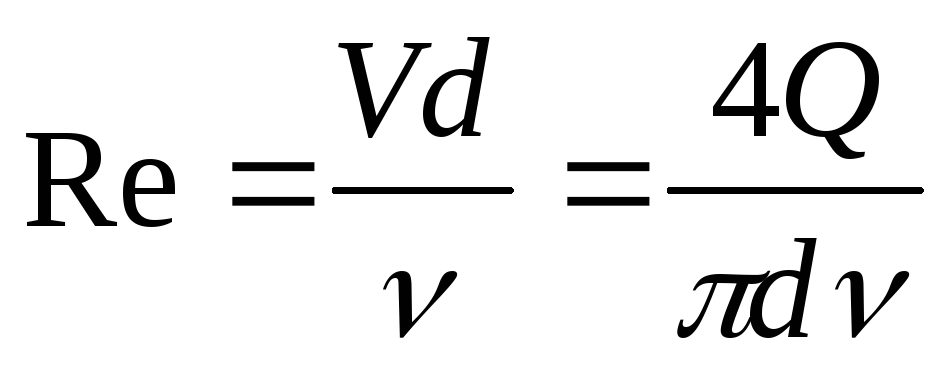 (8)
(8)
6. Сравнивают число Рейнольдса по опыту Re опкр, соответствующее критическому режиму с Re кр =2300, и вычисляют погрешность задания режима движения вызванную конструктивным исполнением экспериментальной установки:
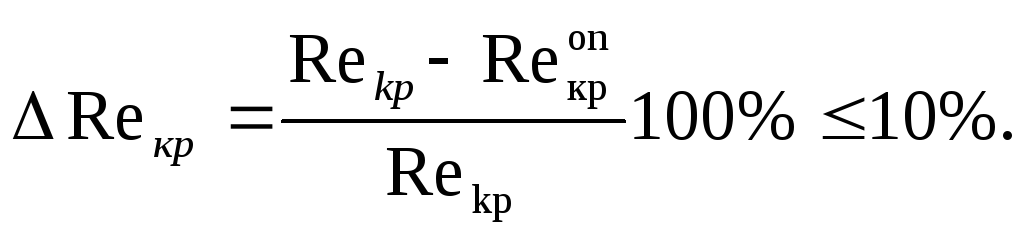
7. Проверяют выполнение условий:
Re<Reкр — режим ламинарный,
Re>Reкр — режим турбулентный.
В случае невыполнения этих условий или большой погрешности определения критического числа Рейнольдса определить причину.
Определение погрешности эксперимента
Случайными погрешностями пренебрегают и рассматривают только систематические погрешности. Погрешность определения площади, расхода, скорости и числа Рейнольдса определяется как погрешность косвенных измерений.
Согласно выражениям (5) — (8), относительная погрешность определения площади, расхода, скорости и числа Рейнольдса составит:
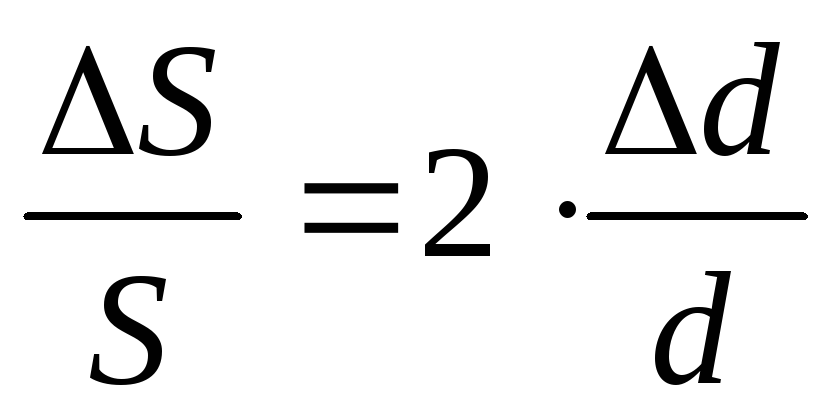 ,
(9)
,
(9)
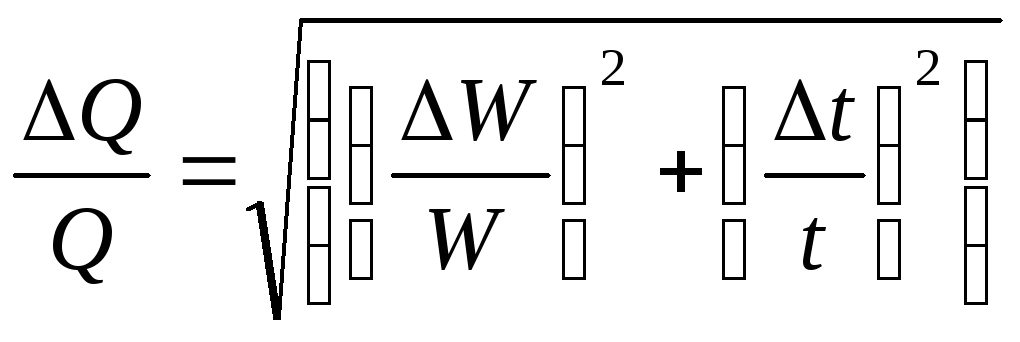 ,
(10)
,
(10)
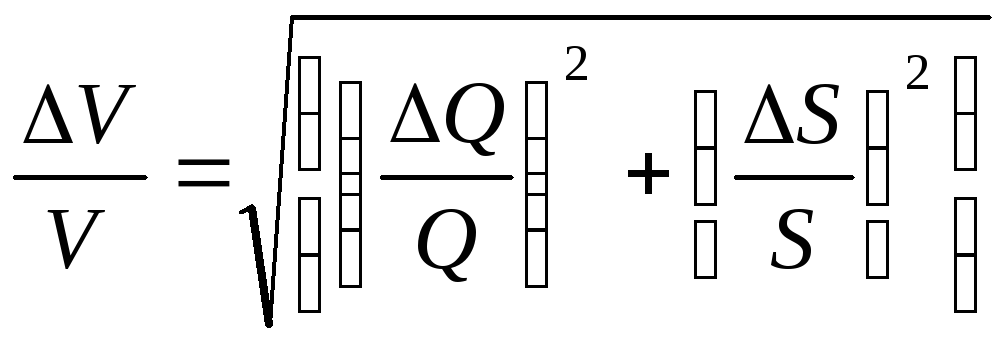 ,
(11)
,
(11)
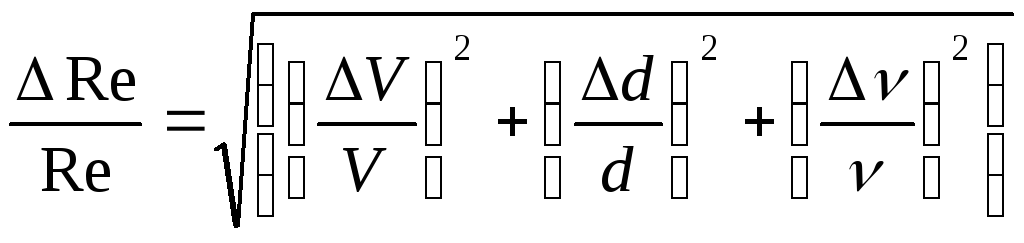 ,
(12)
,
(12)
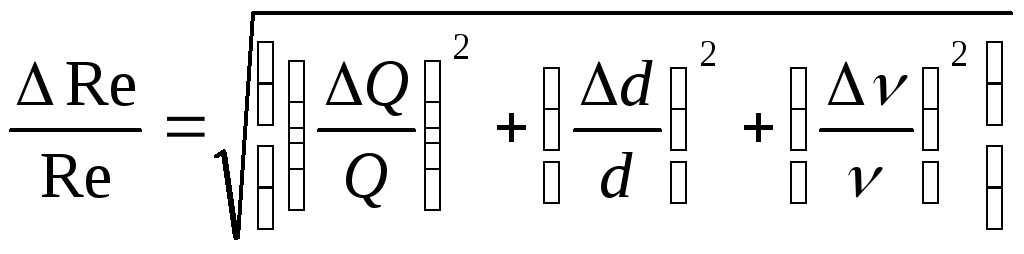 ,
(13)
,
(13)
Через  обозначены абсолютные ошибки измерения
отдельных величин, входящих в выражения
(9) — (13).
обозначены абсолютные ошибки измерения
отдельных величин, входящих в выражения
(9) — (13).
В данной работе экспериментально измеряется время наполнения мерной емкости, внутренний диаметр трубы и температура жидкости.
Объем мерного сосуда определяют с погрешностью DW = ± 10 см3, время его наполнения с погрешностью Dt = ± 0,2 с, Погрешность кинематического коэффициента вязкости воды n определить в соответствии с погрешностью измерения температуры. Температуру воды измеряют термометром с погрешностью ± 0,5 °С. Внутренний диаметр стеклянной трубки измеряется по дубликату при помощи штангенциркуля с погрешностью не более ± 0,1 мм.
Погрешности по формулам (9 — 13) рассчитываются для всех опытов. Далее делается анализ полученных результатов, намечаются пути увеличения точности опытов. По согласованию с преподавателем каждым студентом звена делается расчет одного из предложенных мероприятий по снижению погрешности. По результатам всех расчетов делается общий вывод о возможности увеличении точности опытов до заданной преподавателем величины.
studfile.net

 ;
;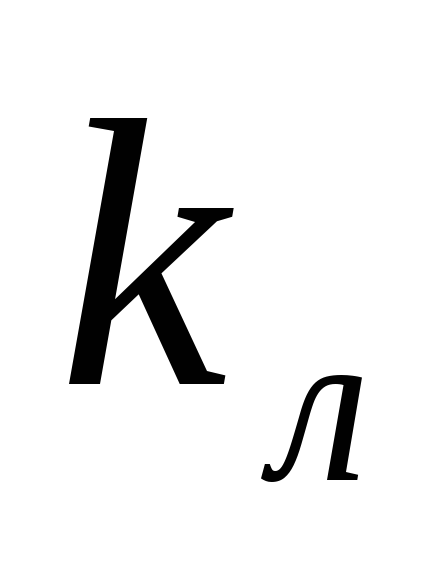

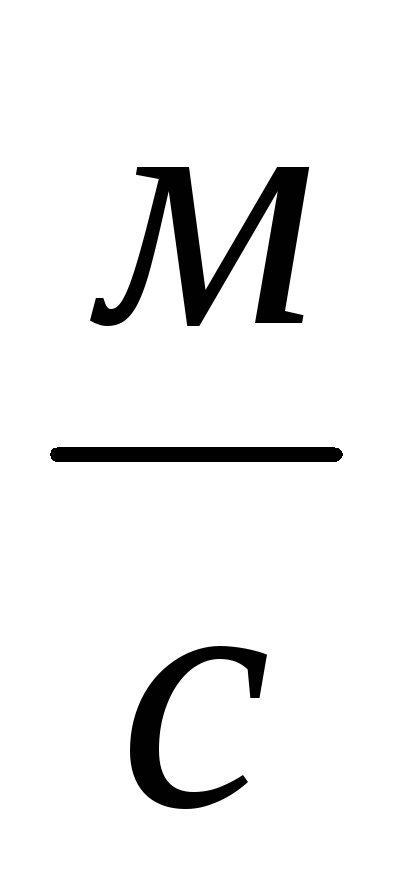 .
.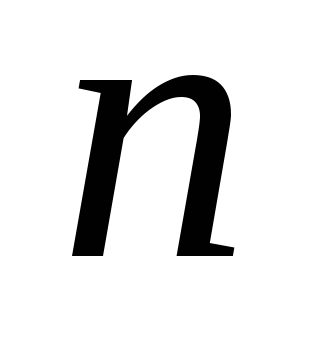



 ;
;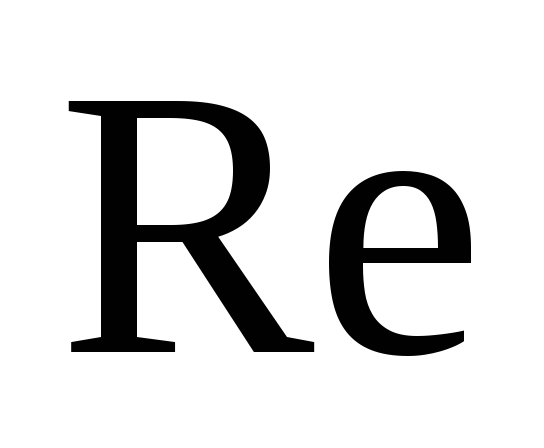

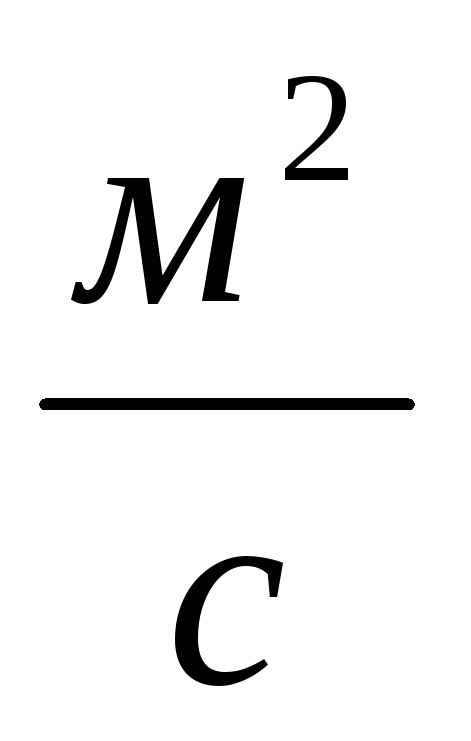 ;
;
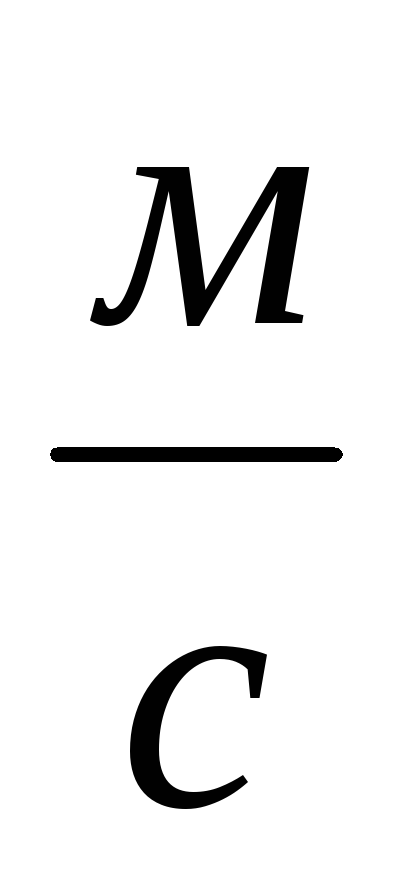
 1,0
1,0 0,01
0,01 0,03
0,03 1,5
1,5 0,1
0,1 0,15
0,15 1,0
1,0 1,5
1,5 0,8
0,8 0,1
0,1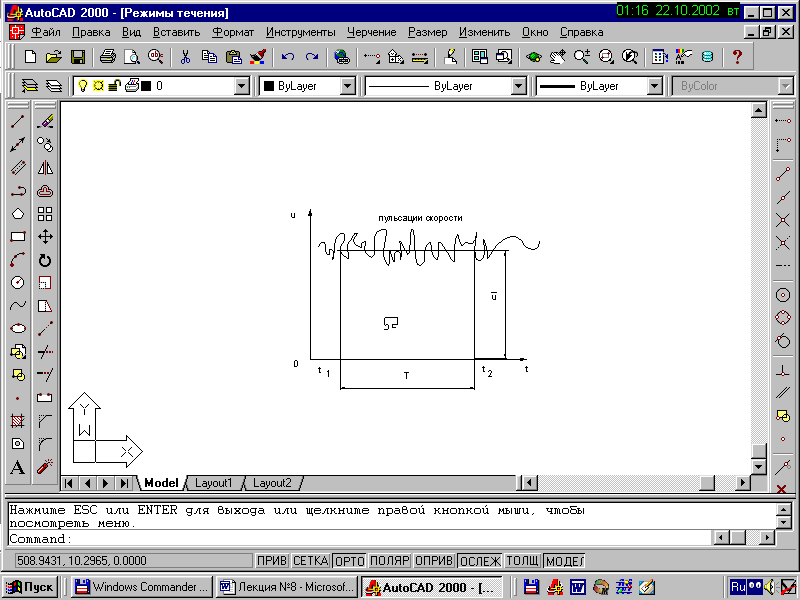
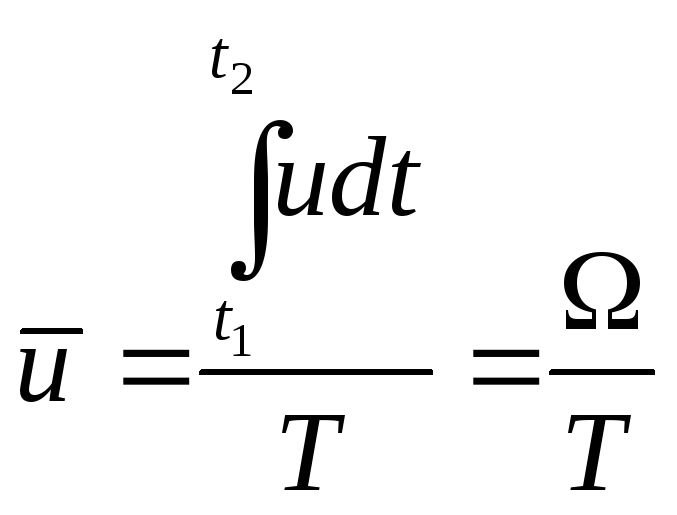 .
.