Расстояние от точки до плоскости онлайн
С помощю этого онлайн калькулятора можно найти расстояние от точки до заданной плоскости. Дается подробное решение с пояснениями. Для вычисления расстояния от точки до плоскости введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку «Решить».
Очистить все ячейки?
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Расстояние от точки до плоскости − теория, примеры и решения
Для нахождения расстояния от точки M0 до плоскости α, необходимо найти расстояние от точки M0 до проекции точки M0 на плоскость α:
Нахождение расстояния от точки до плоскости содержит следующие шаги:
- построение прямой L, проходящей через точку M0 и перпендикулярной плоскости α.

- нахождение точки M1 пересечения плоскости α с прямой L(Рис.1).
- вычисление расстояния между точками M0 и M1.
1. Общее уравнение плоскости имеет вид:
где n(A,B,C)− называется нормальным вектором плоскости.
Уравнение прямой, проходящей через точку M0(x0, y0, z0) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:
Для того, чтобы прямая (2) была ортогональна плоскости (1), направляющий вектор q(l, m, n) прямой (2) должен быть коллинеарным нормальному вектору n(A,B,C) плоскости (1)(Рис. 1). Следовательно, в качестве направляющего вектора прямой (2) можно взять нормальный вектор плоскости (1) .
Таким образом, уравнение прямой, проходящей через точку M0(x0, y0, z0) и ортогональной плоскости (1) имеет следующий вид:
Для нахождения точку пересечения прямой L с плоскостью α, проще всего рассматривать параметрическое уравнение прямой.
Выразим переменные x, y, z через рараметр t.
2. Найдем точку пересечения прямой (4) с плоскостью (1). Для этого нужно найти такой параметр t, при котором точка M(x, y, z) принадлежит плоскости (1). Поэтому подставим значения x,y,z из выражения (4) в (1) и решим относительно t.
Подставляя значение параметра t в выражения (4), находим проекцию M1(x1, y1, z1) точки M0 на плоскость (1).
3. Найдем, наконец, расстояние от точки M0 до плоскости (1). Очевидно, что расстояние от точки
Учитывая значение параметра t, имеем:
Пример 1. Найти расстояние от точки M0(2, -1, -9/31) до плоскости
Решение.
Нормальный вектор плоскости имеет вид:
т.е. A=5, B=1, C=2.
Координаты точки M0: x0=2, y0=−1, z0=−9/31.
Подставляя координаты точки M0 и нормального вектора плоскости в (5), получим:
Из выражений (4) находим:
Проекцией точки M0(2, -1, -9/31) на плоскость (7) является точка:
Вычислим расстояние между точками M0 и M1:
Упростим:
Ответ:
Расстояние от точки M0(2, -1, -9/31) до плоскости (7):
Расстояние от точки до плоскости
Поиск расстояния от точки до плоскости — частая задача, возникающая при решении различных задач аналитической геометрии, например, к этой задаче можно свести нахождение расстояния между двумя скрещивающимися прямыми или между прямой и параллельной ей плоскостью.
Рассмотрим плоскость $β$ и точку $M_0$ с координатами $(x_0;y_0; z_0)$, не принадлежащую плоскости $β$.
Определение 1
Кратчайшим расстоянием между точкой и плоскостью будет перпендикуляр, опущенный из точки $М_0$ на плоскость $β$.
Рисунок 1. Расстояние от точки, до плоскости. Автор24 — интернет-биржа студенческих работ
Помощь со студенческой работой на тему
Расстояние от точки до плоскости
Ниже рассмотрено как найти расстояние от точки до плоскости координатным методом.
Вывод формулы для координатного метода поиска расстояния от точки до плоскости в пространстве
Перпендикуляр из точки $M_0$, пересекающийся с плоскостью $β$ в точке $M_1$ с координатами $(x_1;y_1; z_1)$, лежит на прямой, направляющим вектором которой является нормальный вектор плоскости $β$. При этом длина единичного вектора $n$ равна единице. Соответственно этому, расстояние от $β$ до точки $M_0$ составит:
$ρ= |\vec{n} \cdot \vec{M_1M_0}|\left(1\right)$, где $\vec{M_1M_0}$ — нормальный вектор плоскости $β$, а $\vec{n}$ — единичный нормальный вектор рассматриваемой плоскости. 2}}\left(4\right)$
2}}\left(4\right)$
Равенство $(4)$ является формулой для нахождения расстояния от точки до плоскости в пространстве.
Общий алгоритм для нахождения расстояния от точки $M_0$ до плоскости
- Если уравнение плоскости задано не в общей форме, для начала необходимо привести его к общей.
- После этого необходимо выразить из общего уравнения плоскости нормальный вектор данной плоскости через точку $M_0$ и точку, принадлежащую заданной плоскости, для этого нужно воспользоваться равенством $(3)$.
- Следующий этап — поиск координат единичного нормального вектора плоскости по формуле $(2)$.
- Наконец, можно приступить к поиску расстояния от точки до плоскости, это осуществляется с помощью вычисления скалярного произведения векторов $\vec{n}$ и $\vec{M_1M_0}$.
Пример 1
Найдите расстояние от точки $M_0$, заданной координатами $(1;2;3)$ до плоскости $β$, заданной уравнением $5x+2y-z+3=0$
Воспользуемся формулой $(4)$:
$ρ=\frac{|5 \cdot 1 + 2 \cdot 2 -3 \cdot1+3|}{\sqrt{5^2 + 2^2 + (-1)^2}}=\frac{9}{\sqrt{30}}$.
Как инструменты близости вычисляют расстояние—ArcGIS Pro
Как определяется расстояние
Расстояние между любыми двумя объектами вычисляется как минимальный интервал между ними, т.е., там, где два объекта расположены ближе всего друг к другу. Эта логика действует во всех инструментах геообработки, которые вычисляют расстояние, включая такие инструменты, как Ближайший объект, Построить таблицу ближайших объектов и Пространственное соединение (с опцией ближайших совпадений).
Измерения расстояний имеют наибольшую точность, если входные данные используют систему координат равнопромежуточной проекции. Хотя вычисление расстояния может быть выполнено независимо от системы координат, результат может оказаться не точным или даже бессмысленным, если данные используют географическую систему координат или система координат задана неправильно.
Более подробно о картографических проекциях и системах координат
Для дальнейшего обсуждения, расстоянием всегда будет считаться минимальный интервал между двумя объектами.
Особые соображения
- Несколько объектов могут оказаться на одинаковом удалении от другого объекта. В таком случае один из равноудаленных объектов будет выбираться в качестве ближайшего случайным образом.
- Если один из объектов содержит другой или находится внутри другого объекта, расстояние между ними равно 0.
- Это означает, что если объект находится внутри полигона, расстояние между ним и окружающим его полигоном равно 0.
- Расстояние между двумя объектами равняется нулю всякий раз, когда у них имеется хотя бы одна общая координата x,y.
- Это означает, что при пересечении, перекрытии или касании двух объектов, расстояние между ними равняется 0.
- Расстояние всегда вычисляется до границы полигонального объекта, не до центра или центроида полигона.
- Как отмечено выше, если объект полностью находится внутри полигона, расстояние между ним и окружающим его полигоном равно 0.

- Как отмечено выше, если объект полностью находится внутри полигона, расстояние между ним и окружающим его полигоном равно 0.
- Расстояние между двумя объектами (любого типа) не меняется в зависимости от направления измерения.
Основные операции для определения расстояния
Вычисление расстояния зависит от типа геометрии объектов, а также от других факторов, таких как система координат. Однако есть три основных правила, подробнее описанные ниже, которые определяют способ вычисления расстояния.
- Расстояние между двумя точками является прямой линией, соединяющей их.
- Расстояние от точки до линии измеряется либо как перпендикуляр, либо как расстояние до ближайшей вершины.
- Расстояние между полилиниями определяется вершинами сегментов.
Правило 1: расстояние между двумя точками является прямой линией, соединяющей их
На рисунке ниже показано расстояние между двумя точками, вместе с несколькими ключевыми словами и объектами, использующимися инструментами близости.
Ключевые слова в вышеуказанных выносках (IN_FID, NEAR_DIST, NEAR_FID, NEAR_X, NEAR_Y и NEAR_ANGLE) являются полями, добавляемыми к выходным данным инструментами Построить таблицу ближайших объектов и , а также к входному классу объектов при использовании инструмента Ближайший объект.
Расстояние между мультиточками
Для особого случая, когда определяется расстояние между мультиточками, вычисляются расстояния от каждой точки входного мультиточечного объекта до каждой точки ближайшего мультиточечного объекта с помощью Правила 1, минимальное из этих трех расстояний станет расстоянием между мультиточечными объектами.
Кроме того, когда одна из точек мультиточечного объекта находится поверх одной из точек другого мультиточечного объекта, расстояние между ними равняется 0. Это справедливо для всех составных объектов.
Правило 2: расстояние от точки до полилинии измеряется либо как перпендикуляр, либо как расстояние до ближайшей вершины
В ArcGIS линейные объекты называются полилиниями. Эти два термина, линия и полилиния, взаимозаменяемы. Полилиния является упорядоченным набором точек, эти точки называются вершинами. An individual vertice is a vertex. Полилиния может иметь любое количество вершин. Линия, заданная двумя вершинами, называется сегментом. Две вершины, которые задают сегмент линии, называются конечными вершинами.
Две вершины, которые задают сегмент линии, называются конечными вершинами.
Сходным образом, полигон является замкнутой областью, заданной одной или несколькими полилиниями.
Кратчайшим расстоянием от точки до сегмента линии является перпендикуляр к ней. Если в пределах конечных вершин сегмента перпендикуляр провести не удается, кратчайшим расстоянием будет расстояние до ближайшей конечной вершины.
Расстояние от точки до полилинии
Если полилиния содержит только один сегмент, для вычисления расстояния применяется Правило 2.
Если полилиния состоит из нескольких сегментов (чаще всего), сначала определяется ближайший к точке сегмент линии, затем для вычисления расстояния применяется Правило 2.
Расстояние от точки до полигона
Поскольку полигон является замкнутой областью, образованной набором сегментов линий, вычисление расстояния от точки до полигона включает определение ближайшего к точке сегмента, затем применяется Правило 2.
Расстояние будет определяться, только если точка находится вне полигона; иначе, расстояние равно 0.
На рисунке выше, для точек 2 и 3 расстояние равно 0, для точек 1 и 4 – расстояние положительно.
Правило 3: расстояние между полилиниями определяется вершинами сегментов линии
Для двух объектов, не являющихся точками, таких как два сегмента линий:
- Расстояние вычисляется от каждой из конечных вершин входного сегмента до ближайшего сегмента с использованием Правила 2.
- Расстояние вычисляется от каждой из конечных вершин ближайшего сегмента до входного сегмента.
Расстояние от полилинии до полилинии
В простейшем случае, предположим, что оба полилинейных объекта состоят из одного сегмента. На рисунке ниже показан перпендикуляр CX от вершины C до сегмента, заданного вершинами AB. Перпендикуляр от вершины D также вычисляется, но это расстояние больше, чем расстояние CX. Поэтому CX является кратчайшим расстоянием от сегмента CD до сегмента AB.
Обратите внимание, что перпендикуляр от вершины A или B до сегмента CD провести нельзя, поэтому, кратчайшее расстояние вычисляется от вершин A и B до вершины C. В результате, именно AC является кратчайшим расстоянием между сегментами AB и CD.
Из двух вычисленных расстояний (AC и CX), CX является кратчайшим между двумя сегментами, поскольку это минимальное расстояние из всех расстояний между вершинами и сегментом.
Когда обе полилинии состоят из нескольких сегментов, определяются два наиболее близкорасположенных друг к другу сегмента, затем вычисляется расстояние, согласно Правилу 3.
Расстояние от полилинии до полигона
При вычислении расстояния между полилинией и полигоном определяются два наиболее близкорасположенных сегмента: один сегмент полилинии и один сегмент из образующих границу полигона. Расстояние между этими двумя сегментами определяется так же, как описано в Правиле 3.
Краткая информация
На следующем рисунке показано, как измеряется расстояние между объектами различных типов и определяется положение ближайших объектов.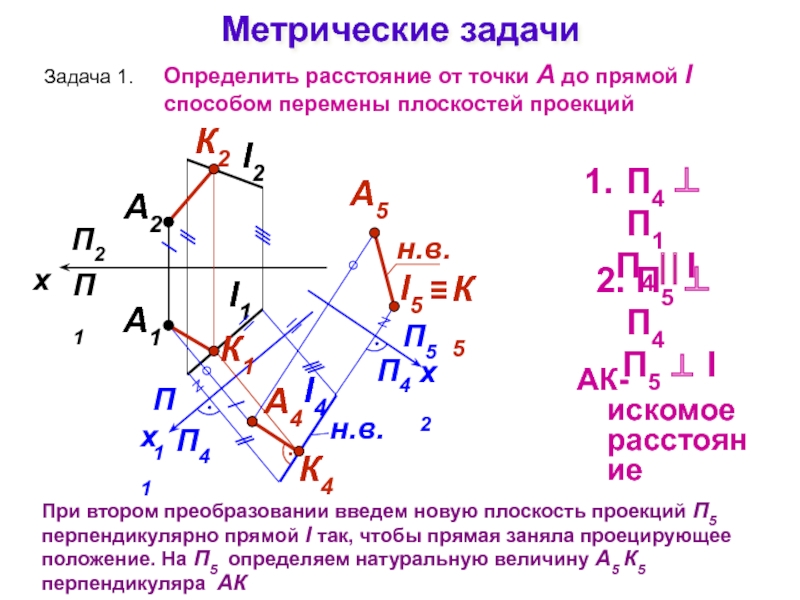 Показаны не все возможные комбинации.
Показаны не все возможные комбинации.
Связанные разделы
Отзыв по этому разделу?
Расчет расстояния от прямой до точки
| Уравнение прямой в различных видах |
| Общее уравнение прямой |
| Уравнение прямой с угловым коэффициентом |
| Уравнение прямой в отрезках |
| Нормальное уравнение прямой |
| Расстояние между заданной точкой и прямой составляет(в условных единицах) |
Расчет расстояния от прямой до точки
В школьной программе есть задачи на нахождение кратчайшего расстояния точки до прямой.
Прямая может быть задана или формулой или двумя координатами.
если прямая линия задана формулой то расчет растояния до точки (x1,y1)осуществляется по следующим формулам
Так как расстояние не может быть отрицательным, то знак + или — означает лишь следующее:
Значение положительно, если точка и начало координат лежат по разные стороны от прямой, и отрицательно, если по одну сторону.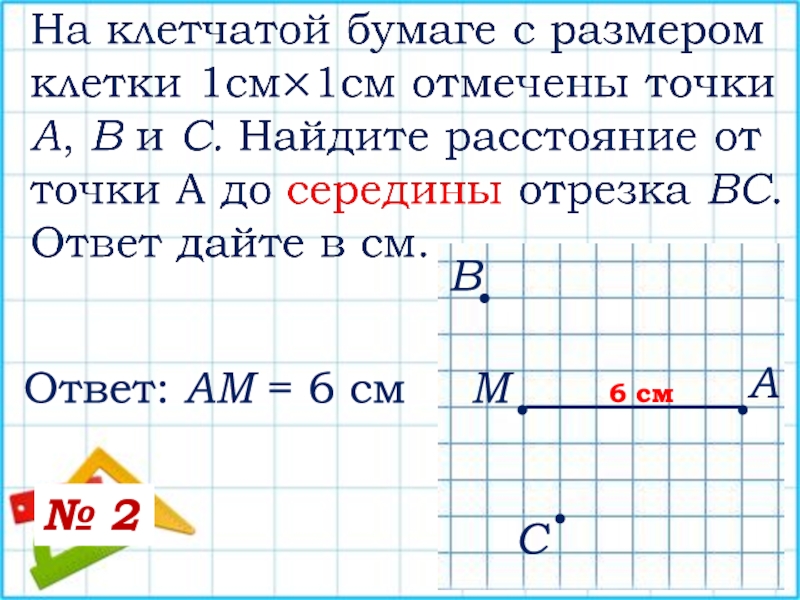
В принице, Вы можете воспользоваться универсальным определителем параметров прямой Расчет параметров прямой линии по заданным параметрам
Характеристики прямой могут быть достаточно разнообразны:
Прямую можно задать с помощью двух координат (xa:ya) и (xb:yb)
Можно задать в виде коэффициентов A, B и C прямой выраженной в виде
или в виде значений k и a прямой выраженной в виде
а также в любых других видах, в параметрическом или прямой в отрезках.
Точка с координатами (x0:y0) — это как раз та точка рассстояние между которой и прямой и надо определить.
Примеры
Найти расстояние между точкой с координатами (2:1) и прямой, проходящей через две точки: (2.38:2.98) и (-2.08:-1.74)
Логично предположить что нам известно
xa, xb, ya yb — это параметры прямой линии
а x0 и y0 — это координаты точки
так и запишем в запросе
line xa=2. 38;ya=2.98;xb=-2.08;yb=-1.74;x0=2;y0=1
38;ya=2.98;xb=-2.08;yb=-1.74;x0=2;y0=1
В ответе получаем
Параметры прямой линии по заданным параметрам
Общее уравнение Ax+By+C=0
Коэффициент А=4.72
Коэффициент B=-4.46
Коэффициент C=2.0572
Уравнение прямой в отрезках x/a+y/b = 1
Коэффициент a=-0.43584745762712
Коэффициент b=0.46125560538117
Уравнение прямой c угловым коэфициентом y = kx + b
Коэффициент k=1.0582959641255
Угол наклона к оси ( в градусах) f=46.622322587496
Нормальное уравнение прямой x*cos(q)+y*sin(q)-p = 0
Коэффициент p=-0.31679237157357
Коэффициент q=2. 3845093608736
3845093608736
Расстояние между точками=6.4938432380217
Расстояние от точки до прямой dp = -1.0836726021959
Таким образом наш ответ 1.0836726021959
Знак минус говорит о том, что начало координат и точка лежат по одну сторону от заданной прямой
Найти расстояние до точки (-4:-2) до прямой, заданная уравнением 3x+4y=5
Пишем следующий запрос
line x0=-4;y0=-2;A=3;B=4;C=-5
Получаем ответ
Параметры прямой линии по заданным параметрам
Общее уравнение Ax+By+C=0
Коэффициент А=3
Коэффициент B=4
Коэффициент C=-5
Уравнение прямой в отрезках x/a+y/b = 1
Коэффициент a=1.6666666666666
Коэффициент b=1.25
Уравнение прямой c угловым коэфициентом y = kx + b
Коэффициент k=-0. 75
75
Угол наклона к оси ( в градусах) f=-36.869897645844
Нормальное уравнение прямой x*cos(q)+y*sin(q)-p = 0
Коэффициент p=-0.99999999999998
Коэффициент q=0.92729521800162
Расстояние между точками=
Расстояние от точки до прямой dp = -4.9999999999999
Ответ на задачу = 4.9999999 то есть 5
и как можно убедиться на рисунке, точка начала кординат и заданная точка лежит тоже на одной стороне от заданной прямой
- Теорема Стюарта онлайн >>
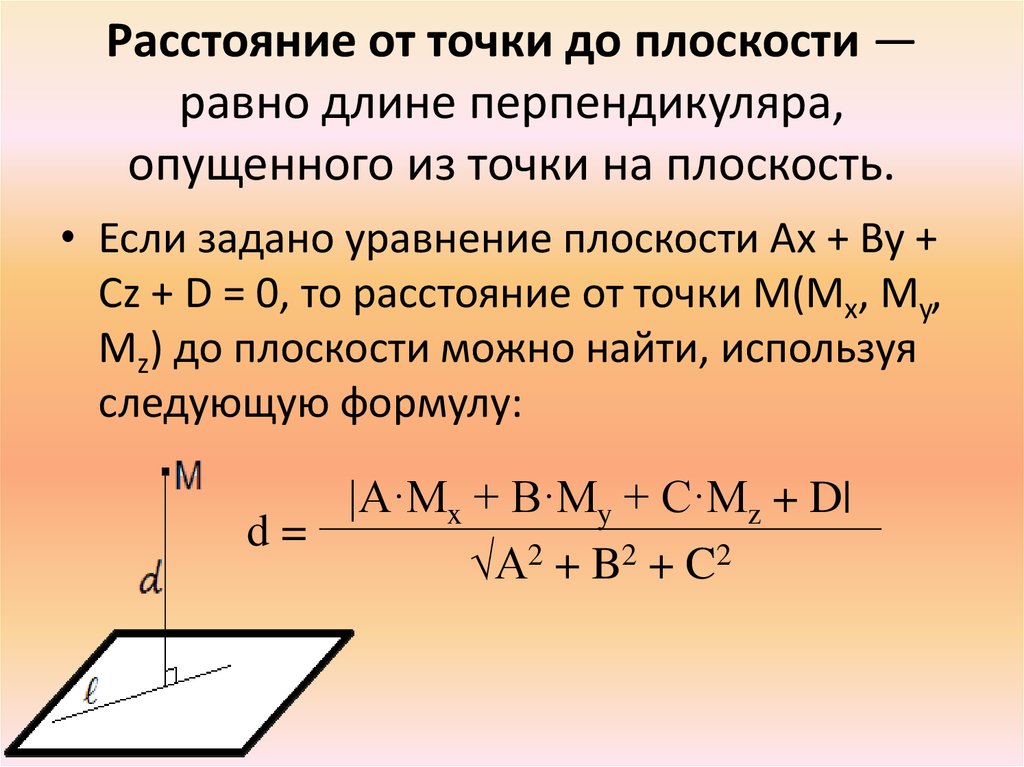
Определение расстояния от точки до плоскости
Расстояние от точки до плоскости равно длине перпендикуляра, опущенного из точки на плоскость, и в начертательной геометрии определяется графически согласно следующему алгоритму.
Алгоритм построения
- Плоскость переводят в проецирующее положение с помощью методов преобразования ортогональных проекций.

- Из точки на плоскость опускают перпендикуляр и находят его длину. Направление проекции перпендикуляра определяется на основании теоремы о проецировании прямого угла.
Задача № 1
Рассмотрим, как реализуется составленный нами алгоритм на практике. На рисунке ниже представлены графические построения, необходимые для определения расстояния между точкой N и плоскостью α, заданной треугольником ABC.
Ход решения
- Через вершину B» треугольника A»B»C» проводим проекцию h» горизонтали h. По линиям связи находим h’.
- Переводим ABC в проецирующее положение. Для этого перпендикулярно h вводим новую фронтальную плоскость П4. Проецируем на неё точку N и треугольник ABC.
- Из точки N»1 проводим N»1M»1 ⊥ A»1C»1. Длина отрезка N»1M»1 – искомое расстояние между плоскостью треугольника ABC и точкой N.
Задача № 2
Требуется определить величину расстояния между точкой K и плоскостью β, заданной следами.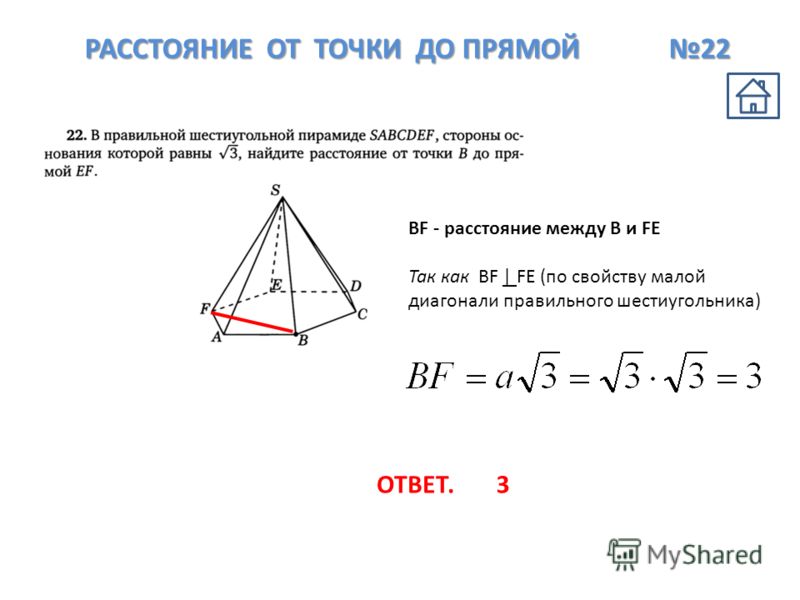 В отличие от предыдущей задачи здесь нет необходимости проводить линию уровня, так как её роль выполняет проекция h0β.
В отличие от предыдущей задачи здесь нет необходимости проводить линию уровня, так как её роль выполняет проекция h0β.
Ход решения
- Переводим плоскость β в проецирующее положение. Для этого перпендикулярно следу h0β вводим дополнительную фронтальную плоскость П4. На прямой f0β берем произвольную точку E, определяем её проекции E», E’ и E»1. Через E»1 и X0α1 проводим прямую f0β1, которая является следом плоскости β на П4. По линии связи определяем проекцию K»1 точки K.
- Из K»1 проводим перпендикуляр K»1M»1 в направлении прямой f0β1. Длина отрезка K»1M»1 – величина искомого расстояния от K до β.
Если требуется перевести отрезок KM в исходную систему плоскостей, то это делается с помощью обратных преобразований, как показано на следующем рисунке.
Похожие задачи:
Вычисление расстояния и начального азимута между двумя точками на сфере
Измерение расстояния и начального азимута между точками без проекционных преобразований
Длина дуги большого круга – кратчайшее расстояние между любыми двумя точками находящимися на поверхности сферы, измеренное вдоль линии соединяющей эти две точки (такая линия носит название ортодромии) и проходящей по поверхности сферы или другой поверхности вращения. Сферическая геометрия отличается от обычной Эвклидовой и уравнения расстояния также принимают другую форму. В Эвклидовой геометрии, кратчайшее расстояние между двумя точками – прямая линия. На сфере, прямых линий не бывает. Эти линии на сфере являются частью больших кругов – окружностей, центры которых совпадают с центром сферы.
Начальный азимут — азимут, взяв который при начале движения из точки А, следуя по большому кругу на кратчайшее расстояние до точки B, конечной точкой будет точка B. При движении из точки A в точку B по линии большого круга азимут из текущего положения на конечную точку B постоянно меняется. Начальный азимут [angles-rhumb.html отличен от постоянного], следуя которому, азимут из текущей точки на конечную не меняется, но маршрут следования
При движении из точки A в точку B по линии большого круга азимут из текущего положения на конечную точку B постоянно меняется. Начальный азимут [angles-rhumb.html отличен от постоянного], следуя которому, азимут из текущей точки на конечную не меняется, но маршрут следования
Через любые две точки на поверхности сферы, если они не прямо противоположны друг другу (то есть не являются антиподами), можно провести уникальный большой круг. Две точки, разделяют большой круг на две дуги. Длина короткой дуги – кратчайшее расстояние между двумя точками. Между двумя точками-антиподами можно провести бесконечное количество больших кругов, но расстояние между ними будет одинаково на любом круге и равно половине окружности круга, или pi*R, где R – радиус сферы.
расстояние большого кругаНа плоскости (в прямоугольной системе координат), большие круги и их фрагменты, как было упомянуто выше, представляют собой дуги во всех проекциях, кроме гномонической, где большие круги — прямые линии.
Форма Земли может быть описана как сфера, поэтому уравнения для вычисления расстояний на большом круге важны для вычисления кратчайшего расстояния между точками на поверхности Земли и часто используются в навигации.
Вычисление расстояния этим методом более эффективно и во многих случаях более точно, чем вычисление его для спроектированных координат (в прямоугольных системах координат), поскольку, во-первых, для этого не надо переводить географические координаты в прямоугольную систему координат (осуществлять проекционные преобразования) и, во-вторых, многие проекции, если неправильно выбраны, могу привести к значительным искажениям длин в силу особенностей проекционных искажений.
Известно, что более точно описывает форму Земли не сфера, а эллипсоид, однако в данной статье рассматривается вычисление расстояний именно на сфере, для вычислений используется сфера радиусом 6372795 метров, что может привести к ошибке вычисления расстояний порядка 0.
Существует три способа расчета сферического расстояния большого круга (подробнее).
[править] Сферическая теорема косинусов
В случае маленьких расстояний и небольшой разрядности вычисления (количество знаков после запятой), использование формулы может приводить к значительным ошибкам связанным с округлением. Графическое изображение формул здесь и далее — из Википедии.
— широта и долгота двух точек в радианах
— разница координат по долготе
— угловая разница
Для перевода углового расстояния в метрическое, нужно угловую разницу умножить на радиус Земли (6372795 метров), единицы конечного расстояния будут равны единицам, в которых выражен радиус (в данном случае — метры).
[править] Формула гаверсинусов
Используется, чтобы избежать проблем с небольшими расстояниями.
[править] Модификация для антиподов
Предыдущая формула также подвержена проблеме точек-антиподов, чтобы ее решить используется следующая ее модификация. 0.5
p4 = sl1*sl2
p5 = cl1*cl2*cdelta
p6 = p4 + p5
p7 = p3/p6
anglerad = (p7.atan).SetFormatPrecision (num)
0.5
p4 = sl1*sl2
p5 = cl1*cl2*cdelta
p6 = p4 + p5
p7 = p3/p6
anglerad = (p7.atan).SetFormatPrecision (num)
dist = anglerad*rad
‘вычисление начального азимута
x = (cl1*sl2) — (sl1*cl2*cdelta)
y = sdelta*cl2
z = (-y/x).ATan.AsDegrees
if (x < 0) then z = z+180 end
z = -(z + 180 mod 360 — 180).AsRadians
anglerad2 = z — ((2*pi)*((z/(2*pi)).floor))
angledeg = (anglerad2*180)/pi
‘возврат значений длины большого круга и начального азимута
distlist = {dist, angledeg}
return distlist
Для вызова процедуры расчета длин приведенной выше, можно также воспользоваться следующим скриптом, результатом его работы будет расчет длин между точкой testpont до всех точек активной темы вида и запись результата в поле Newdist атрибутивной таблицы этой темы:
atheme = av.getactivedoc.getactivethemes.get(0)
aftab = atheme.getftab
f_shape = aftab.findfield("Shape")
f_dist = aftab.findfield("dist")
f_ang = aftab.findfield("ang")
'testpoint - точка отсчета
testpoint = point. make(25.85, 55.15)
aftab.seteditable(true)
'для каждой точки темы до которых считают расстояния от точки отсчета
for each rec in aftab
pnts = {}
apoint = aftab.returnvalue(f_shape, rec)
pnts.add(apoint.getx)
pnts.add(testpoint.getx)
pnts.add(apoint.gety)
pnts.add(testpoint.gety)
'Вызов процедуры расчета расстояний
'"Calc-distance" - название скрипта с процедурой в проекте
param = av.run("Calc-distance", pnts)
aftab.setvalue(f_dist, rec, param.get(0))
aftab.setvalue(f_ang, rec, param.get(1))
end
aftab.seteditable(false)
make(25.85, 55.15)
aftab.seteditable(true)
'для каждой точки темы до которых считают расстояния от точки отсчета
for each rec in aftab
pnts = {}
apoint = aftab.returnvalue(f_shape, rec)
pnts.add(apoint.getx)
pnts.add(testpoint.getx)
pnts.add(apoint.gety)
pnts.add(testpoint.gety)
'Вызов процедуры расчета расстояний
'"Calc-distance" - название скрипта с процедурой в проекте
param = av.run("Calc-distance", pnts)
aftab.setvalue(f_dist, rec, param.get(0))
aftab.setvalue(f_ang, rec, param.get(1))
end
aftab.seteditable(false)
[править] Реализация на языке Python
Реализует полный вариант расчета через atan2(), более универсальнее, чем вариант для Avenue. (скачать скрипт)
import math #pi - число pi, rad - радиус сферы (Земли) rad = 6372795 #координаты двух точек llat1 = 77.1539 llong1 = -120.398 llat2 = 77.1804 llong2 = 129.55 #в радианах lat1 = llat1*math.pi/180. lat2 = llat2*math.pi/180. long1 = llong1*math.pi/180. long2 = llong2*math.pi/180. #косинусы и синусы широт и разницы долгот cl1 = math.cos(lat1) cl2 = math.cos(lat2) sl1 = math.sin(lat1) sl2 = math.sin(lat2) delta = long2 - long1 cdelta = math.cos(delta) sdelta = math.sin(delta) #вычисления длины большого круга y = math.sqrt(math.pow(cl2*sdelta,2)+math.pow(cl1*sl2-sl1*cl2*cdelta,2)) x = sl1*sl2+cl1*cl2*cdelta ad = math.atan2(y,x) dist = ad*rad #вычисление начального азимута x = (cl1*sl2) - (sl1*cl2*cdelta) y = sdelta*cl2 z = math.degrees(math.atan(-y/x)) if (x < 0): z = z+180. z2 = (z+180.) % 360. - 180. z2 = - math.radians(z2) anglerad2 = z2 - ((2*math.pi)*math.floor((z2/(2*math.pi))) ) angledeg = (anglerad2*180.)/math.pi print 'Distance >> %.0f' % dist, ' [meters]' print 'Initial bearing >> ', angledeg, '[degrees]'
[править] Реализация в Excel
Скачать пример расчета расстояния большого круга и начального азимута в Excel. Демонстрирует расчеты через закон косинусов, гаверсинус, полное уравнение и полное уравнение через atan2(). 0.5) * 6372795 End With End Function
0.5) * 6372795 End With End Function
[править] Проверочный набор данных
Если все считается правильно, должны быть получены следующие результаты (координаты точек даны как широта/долгота, расстояние в метрах, начальный угол в десятичных градусах):
| # | Точка 1 | Точка 2 | Расстояние | Угол |
| 1 | 77.1539/-139.398 | -77.1804/-139.55 | 17166029 | 180.077867811 |
| 2 | 77.1539/120.398 | 77.1804/129.55 | 225883 | 84.7925159033 |
| 3 | 77.1539/-120.398 | 77.1804/129.55 | 2332669 | 324.384112704 |
[править] Ссылки по теме
Расстояние от точки до отрезка
Расстоянием от точки до отрезка является либо перпендикуляр, опущенный из этой точки на отрезок, либо минимальное расстояние от точки до одного из концов отрезка.
Если треугольник, вершинами которого является данная точка и концы заданного отрезка, является тупоугольным (проверка на тупоугольность проводится рассмотрением знака скалярного произведения соответствующих векторов, построенных на сторонах треугольника (кос тупого угла отрицательный))(т. е. из данной точки невозможно опустить перпендикуляр на данный отрезок), то расстоянием от точки до отрезка считается минимальное расстояние от данной точки, до одного из концов отрезка. Оно определяется с помощью формулы:
((х1— х2)2 + (у1 — у2)2)-1/2.
Если все же перпендикуляр опустить возможно, то расстоянием от точки до отрезка считается длина этого перпендикуляра. Ее можно определить двумя способами:
1) посчитав площадь треугольника по двум формулам (полувысота на сторону и полупроизведение сторон на синус угла между ними) мы можем выразить высоту как:
h = (AC • AB • sin (AC, AB)) / BC ;
2) можем определить координаты точки пресечения отрезка с перепендикуляром, опущенным из данной точки на отрезок и посчитать расстояние между двумя точками. Для этого сначала нам надо найти уравнение перпендикуляра к данной прямой, проходящего через данную точку, затем решить систему уравнений (k и l — координаты вершины перпендикуляра, x1, y1, x2, y2 — координаты концов отрезка):
Для этого сначала нам надо найти уравнение перпендикуляра к данной прямой, проходящего через данную точку, затем решить систему уравнений (k и l — координаты вершины перпендикуляра, x1, y1, x2, y2 — координаты концов отрезка):
(1)(x — x1)(y2 — y1) = (y — y1)(x2 — x1)
(2) (x — k)(x2 — x1) = — (y — l)(y2 — y1)
Если (x2 — x1) = 0, то решение:
x = x1
y = l.
Если (y2 — y1) = 0, то решение:
y = y1
x = k.
В остальных случаях (пусть (x2 — x1) = α, (y2 — y1) = β):
x = (α / β) (y — y1) + x1
y = ((α2 / β)y1 + α (k — x1) + βl) / ((α2 / β) + β).
Калькулятор расстояний
Калькулятор расстояний Калькуляторы, представленные ниже, можно использовать для определения расстояния между двумя точками на двухмерной плоскости или трехмерном пространстве. Их также можно использовать для определения расстояния между двумя парами широты и долготы или двумя выбранными точками на карте.
Их также можно использовать для определения расстояния между двумя парами широты и долготы или двумя выбранными точками на карте.
2D-калькулятор расстояния
Используйте этот калькулятор, чтобы найти расстояние между двумя точками на 2D-координатной плоскости.
Трехмерный калькулятор расстояний
Используйте этот калькулятор, чтобы найти расстояние между двумя точками в трехмерном координатном пространстве.
Расстояние по широте и долготе
Используйте этот калькулятор, чтобы найти кратчайшее расстояние (большой круг / воздушное расстояние) между двумя точками на поверхности Земли.
Расстояние на карте
Щелкните карту ниже, чтобы установить две точки на карте и найти кратчайшее расстояние (большой круг / воздушное расстояние) между ними. После создания маркер (маркеры) можно переместить, щелкнув и удерживая, а затем перетащив их.
‘; calcResult + = »; } else if (markerCount> 0) { calcResult + = ‘Point 1: [‘ + lat1 + ‘,’ + lon1 + ‘]
Установите другой маркер на карте, чтобы рассчитать расстояние.
Установите два маркера на карте, чтобы рассчитать расстояние между ними.
‘; } calcResult + = »; gObj («mapresult»). innerHTML = calcResult; }Расстояние в системе координат
Расстояние в двухмерной координатной плоскости:
Расстояние между двумя точками на двухмерной координатной плоскости можно найти с помощью следующей формулы расстояния
d = √ (x 2 — x 1 ) 2 + (y 2 — y 1 ) 2
, где (x 1 , y 1 ) и (x 2 , y 2 ) — координаты двух задействованных точек.Порядок точек не имеет значения для формулы, если выбранные точки совпадают. Например, учитывая две точки (1, 5) и (3, 2), либо 3, либо 1 могут быть обозначены как x 1 или x 2 , если используются соответствующие значения y:
Использование (1, 5) как (x 1 , y 1 ) и (3, 2) как (x 2 , y 2 ):
| d = | √ (3-1) 2 + (2-5) 2 |
| = | √2 2 + (-3) 2 |
| = | √4 + 9 |
| = | √13 |
Использование (3, 2) как (x 1 , y 1 ) и (1, 5) как (x 2 , y 2 ):
| d = | √ (1-3) 2 + (5-2) 2 |
| = | √ (-2) 2 + 3 2 |
| = | √4 + 9 |
| = | √13 |
В любом случае результат один и тот же.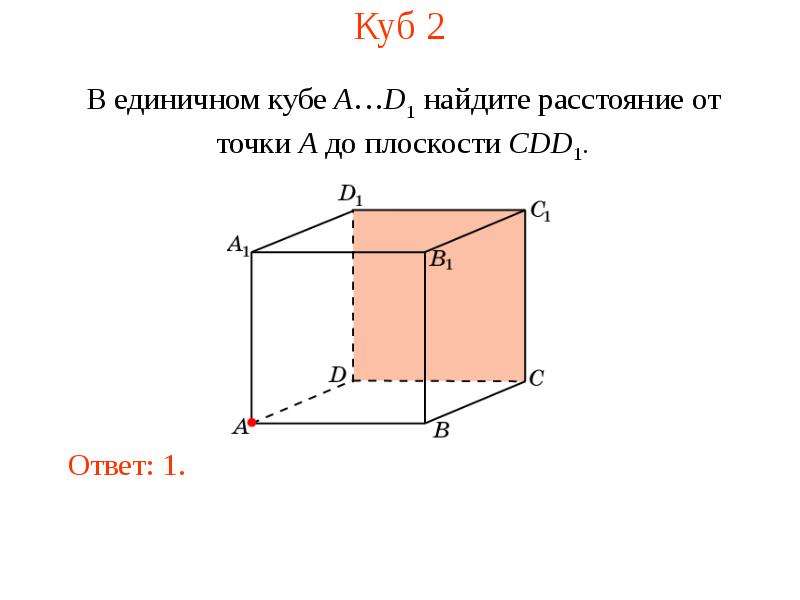
Расстояние в трехмерном координатном пространстве:
Расстояние между двумя точками на трехмерной координатной плоскости можно найти с помощью следующей формулы расстояния
d = √ (x 2 — x 1 ) 2 + (y 2 — y 1 ) 2 + (z 2 — z 1 ) 2
, где (x 1 , y 1 , z 1 ) и (x 2 , y 2 , z 2 ) — это трехмерные координаты двух задействованных точек.Как и в случае двухмерной версии формулы, не имеет значения, какая из двух точек обозначена (x 1 , y 1 , z 1 ) или (x 2 , y 2 , z 2 ), если в формуле используются соответствующие точки. Учитывая две точки (1, 3, 7) и (2, 4, 8), расстояние между точками можно найти следующим образом:
| d = | √ (2-1) 2 + (4-3) 2 + (8-7) 2 |
| = | √1 2 + 1 2 + 1 2 |
| = | √3 |
Расстояние между двумя точками на поверхности Земли
Есть несколько способов найти расстояние между двумя точками на поверхности Земли. Ниже приведены две общие формулы.
Ниже приведены две общие формулы.
Формула Хаверсина:
Формула гаверсинуса может использоваться, чтобы найти расстояние между двумя точками на сфере, учитывая их широту и долготу:
В формуле гаверсинуса d — это расстояние между двумя точками вдоль большого круга, r — радиус сферы, & directphi; 1 и & Stratocaster; 2 — это широты двух точек, а λ 1 и λ 2 — долготы двух точек, все в радианах.
Формула гаверсинуса работает, находя расстояние по большому кругу между точками широты и долготы на сфере, которое можно использовать для аппроксимации расстояния на Земле (поскольку оно в основном сферическое). Большой круг (также ортодромия) сферы — это самый большой круг, который можно нарисовать на любой данной сфере. Он образован пересечением плоскости и сферы через центральную точку сферы. Расстояние по дуге большого круга — это кратчайшее расстояние между двумя точками на поверхности сферы.
Результаты с использованием формулы гаверсинуса могут иметь погрешность до 0,5%, потому что Земля — не идеальная сфера, а эллипсоид с радиусом 6 378 км (3963 мили) на экваторе и радиусом 6 357 км (3950 миль). у столба. Из-за этого формула Ламберта (формула эллипсоидальной поверхности) более точно аппроксимирует поверхность Земли, чем формула гаверсинуса (формула сферической поверхности).
Формула Ламберта:
Формула Ламберта (формула, используемая вычислителями выше) — это метод, используемый для вычисления кратчайшего расстояния по поверхности эллипсоида.Когда он используется для аппроксимации Земли и расчета расстояния на поверхности Земли, он имеет точность порядка 10 метров на тысячи километров, что более точно, чем формула гаверсинуса.
Формула Ламберта выглядит следующим образом:
, где a — экваториальный радиус эллипсоида (в данном случае Земли), σ — центральный угол в радианах между точками широты и долготы (найденный с использованием такого метода, как формула гаверсинуса), f — сглаживание Земля, а также X и Y развернуты ниже.
Где P = (β 1 + β 2 ) / 2 и Q = (β 2 — β 1 ) / 2
В приведенных выше выражениях β 1 и β 1 представляют собой приведенные широты с использованием следующего уравнения:
загар (β) = (1 — f) загар (& Straightphi;)
, где & Stratocaster; широта точки.
Обратите внимание, что ни формула гаверсинуса, ни формула Ламберта не обеспечивают точное расстояние, потому что невозможно учесть все неровности на поверхности Земли.
Расчет расстояния от линии до точки, онлайн-калькулятор и формула
Онлайн-калькулятор для расчета расстояния между линией и точкой в системе координат
Рассчитать евклидово расстояние онлайн
На этой странице можно рассчитать расстояние между линией и точкой в системе координат.
Введите координаты X / Y линии и точки.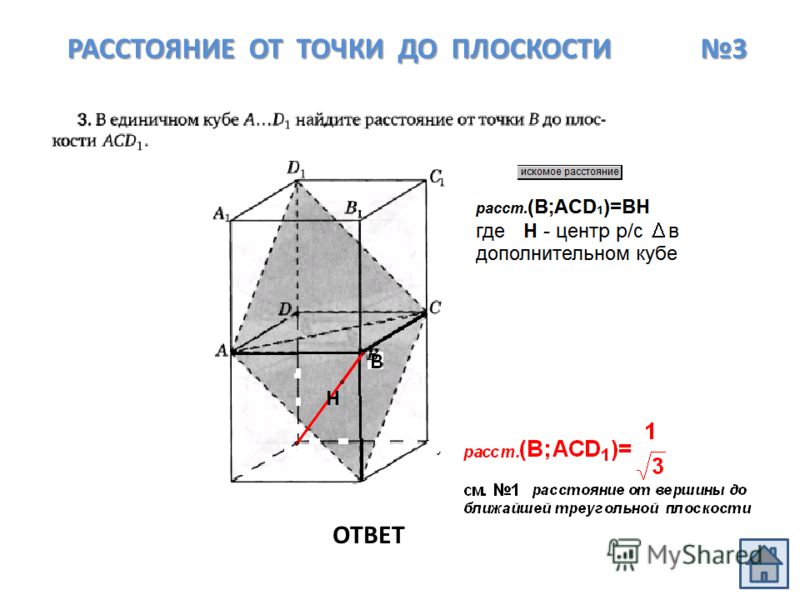 Неважно, какая точка линии первая, а какая вторая.
Результат будет таким же.
Неважно, какая точка линии первая, а какая вторая.
Результат будет таким же.
Вычисляется евклидово расстояние между этой линией и указанной точкой. Возвращает расстояние от бесконечной линии. Поэтому конечные точки указанной линии не учитываются в расчетах.
|
|
Измерение расстояния на карте
Инструмент измерения расстояния — это простой способ найти расстояние между двумя или более точками на карте.
Выберите скорость …
Или выберите вид транспорта …
Как использовать инструмент измерения расстояния
Просто щелкните один раз на одной точке, затем щелкните еще раз на второй точке. Затем должно отображаться расстояние. Вы можете щелкнуть более двух точек, чтобы построить непрерывный маршрут.
Используйте переключатель миль / км / морских миль / ярдов для измерения расстояний в км, милях или морских милях. Параметр «Автопанорамирование» перемещает карту по мере того, как вы щелкаете по точкам.
Текстовое поле «Поиск местоположения» позволяет быстро добраться до нужной области, не тратя время на масштабирование и панорамирование, чтобы найти ее. Например, если вы хотите найти город Рим в Италии, введите «Рим, Италия», а затем нажмите «Поиск». Затем карта переместится прямо в Рим. Обратите внимание на формат «[город] [запятая] [пробел] [округ]»
Переключение маркеров покажет или скроет маркеры, если они будут мешать
Очистить последнюю удаляет последнюю точку с карты
Увеличить по размеру: масштабирование и панорамирование карты для получения наилучшего соответствия всех ваших точек при максимально возможном увеличении
Очистить карту — это кнопка сброса, которая очищает все точки и позволяет снова начать измерение расстояния
Вы можете редактировать положение любых существующих точек, перетаскивая маркер (когда они отображаются) и бросая маркер в его новом положении
Вы также можете настроить высоту карты, чтобы она была большой, средней или маленькой.
Вы можете удалить точку, щелкнув узел
Будущие идеи и улучшения
- Автоматическое изменение маршрута для оптимального расстояния (задача коммивояжера)
- Есть другие скорости, например оптоволоконный кабель (~.6 c) и Mach
- Возможность добавления заголовка к маркеру, который затем появляется при наведении курсора мыши и экспорте данных
- Добавить байдарку в список видов транспорта
История версий
- 21 февраля 2021 — Выбранные единицы расстояния сохраняются и вызываются при следующем посещении
- 6 июля 2020 г. — Новая опция экспорта ссылки на маршрут. Находится в разделе параметров экспорта
- 2 июня 2019 — Исправлена ошибка, из-за которой не работал вывод счетчиков
- 29 мая 2019 — Реализованы листовки-карты
- 20 мая 2019 г. — Исправлена ошибка в браузере IE
- 9 мая 2019 г. — Исправлена ошибка, из-за которой расстояние не сбрасывалось до нуля при нажатии кнопки «Очистить карту».

- 14 сентября 2017 — Расстояние теперь отображается на карте в полноэкранном режиме
- , 4 августа 2017 г. — Переключатель единиц измерения обновлен.Футов добавлено
- 24 июля 2017 — Полноэкранный режим перенесен на карту. Теперь находится в правом верхнем углу
- , 4 июля 2017 г. — Исправлена проблема с экспортом CSV и XLSX
- 29 января 2017 г. — Возможность отображения карты высот и экспорта файла CSV с данными о высоте вдоль маршрута
- 25 ноября 2016 г. — экспорт KML для отображения контактов на каждом узле маршрута
- 23 ноября 2016 г. — добавлена опция загрузки KML, CSV и XLSX
- 19 июля 2016 г. — Исправлены ошибки, связанные с изменением вида транспорта и расчетного времени в пути при изменении единиц измерения
- 5 июля 2016 — Добавлены метры как единицы расстояния
- 25 июня 2016 — Единицы скорости движения меняются в зависимости от единиц расстояния
- , 20 июня 2016 г. — Исправлена ошибка, из-за которой количество дней отображалось в два раза больше фактического значения
- 24 марта 2016 — Точки маршрута теперь можно добавлять в середине пути.
 Очки также можно удалить, щелкнув правой кнопкой мыши
Очки также можно удалить, щелкнув правой кнопкой мыши - 25 января 2016 г. — Скорость теперь можно вводить вручную
- 28 декабря 2015 г. — Добавлена возможность переключения между минутами, часами и днями для оценки времени в пути
- 24 июня 2014 — Добавлена опция Привязка к дорогам
- 24 марта 2014 г. — Добавлена опция «Панорама до моего местоположения»
- 11 января 2012 г. — Реализован Google Maps API V3. Добавлен полноэкранный режим
- 12 октября 2010 г. — маркеры теперь показывают их широту и долготу при наведении на них курсора
- 15 октября 2009 г. — Добавлен вывод времени в пути
- 12 октября 2009 г. — Добавлена опция карты местности .
- 20 февраля 2008 г. — Обновленный дизайн теперь с перетаскиваемыми маркерами
- 1 ноября 2007 г. — Добавлено текстовое поле быстрого поиска
- 19 октября 2007 г. — Ярды добавлены в качестве единицы измерения
- 9 октября 2007 г. — добавлены морские мили в качестве единицы измерения
- 5 сентября 2007 г.
 — описательный текст обновлен
— описательный текст обновлен - 28 июня 2007 г. — Страница создана
Соответствующие ссылки
Если вы пытаетесь измерить расстояние между двумя городами, то инструмент «Как далеко между ними», вероятно, больше подходит для ваших нужд.
Расстояние между двумя точками на Земле Калькулятор
- Цель использования
- Определите расстояние между двумя точками, используя одинаковые числа для координат как в системе координат Индии 1975 года, так и в системе координат WGS84. Разница будет заключаться в ошибке при использовании координат датума 1975 года на карте WGS84; или исправление, необходимое для того, чтобы координаты 1975 года были «хорошими» на карте WGS84.
[1] 2021/06/07 23:25 60 лет и старше / Пенсионер / Очень /
- Цель использования
- Как далеко вы живете от места своего рождения?
[2] 2021.04.23 14:01 Уровень 30 лет / Учитель / Исследователь / Полезный /
- Цель использования
- Нахождение ответа на вопрос: «Какое самое дальнее место вы побывали? »
[3] 2021/04/06 03:45 Уровень 30 лет / Инженер / Очень /
- Цель использования
- Годзилла против Конга
[4] 2021/04/01 09:38 20-летний уровень / Средняя школа / Университет / аспирант / Очень /
- Цель использования
- Определение расстояния между городами
[5] 2021 / 15. 03.01 01:54 До 20 лет / Начальная школа / Неполная средняя школа / Полезно /
03.01 01:54 До 20 лет / Начальная школа / Неполная средняя школа / Полезно /
- Цель использования
- Вычислить ошибку между опубликованными координатами и координатами GPS.
[6] 2021/03/01 08:41 60 лет старый уровень или выше / Другое / Полезное /
- Цель использования
- Конечное расстояние для двух точек по сравнению с авиалайнером максимальная дальность, и посмотрите, осталось ли достаточно топлива, чтобы развернуться и вернуться в исходный аэропорт непосредственно перед посадкой
[7] 2021.01.15 12:51 Моложе 20 лет / Средняя школа / Университет / аспирант / Полезно /
- Цель использования
- вычислить расстояние между двумя точками в моем доморощенном мире с настраиваемым радиусом для наземных путешествий в Dungeons and Dragons
[8] 2020/12/06 06:37 20 лет уровень / Другое / Очень /
- Цель использования
- Чтобы узнать, как далеко от меня мой парень.
 9,250 миль 🙁
9,250 миль 🙁
[9] 2020/10/09 10:40 Уровень 30 лет / Учитель / Исследователь / Очень /
- Цель использования
- Базовое расстояние для расчета лунного параллакса
[10] 2020/09/10 18:26 Уровень 20 лет / Средняя школа / Университет / аспирант / Полезно /
Расчет расстояния между двумя точками на планете прямо на карте
На главную> Инструменты> Расстояние
Перетащите маркер на карту, чтобы рассчитать расстояние (км, метры, миля, фут) и азимутальный угол направления на карте Google между двумя точками земли.Расчет средней скорости или затраченного времени.
Вернуться к началу Содержание | скачать PDF-файл |
Наверх Содержание | скачать PDF-файл |
Содержание
Формат
Расчет расстояния между двумя географическими точками
Расчет направления между двумя географическими точками
Расчет пункта назначения
Определить скорость или истекшее время
Комментарий
Вернуться наверх Содержание | скачать PDF-файл |Формат
Диапазон значений
Допустимое значение широты от -90. От 0 ° до 90,0 ° для долготы от -180,0 ° до 180,0 °, знак + следует опустить, а знак минус не требуется, если есть радиокомпонент для выбора направления NS или WE (градусы и десятичный формат) .
От 0 ° до 90,0 ° для долготы от -180,0 ° до 180,0 °, знак + следует опустить, а знак минус не требуется, если есть радиокомпонент для выбора направления NS или WE (градусы и десятичный формат) .Десятичное число
Вы должны выбрать направление (С-Ю или З-В) и вставить число от 0 до 90 для широты или от 0 до 180 для долготы (например, 45.12345).градусов Формат
градусов состоит из направления (север-юг или запад-восток) и трех наборов чисел, разделенных символами для градусов (°), минут (’) и секунд («).Градус — это целое число без знака, от 0 до 90 для широты или от 0 до 180 для долготы. Минуты — это целое число без знака, от 0 до 59. Секунды — это двойное значение без знака, от 0 (или 0,0000) до 59,9999.
Координаты
Формат координат — это пара широты и долготы со знаком минус (-) для направления южная широта и западная долгота, разделенных запятой (,), вот пример:52.5163, 13.3779
40.7682, -73.9816
-22.9708, -43.1830
Поиск на карте
Щелкните поиск, чтобы открыть веб-страницу «Координаты Земли», здесь вы можете получить широту и долготу, просто щелкнув карту, и сохраните значение, нажав кнопку «Сохранить».
Вернуться к началу Содержание | скачать PDF-файл |
Расчет расстояния между двумя географическими точками
Формула, используемая для определения кратчайшего расстояния между двумя точками на суше (геодезическая), приближает геоид к сфере радиуса R = 6372.795477598 км (радиус квадратичной среды), поэтому расчет может иметь ошибку расстояния 0,3%, особенно в полярных крайних точках, и для больших расстояний через различные параллели. Учитывая две точки A и B на сфере, выраженные широтой (lat) и долготой (lon), вы получите:distance (A, B) = R * arccos (sin (latA) * sin (latB) + cos (latA) * cos (latB) * cos (lonA-lonB))
Используемые углы выражены в радианах, преобразование между градусами и радианами получается путем умножения угла на пи и деления на 180.
Вернуться к началу Содержание | скачать PDF-файл |
Расчет направления между двумя географическими точками
Чтобы определить направление от начальной точки между двумя точками на земле, используйте следующую формулу: Δφ = ln (tan (широта B /2 + π / 4) / tan (широта A /2 + π / 4))
Δlon = абс. (Длина A — длина B )
Подшипник
(Длина A — длина B )
Подшипник
: θ = atan2 (Δlon, Δφ)
Примечание: 1) ln = натуральный логарифм 2) если Δlon> 180 °, то Δlon = Δlon (mod 180).
3) операция a mod n 4) функция atan2 (y, x) 5) углы указаны в радианах
Вернуться к началу Содержание | скачать PDF-файл |
Расчет пункта назначения
Чтобы определить точку назначения, зная начальную точку, направление θ и расстояние d, мы используем следующую формулу: lat B = asin (sin (lat A ) * cos (d / R) + cos (lat A ) * sin (d / R) * cos (θ))
lon B = lon A + atan2 (sin (θ) * sin (d / R) * cos (lat A ), cos (d / R) — sin (lat A ) * sin ( шир. B ))
Примечание: 1) функция atan2 (y, x) 2) углы указаны в радианах.
Вернуться к началу Содержание | скачать PDF-файл |
Определить скорость или истекшее время
После расчета расстояния между двумя точками вы получите скорость, если нам известно время, затраченное на поездку из точки A в точку B.
Введите прошедшее время в формате чч: мм: сс, чтобы получить среднюю скорость.
Если вы знаете конечную точку и среднюю скорость, вы можете узнать время, чтобы добраться до точки B.
Вы можете ввести время в точке A и точке B, чтобы получить среднюю скорость.
Вернуться к началу Содержание | скачать PDF-файл |
Комментарий
Если вы обнаружили ошибку или другую неточность, хотите предложить новую функцию или просто высказать мнение о сайте, не стесняйтесь сделать это в следующем разделе «Комментарии» (или напрямую по электронной почте).Администраторы сайта ценят все комментарии, поскольку мы стремимся создавать точный и конструктивный ресурс.Заранее благодарим за ваш вклад в улучшение этого сайта (исправьте грамматические и переводные ошибки).
Вернуться к началу Содержание | скачать PDF-файл |
Как инструменты приближения вычисляют расстояние — ArcGIS Pro
Как определяется расстояние
Расстояние между любыми двумя объектами рассчитывается как кратчайшее расстояние между ними, то есть место, где два объекта находятся ближе всего друг к другу. Эта логика применяется к любому инструменту геообработки, который вычисляет расстояние, включая такие инструменты, как Ближайшая, Генерация ближней таблицы и Пространственное соединение (с параметром БЛИЖАЙШЕЕ совпадение).
Эта логика применяется к любому инструменту геообработки, который вычисляет расстояние, включая такие инструменты, как Ближайшая, Генерация ближней таблицы и Пространственное соединение (с параметром БЛИЖАЙШЕЕ совпадение).
Измерения расстояния будут наиболее точными, если входные данные находятся в эквидистантной системе координат проекции. Хотя расчеты расстояния всегда могут выполняться независимо от системы координат, результаты могут быть неточными или даже бессмысленными, если ваши данные находятся в географической системе координат или неправильно выбранной системе координат проекции.
Узнайте больше о системах координат и проекциях
В приведенном ниже обсуждении под расстоянием всегда понимается наименьшее расстояние между двумя объектами.
Особые соображения
- Несколько функций могут быть одинаково близки к другой функции. Когда это происходит, один из ближайших объектов случайным образом выбирается как самый близкий.

- Когда один объект содержит или находится внутри другого объекта, расстояние между ними равно нулю.
- Это означает, что когда объект находится внутри полигона, расстояние между объектом и окружающим его полигоном равно нулю.
- Расстояние между двумя объектами равно нулю, если между ними есть хотя бы одна координата x, y.
- Это означает, что когда два объекта пересекаются, перекрываются, пересекаются или касаются друг друга, расстояние между ними равно нулю.
- Расстояние всегда рассчитывается до границы полигонального объекта, а не до центра или центроида полигона.
- Как отмечалось выше, если объект полностью находится внутри многоугольника, расстояние между объектом и окружающим многоугольником равно нулю.
- Расстояние между двумя объектами (любого типа) всегда одинаково, независимо от того, до и от какого из них измеряется.

Основные операции для поиска расстояния
Расчет расстояния зависит от типа геометрии пространственных объектов, а также от других факторов, таких как система координат. Однако есть три основных правила, подробно описанных ниже, которые определяют, как рассчитывается расстояние.
- Расстояние между двумя точками — это прямая линия, соединяющая точки.
- Расстояние от точки до линии — это либо перпендикуляр, либо ближайшая вершина.
- Расстояние между полилиниями определяется вершинами сегментов.
Правило 1. Расстояние между двумя точками — это прямая линия, соединяющая точки
На следующем рисунке показано расстояние между двумя точками вместе с несколькими другими ключевыми словами и функциями, используемыми инструментами приближения.
Ключевые слова в выносках выше (IN_FID, NEAR_DIST, NEAR_FID, NEAR_X, NEAR_Y и NEAR_ANGLE) — это поля, добавляемые к выходным данным с помощью инструментов «Создать ближайшую таблицу» и инструментов, а также к входному классу пространственных объектов при запуске инструмента «Рядом».
Многоточечный — многоточечный
Для особого случая расчета расстояний между многоточечными точками расстояния от каждой точки входного многоточечного объекта до каждой точки ближайшего многоточечного объекта вычисляются с использованием правила 1, и наименьшее из этих расстояний — это расстояние между две многоточечные функции.
Кроме того, когда одна из точек многоточечного соединения находится над одной из точек другого многоточечного объекта, расстояние между двумя объектами многоточечного соединения равно нулю.Это относится ко всем составным объектам.
Правило 2: Расстояние от точки до полилинии — это перпендикуляр или ближайшая вершина
В ArcGIS линейные объекты называются полилиниями. Эти два термина, линия и полилиния, взаимозаменяемы. Полилиния — это упорядоченный набор точек, которые называются вершинами. Отдельная вершина — это вершина. Полилиния может иметь любое количество вершин. Линия, определяемая двумя вершинами, называется отрезком линии или отрезком.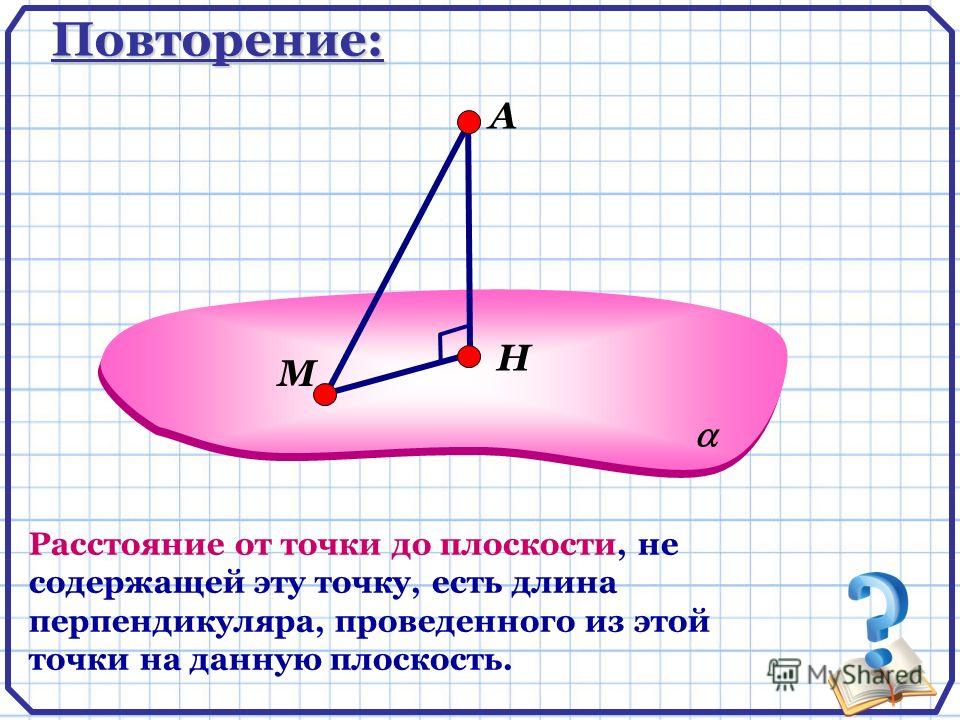 Две вершины, определяющие отрезок прямой, называются конечными вершинами.
Две вершины, определяющие отрезок прямой, называются конечными вершинами.
Точно так же многоугольник — это замкнутая область, определяемая одной или несколькими полилиниями.
Кратчайшее расстояние от точки до сегмента линии — это перпендикуляр к сегменту линии. Если перпендикуляр не может быть проведен внутри конечных вершин отрезка прямой, то расстояние до ближайшей конечной вершины является кратчайшим.
Точка к полилинии
Если полилиния имеет только один линейный сегмент, для получения расстояния применяется Правило 2.
Когда полилиния состоит из нескольких сегментов (наиболее распространенный случай), сначала определяется ближайший к точке сегмент, а затем применяется Правило 2 для получения расстояния.
Точка к многоугольнику
Поскольку многоугольник — это область, окруженная упорядоченным набором линейных сегментов, вычисление расстояния от точки до многоугольника включает в себя определение ближайшего линейного сегмента к точке, а затем применяется Правило 2 для получения расстояние.
Расстояние положительно, только если точка находится за пределами многоугольника; в противном случае он равен нулю.
На приведенном выше рисунке расстояние равно нулю для точек 2 и 3 и положительно для точек 1 и 4.
Правило 3: Расстояние между полилиниями определяется вершинами линейных сегментов
Для двух неточечных объектов, таких как два отрезка линии:
- Расстояние от каждой конечной вершины входного сегмента до ближайшего сегмента рассчитывается с использованием правила 2.
- Вычисляется расстояние от каждой из конечных вершин ближнего сегмента до входного сегмента.
Полилиния в полилинию
В простейшем случае предположим, что у обоих полилиний есть по одному сегменту. На рисунке ниже показан перпендикуляр CX от вершины C к отрезку, определяемому вершинами AB. Перпендикуляр к вершине D также может быть вычислен, но его расстояние больше, чем CX. Таким образом, CX — это кратчайшее расстояние от сегмента CD до сегмента AB.
Таким образом, CX — это кратчайшее расстояние от сегмента CD до сегмента AB.
Обратите внимание, что от вершины A или B к сегменту CD нельзя провести перпендикуляр, поэтому кратчайшее расстояние вычисляется от вершин A и B до вершины C.В результате AC — это кратчайшее расстояние от сегмента AB до сегмента CD.
Из двух вычисленных расстояний (AC и CX) CX — это кратчайшее расстояние между двумя сегментами, так как это наименьшее из всех расстояний между вершинами и сегментами.
Когда обе полилинии состоят из нескольких сегментов, обнаруживаются два ближайших сегмента, тогда расстояние между ними рассчитывается в соответствии с Правилом 3.
Полилиния до многоугольника
При вычислении расстояния между полилинией и многоугольником два ближайших сегмента вычисляются. определены: один от ломаной линии, а другой от последовательности сегментов, составляющих границу многоугольника.Расстояние между этими двумя сегментами рассчитывается в соответствии с процессом, описанным в Правиле 3.
Сводка
Следующая диаграмма дает общую картину того, как рассчитываются расстояния между различными типами объектов и где находятся ближайшие местоположения. может быть таким, как описано выше. Показаны не все возможные комбинации.
Связанные темы
Отзыв по этой теме?
Расстояние между двумя точками: определение, формулы и примеры
Мы в Cuemath считаем, что математика — это жизненный навык.Наши эксперты по математике сосредотачиваются на том, «почему» стоит за «что». Учащиеся могут исследовать огромное количество интерактивных листов, наглядных пособий, симуляторов, практических тестов и многого другого, чтобы глубже понять концепцию.
Забронируйте БЕСПЛАТНОЕ пробное занятие сегодня! и поучаствуйте в онлайн-классе Cuemath LIVE вместе со своим ребенком.
Определение расстояния между двумя точками Расстояние между любыми двумя точками — это длина отрезка линии, соединяющего точки.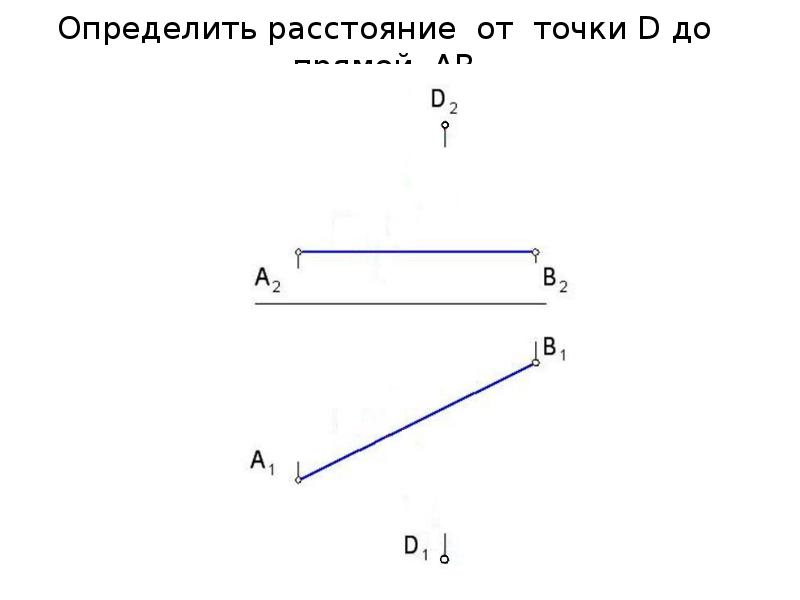 2} \]
2} \]
Это называется формулой расстояния .
Давайте теперь узнаем, как вывести эту формулу.
Формула доказательства расстояния
Предположим, что:
\ [A = (x_1, y_1) \\ [0,2 см] B = (x_2, y_2) \]
Далее предположим, что \ (\ overline {AB} = d \)
Теперь мы нанесем данные точки на координатную плоскость и соединим их линией.
Затем мы построим прямоугольный треугольник с гипотенузой \ (\ overline {AB} \).2} \]
(i) ось x равна \ (| b | \)
(ii) ось y равна \ (| a | \)
Здесь , мы использовали знаки абсолютного значения, потому что расстояние никогда не может быть отрицательным.
Помогите своему ребенку набрать больше баллов с помощью запатентованного БЕСПЛАТНОГО диагностического теста Cuemath. Получите доступ к подробным отчетам, индивидуальным планам обучения и БЕСПЛАТНОЙ консультации. Попытайтесь пройти тест сейчас.
Попытайтесь пройти тест сейчас.
Решенные примеры
Найдите расстояние между двумя точками \ ((2, -6 \)) и \ ((7, 3 \))
Решение:
Предположим, что данные точки равны:
\ [\ begin {align} (x_1, y_1) & = (2, -6) \\ [0.2} \\ [0,3 см] d & = \ sqrt {25 + 81} \\ [0,3 см] d & = \ sqrt {106} \ end {align} \]
| \ (\ следовательно \) Расстояние \ (= \ sqrt {106} \) |
Покажите, что точки \ ((2, -1), (0, 1) \) и \ ((2, 3 \)) являются вершинами прямоугольного треугольника.
Решение:
Предположим, что данные точки равны:
\ [\ begin {align} A & = (2, -1) \\ [0,2 см] B & = (0,1) \\ [0.2 \\ [0,3 см] 8 + 8 & = 16 \\ [0,3 см] 16 & = 16 \ конец {выровнено} \]
Таким образом, \ (A, B \) и \ (C \) удовлетворяют теореме Пифагора.
Итак, \ (\ треугольник ABC \) прямоугольный треугольник.
Мы можем доказать то же самое, отметив все координаты на графике:
Таким образом,
| Данные точки образуют прямоугольный треугольник. |
Найдите точку на оси Y, которая равноудалена от точек \ ((- 1, 2 \)) и \ ((2, 3) \)
Решение:
Мы знаем, что координата x любой точки на оси y равна \ (0 \)
Следовательно, мы считаем точку, равноудаленную от данных точек, равной \ ((0, k \)).2-6k \\ 2k & = 8 \\ k & = 4 \ end {align} \]
Следовательно, требуемая точка \ ((0, k) = (0, 4) \)
| \ (\ следовательно \) Обязательная точка \ (= (0, 4) \) |
Калькулятор расстояния между двумя точками
Вот «Калькулятор расстояния между двумя точками».
Здесь вы можете ввести координаты двух точек, и он покажет вам расстояние между ними с пошаговым объяснением.
CLUEless по математике? Узнайте, как CUEMATH Учителя объяснят вашему ребенку расстояние между двумя точками , используя интерактивные симуляции и рабочие листы, чтобы им больше никогда не приходилось запоминать что-либо по математике!
Изучите интерактивные и персонализированные онлайн-классы Cuemath, которые сделают вашего ребенка экспертом по математике. Забронируйте БЕСПЛАТНОЕ пробное занятие сегодня!
Практические вопросы
Сложные вопросы
- Вершинами прямоугольника являются \ ((- 4, -3), (4, -3), (4, 3), \) и \ ((- 4, 3) \).Какая у него площадь?
- Вершины прямоугольного треугольника — это \ ((- 3, 6), (1, 6) \) и \ ((1, -1) \).
 Какая у него площадь?
Какая у него площадь?
IMO (Международная олимпиада по математике) — это конкурсный экзамен по математике, который ежегодно проводится для школьников. Он побуждает детей развивать свои навыки решения математических задач с точки зрения соревнований.
Вы можете БЕСПЛАТНО скачать образцы работ по оценкам ниже:
Чтобы узнать больше об олимпиаде по математике, вы можете нажать здесь
Часто задаваемые вопросы (FAQ)
1.Каково определение расстояния между двумя точками?
Расстояние между любыми двумя точками — это длина отрезка линии, соединяющего точки.
Например, если \ (A \) и \ (B \) — две точки, и если \ (\ overline {AB} = 10 \) см, это означает, что расстояние между \ (A \) и \ (B \ ) составляет \ (10 \) см.
2. Какова формула расстояния между двумя точками?
Расстояние \ (d \) между двумя точками с координатами \ ((x_1, y_1) \) и \ ((x_2, y_2 \)) составляет:
| \ [d = \ sqrt {(x_2-x_1) ^ 2 + (y_2-y_1) ^ 2} \] |
Это называется формулой расстояния .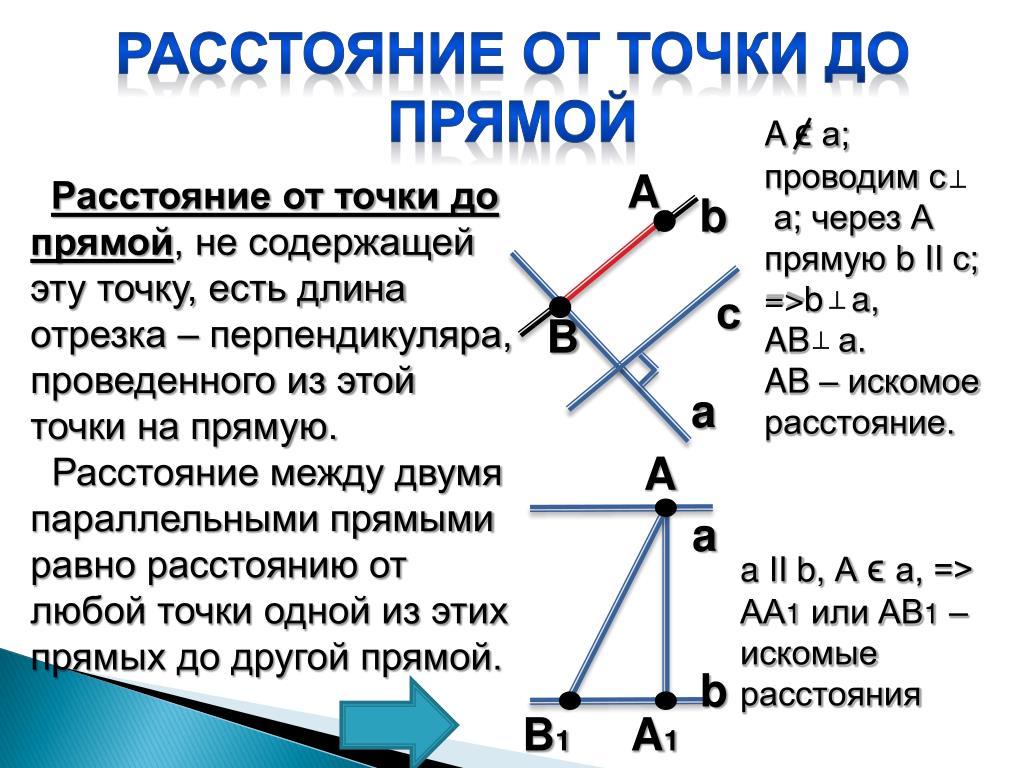



 make(25.85, 55.15)
aftab.seteditable(true)
'для каждой точки темы до которых считают расстояния от точки отсчета
for each rec in aftab
pnts = {}
apoint = aftab.returnvalue(f_shape, rec)
pnts.add(apoint.getx)
pnts.add(testpoint.getx)
pnts.add(apoint.gety)
pnts.add(testpoint.gety)
'Вызов процедуры расчета расстояний
'"Calc-distance" - название скрипта с процедурой в проекте
param = av.run("Calc-distance", pnts)
aftab.setvalue(f_dist, rec, param.get(0))
aftab.setvalue(f_ang, rec, param.get(1))
end
aftab.seteditable(false)
make(25.85, 55.15)
aftab.seteditable(true)
'для каждой точки темы до которых считают расстояния от точки отсчета
for each rec in aftab
pnts = {}
apoint = aftab.returnvalue(f_shape, rec)
pnts.add(apoint.getx)
pnts.add(testpoint.getx)
pnts.add(apoint.gety)
pnts.add(testpoint.gety)
'Вызов процедуры расчета расстояний
'"Calc-distance" - название скрипта с процедурой в проекте
param = av.run("Calc-distance", pnts)
aftab.setvalue(f_dist, rec, param.get(0))
aftab.setvalue(f_ang, rec, param.get(1))
end
aftab.seteditable(false)
 pi/180.
#косинусы и синусы широт и разницы долгот
cl1 = math.cos(lat1)
cl2 = math.cos(lat2)
sl1 = math.sin(lat1)
sl2 = math.sin(lat2)
delta = long2 - long1
cdelta = math.cos(delta)
sdelta = math.sin(delta)
#вычисления длины большого круга
y = math.sqrt(math.pow(cl2*sdelta,2)+math.pow(cl1*sl2-sl1*cl2*cdelta,2))
x = sl1*sl2+cl1*cl2*cdelta
ad = math.atan2(y,x)
dist = ad*rad
#вычисление начального азимута
x = (cl1*sl2) - (sl1*cl2*cdelta)
y = sdelta*cl2
z = math.degrees(math.atan(-y/x))
if (x < 0):
z = z+180.
z2 = (z+180.) % 360. - 180.
z2 = - math.radians(z2)
anglerad2 = z2 - ((2*math.pi)*math.floor((z2/(2*math.pi))) )
angledeg = (anglerad2*180.)/math.pi
print 'Distance >> %.0f' % dist, ' [meters]'
print 'Initial bearing >> ', angledeg, '[degrees]'
pi/180.
#косинусы и синусы широт и разницы долгот
cl1 = math.cos(lat1)
cl2 = math.cos(lat2)
sl1 = math.sin(lat1)
sl2 = math.sin(lat2)
delta = long2 - long1
cdelta = math.cos(delta)
sdelta = math.sin(delta)
#вычисления длины большого круга
y = math.sqrt(math.pow(cl2*sdelta,2)+math.pow(cl1*sl2-sl1*cl2*cdelta,2))
x = sl1*sl2+cl1*cl2*cdelta
ad = math.atan2(y,x)
dist = ad*rad
#вычисление начального азимута
x = (cl1*sl2) - (sl1*cl2*cdelta)
y = sdelta*cl2
z = math.degrees(math.atan(-y/x))
if (x < 0):
z = z+180.
z2 = (z+180.) % 360. - 180.
z2 = - math.radians(z2)
anglerad2 = z2 - ((2*math.pi)*math.floor((z2/(2*math.pi))) )
angledeg = (anglerad2*180.)/math.pi
print 'Distance >> %.0f' % dist, ' [meters]'
print 'Initial bearing >> ', angledeg, '[degrees]'

 Очки также можно удалить, щелкнув правой кнопкой мыши
Очки также можно удалить, щелкнув правой кнопкой мыши — описательный текст обновлен
— описательный текст обновлен 9,250 миль 🙁
9,250 миль 🙁
 Какая у него площадь?
Какая у него площадь?