Расстояние от а до б: Sorry, this page can’t be found.

Расстояние от дома до забора \ Акты, образцы, формы, договоры \ Консультант Плюс

]]>

Подборка наиболее важных документов по запросу Расстояние от дома до забора (нормативно–правовые акты, формы, статьи, консультации экспертов и многое другое).

Судебная практика: Расстояние от дома до забора Открыть документ в вашей системе КонсультантПлюс:
Подборка судебных решений за 2018 год: Статья 60 «Восстановление положения, существовавшего до нарушения права на земельный участок, и пресечение действий, нарушающих право на земельный участок или создающих угрозу его нарушения» ЗК РФ
(ООО юридическая фирма «ЮРИНФОРМ ВМ»)Принимая решение об устранении препятствий в пользовании земельным участком путем демонтажа возведенного сплошного ограждения на границе земельного участка истца и изменения конструкции крыши жилого дома с пристроем, суд в порядке пункта 1 статьи 40, пункта 1 статьи 43, пункта 2 статьи 60 ЗК РФ установил, что при возведении на садовом участке ответчика жилого дома с пристроем, в том числе по отношению к смежному земельному участку, принадлежащему истцу, нарушены нормативные требования о расстоянии от забора до дома, расположенного на земельном участке, часть конструкций забора между участками сторон не соответствует предусмотренным требованиям, возведенный ответчиком забор также не соответствует установленным требованиям, является сплошным и превышает нормативную высоту. Открыть документ в вашей системе КонсультантПлюс:
Подборка судебных решений за 2020 год: Статья 60 «Восстановление положения, существовавшего до нарушения права на земельный участок, и пресечение действий, нарушающих право на земельный участок или создающих угрозу его нарушения» ЗК РФ
(ООО юридическая фирма «ЮРИНФОРМ ВМ»)Руководствуясь статьей 60 Земельного кодекса РФ и установив, что стороны являются собственниками смежных земельных участков; в соответствии с актами обследования земельного участка выявлено, что на меже с соседним домовладением установлен забор на расстоянии 20 см от жилого дома, высотой 1,9 м, шириной зазора 0,1 — 0,5 см, чем нарушена инсоляция земельного участка истца; кроме того, со стороны домовладения ответчика вплотную к забору и на всю его высоту беспорядочно складирован строительный мусор (железные листы, шифер, доски, блоки и т.

п.), апелляционный суд отказал в обязании устранить нарушение прав истца в виде демонтажа дровяника, поскольку каких-либо доказательств, свидетельствующих о том, что имеющиеся у ответчика дрова складированы выше 2-метрового забора, истцом не представлено; представленные в материалы дела фотоматериалы доводы истца не подтверждают.

Статьи, комментарии, ответы на вопросы: Расстояние от дома до забора Открыть документ в вашей системе КонсультантПлюс:
Статья: Снос дачных коттеджей: споры. На земле СНТ
(Тихонова Н.)
(«Жилищное право», 2020, N 3)Кроме того, с иском о сносе самовольной постройки могут обратиться смежные землепользователи в связи с несоблюдением минимальных расстояний от забора до коттеджа, между домами, затемнением коттеджем земельного участка и невозможности использования соседями участка по назначению. Приведу в пример один из споров. З. обратилась в суд с иском к Г. об устранении препятствий в пользовании земельным участком, сносе самовольной постройки. В обоснование требований указано, что истец является собственником земельного участка, собственником смежного земельного участка в этом же СНТ является ответчик. Границы земельных участков установлены в 2003 году. В период с 2015 — 2016 года Г. возвела пристройку к жилому дому (баню) и сплошной забор, которые не соответствуют требованиям строительных норм и правил, поскольку забор из профлиста и частично пристройка располагаются за пределами границ земельного участка, принадлежащего ответчику, а именно на землях общего пользования и участке истца. Решением Чкаловского районного суда г. Екатеринбурга от 31.10.2017 частично удовлетворены исковые требования З. На Г. возложена обязанность в течение месяца со дня вступления решения суда в законную силу снести глухой забор (ограждение) возведенный по границе земельного участка. Отказывая в удовлетворении исковых требований в части возложения обязанности снести пристройку к жилому дому, суд первой инстанции исходил из того, что истцом не был доказан факт того, что пристройка ответчика представляет собой источник опасности для него, как смежного землепользователя. Открыть документ в вашей системе КонсультантПлюс:
Статья: «Дело о пасеке» как зеркало нищеты российского вещного права. Комментарий к Определению Судебной коллегии по гражданским делам ВС РФ от 28.05.2019 N 37-КГ19-4
(Латыев А.Н.)
(«Вестник экономического правосудия Российской Федерации», 2019, N 11)3.6. Как мы заметили, далеко не всегда существующие нормы соседского права являются императивными. Если оценивать их с содержательной точки зрения, то следует признать, что часть из таких норм направлена исключительно на защиту интересов соседа, а потому вполне могла бы изменяться соглашением заинтересованных лиц в их отношениях между собой (например, нормы о характеристиках забора или о расстоянии от границы участка до высаженных на соседнем участке деревьях, об организации стока с крыши дома соседа и т.п.), а часть — направлена на защиту интересов всех третьих или же любых оказавшихся рядом лиц. К числу последних можно с уверенностью отнести, скажем, противопожарные правила. Но даже они могут допускать некоторые вариации. Так, по общему правилу в целях защиты от пожара между строениями на соседних участках должны выдерживаться установленные расстояния, однако вполне можно представить себе возможность сокращения этих расстояний или же и вовсе строительства зданий без разрывов (вспомним тот самый знаменитый римский servitus oneris ferendi), но при условии разделения их брандмауэром. Таким образом, при допущении отступлений от нормативно определенных правил взаимодействия соседних земельных участков (а равно, наверное, и иных объектов недвижимости) модификации подлежат не только нормы гражданского права (причем, как мы видели, это нормы и вещного права, и обязательственного права, и — в какой-то мере — квазикорпоративного), но и нормы так называемого формального права, регламентирующего порядок и последствия регистрации прав , и сами нормы публичного права, на сегодняшний день выполняющие функции регулирования соседских отношений.

Нормативные акты: Расстояние от дома до забора Открыть документ в вашей системе КонсультантПлюс:
«Общие требования к садоводческим объединениям граждан»
(утв. МЧС России)Дом или другое жилое строение (а) должно находиться от красной линии (б) (это линия вашего забора) улиц на расстоянии не менее чем 5 метров, от красной линии проездов — не менее чем на 3 метра. Расстояние от хозяйственной постройки (с) до красной линии улиц и проездов должно быть не менее 5 метров.

Урок 26. расстояние от точки до прямой. расстояние между параллельными прямыми — Геометрия — 7 класс

Геометрия

7 класс

Урок № 26

Расстояние от точки до прямой. Расстояние между параллельными прямыми

Перечень рассматриваемых вопросов:

• Понятие наклонной.
• Расстояние от точки до прямой.
• Расстояние между параллельными прямыми.
• Теорема о равноудалённости точек параллельных прямых.

Тезаурус:

Наклонной, проведенной из данной точки к данной прямой, называется любой отрезок, соединяющий данную точку с точкой прямойине являющийся перпендикуляром к прямой.

Длина перпендикуляра, проведенного из точки к прямой, называется расстоянием от этой точки до прямой.

Все точки каждой из двух параллельных прямых равноудалены

от другой прямой.

Все точки плоскости, расположенные по одну сторону от данной прямой и равноудаленные от неё, лежат на прямой, параллельной данной.

Расстояние от произвольной точки одной из параллельных прямых до другой прямой называется расстоянием между этими прямыми.

Основная литература:

1. Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.

Дополнительная литература:

1. Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
2. Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
3. Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
4. Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
5. Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.

Теоретический материал для самостоятельного изучения.

Расстояние между двумя точками – длина отрезка, соединяющего эти точки. Введём также следующие понятия:

1) расстояние от точки до прямой;

2) расстояние между параллельными прямыми.

Пусть отрезок АН – перпендикуляр, проведённый из точки А к прямой а, М – любая точка прямой а, отличная от Н. Отрезок АМ называется наклонной, проведённой из точки А к прямой а. В прямоугольном треугольнике АНМ катет АН меньше гипотенузы АМ. Следовательно, перпендикуляр, проведённый из точки к прямой, меньше любой наклонной, проведённой из той же точки к этой прямой.

Длина перпендикуляра, проведённого из точки к прямой, называется расстоянием от этой точки до прямой.

Отметим, что расстояние от точки до прямой равно наименьшему из расстояний от этой точки до точек прямой.

На рисунке расстояние от точки В до прямой р равно 3 см, а расстояние от точки С до этой прямой равно 5 см.

Прежде чем ввести понятие расстояния между параллельными прямыми, рассмотрим одно из важнейших свойств параллельных прямых.

Теорема. Все точки каждой из двух параллельных прямых равноудалены от другой прямой.

Доказательство. Рассмотрим параллельные прямые а и b. Отметим на прямой a точку A и проведём из этой точки перпендикуляр AB к прямой b. Докажем, что расстояние от любой точки X прямой а до прямой b равно АВ.

Проведём из точки Х перпендикуляр XY к прямой b. Так как XY‎ перпендикулярно b, то XY‎ перпендикулярно а. Прямоугольные треугольники ABY и YXA равны по гипотенузе и острому углу (AY – общая гипотенуза, а углы 1 и 2 равны как накрест лежащие углы при пересечении параллельных прямых a и b секущей AY). Следовательно, XY = AB.

Итак, любая точка X прямой a находится на расстоянии AB от прямой b. Очевидно, что все точки прямой b находятся на таком же расстоянии от прямой a. Теорема доказана.

Из доказанной теоремы следует, что точка, движущаяся по одной из параллельных прямых, все время находится на одном и том же расстоянии от другой прямой.

Расстояние от произвольной точки одной из параллельных прямых до другой прямой называется расстоянием между этими прямыми.

Отметим, что расстояние между параллельными прямыми равно наименьшему из расстояний от точек одной прямой до точек другой прямой.

Замечание. Справедливо утверждение, обратное доказанной теореме: все точки плоскости, расположенные по одну сторону от данной прямой и равноудалённые от неё, лежат на прямой, параллельной данной.

Дано:
AA₁= BB₁= CC₁

Доказать: точкиA, B, C– принадлежатодной прямой, АА₁║ ВВ₁║СС_1.

Доказательство: по аксиоме параллельных прямых, через точку A проведем прямую b, b║a, тогда все точки b║a равноудаленыот точек прямой a. Докажем, что B, C∈ b.

Пусть B∉ b, C∉ b, значит, расстояние от точки B до a и C будет больше или меньше, чем расстояние h. Но это противоречит AA₁ = BB₁ = CC₁.

Следовательно, наше предположение неверно и A, B и С ∈ b || a, что и требовалось доказать.

Разбор заданий тренировочного модуля.

В равностороннем треугольнике ABC проведена биссектриса AD. Расстояние от точки D до прямой AC равно 12 см. Найти расстояние от точки A до прямой BC.

Объяснение: равносторонним треугольником называется треугольник с тремя равными сторонами (значит, и с тремя равными углами, то есть – по 60°). Равносторонний треугольник является частным случаем равнобедренного, поэтому все свойства, присущие равнобедренному треугольнику, распространяются и на равносторонний. Поэтому АD – не только биссектриса, но ещё и высота, стало быть AD⊥BC

Поскольку расстояние от точки D до прямой АС – это длина перпендикуляра, опущенного из точки D на прямую AC, то DH – данное расстояние. Рассмотрим треугольник AHD. В нём угол H = 90°, так как DH – перпендикуляр к AC (по определению расстояния от точки до прямой). Кроме этого, в данном треугольнике катет DH лежит против угла DAH = 30°, поэтому AD = 2 ∙ 12= 24см (по свойству).

Расстояние от точки А до прямой ВС – это длина опущенного на прямую ВС перпендикуляра. По доказанному AD⊥ BC, значит, AD = 24 см.

Ответ: 24 см.

Расстояние от точки до прямой. Расстояние между параллельными прямыми

Здравствуйте уважаемые ребята! 

Давайте начнем наше с вами путешествие к знаниям!

Сегодня мы поговорим о том, что называют расстоянием от какой-то заданной точки до прямой.  

В качестве практической ситуации рассмотрим схему.

Вы стоите в точке, которая на схеме обозначена цифрой 2. Дорога, на которую вам нужно попасть, чтобы поймать маршрутное такси до города, проходит в виде прямой через 1, 3  и 4. 

Вы рассматриваете три маршрута:

Первый — 21;

Второй — 23;

Третий — 24.

Вопрос: какой будет самый кротчайший путь?  Ведь вы очень спешите.
Наверное, вы заметили, что  кратчайшим расстоянием от данной точки 2, является путь 21. 
Данный путь он пересекает дорогу под прямым углом. Делаем вывод — ближайшим расстоянием между точкой и прямой — является перпендикуляр, опущенный из данной точки до этой прямой. Все остальные рассуждения, представленные ниже, только доказывают это.

Начнем наш урок. Открываем тетрадь. Записываем тему «

Расстояние от точки до прямой. Расстояние между параллельными прямыми».  страница в учебнике 81-83.

Изучим основные детали темы:

Видео YouTube

Определение:

Расстоянием между двумя точками А и В является длина отрезка АВ, соединяющего эти точки.

При этом следует отметить, что точки А и В можно соединить и таким образом:

Но именно кратчайший путь, то есть отрезок АВ, является расстоянием между данными точками.

Возьмём некоторую прямую b и точку А, которая не лежит на этой прямой. Опустим перпендикуляр из точки А к прямой b:

Полученный отрезок АН и будет называться расстоянием от точки А до прямой, так как это кратчайшее расстояние между данными точкой и прямой.

Действительно так. Отметим точку В на прямой b и рассмотрим прямоугольный треугольник АНВ:

АВ — гипотенуза, а АН — катет этого треугольника. Известно, что катет всегда меньше гипотенузы.

Отрезок АВ называется наклонной, проведённой из точки А к прямой b.

Перпендикуляр, проведённый из точки к прямой, меньше любой наклонной, проведённой из той же точки к этой прямой.,

Определение:

Длина перпендикуляра, проведённого из точки к прямой, называется расстоянием от этой точки до прямой.

Обозначают следующим образом:

. Так обозначают расстояние от точки А до прямой b. Читается буква как «ро».

Пусть а и b — параллельные прямые. Отметим на прямой а две точки А и В и опустим из них перпендикуляры АМ и BN на прямую b:

Если прямая a||b, а отрезки AM⊥b, BN⊥b, то АМ=BN и равняется расстоянию между параллельными прямыми а и b.

Проведём отрезок АN и рассмотрим полученные треугольники АBN и АМN:

Так как AM⊥b, а a||b, то AM⊥a. То есть ВN⊥b, а a||b, то и ВN⊥a.

Получили, что АBN и АМN — прямоугольные треугольники. У них сторона АN — общая, она является гипотенузой для обоих треугольников. Углы ВАN и АNМ равны, так как являются внутренними накрест лежащими при параллельных прямых АВ и MN и секущей АN.

Следовательно, получаем, что прямоугольные треугольники АBN и АМN равны по гипотенузе и острому углу. Из этого следует, что АМ=ВN.

Получили, что отрезки АМ и BN равны.

Расстоянием между параллельными прямыми является длина их общего перпендикуляра.

Обозначают следующим образом:

Верно и обратное утверждение:

Все точки плоскости, расположенные по одну сторону от прямой и находящиеся на равном расстоянии от неё, лежат на прямой параллельной данной.

Пример.

На рисунке отрезок АВ=6 см, ∠В=30 градусов. Найти расстояние от точки А до прямой а.

Опустим из точки А к прямой а перпендикуляр АС, который и есть расстояние от точки А до прямой а:

Получили прямоугольный треугольник АВС.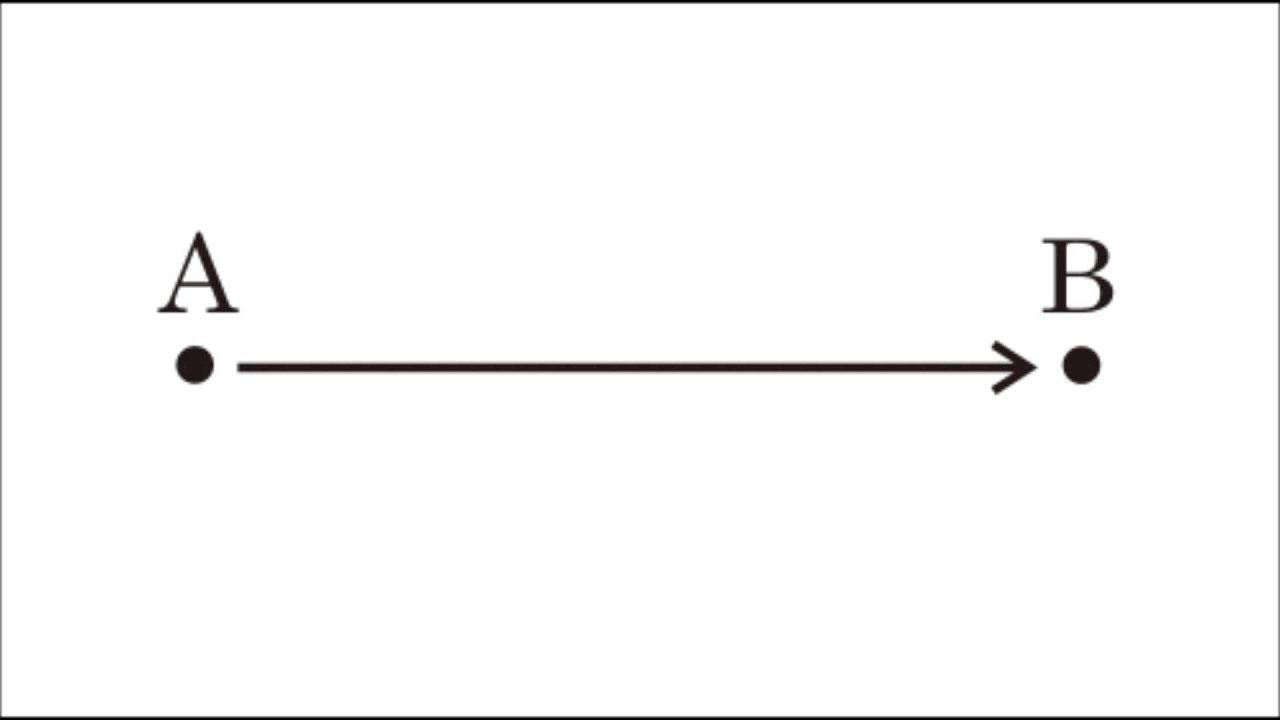 У которого ∠В=30 градусов, АВ=6см.

Известно, что катет прямоугольного треугольника, лежащий против угла в 30 градусов, равен половине гипотенузы. Получаем:

Пример.

На рисунке расстояние между параллельными прямыми а и b равно 5 сантиметров, а расстояние между параллельными прямыми а и с равно 9 сантиметров. Чему равно расстояние между параллельными прямыми b и с?

Известно, что:

Из этого следует:

Основные выводы по теме:

Домашняя работа.

Выполнить тест на двойном листочке, сделать фото решения и отправить его по почте  [email protected]

Требования: подписать листочек ФИО, дату домашнего задания. Сами задания оформить в сооответствии с требованиями оформления геометрической задачи: дано, найти, рисунок, решение, ответ.

Зонд НАСА «Паркер» побил рекорд скорости и близости к Солнцу

• Николай Воронин
• Корреспондент по вопросам науки и технологий

12 августа 2018

Обновлено 30 октября 2018

Для просмотра этого контента вам надо включить JavaScript или использовать другой браузер

Подпись к видео,

Прикоснуться к Солнцу — как это возможно?

Миссия НАСА, отправленная к Солнцу два с лишним месяца назад, приблизилась к нашей звезде на рекордно близкое расстояние — и продолжает движение.

Предыдущий рекорд принадлежал совместному американско-германскому спутнику «Гелиос-2»: в 1976 году тот приблизился к Солнцу на 42,73 млн км.

«Паркер», задача которого — «прикоснуться к Солнцу», пролетев сквозь солнечную корону, — должен подлететь к звезде примерно в семь раз ближе. В точке наибольшего приближения аппарат будет отделять от поверхности Солнца всего около 6 млн км — это в 25 раз ближе, чем орбита нашей планеты.

Попутно «Паркер» установил и новый рекорд скорости для объекта, когда-либо созданного руками человека: около 70 км/с.

Этот рекорд также продержался недолго: по мере приближения к Солнцу аппарат продолжает ускоряться, и, согласно расчетам, его пиковая скорость составит около 190 км/с (примерно 680 тысяч км/ч).

Близкий незнакомец

Несмотря на относительную близость — по космическим меркам, конечно, — мы не так уж и много знаем о нашей звезде.

Например, одна из главных загадок Солнца — почему внешняя часть атмосферы звезды в сотни раз горячее, чем поверхность звезды. Это всё равно как если бы нам становилось жарче по мере удаления от костра.

Невооружённым глазом с Земли мы можем наблюдать лишь ничтожную часть солнечного излучения, поэтому Солнце представляется нам очень спокойным и неизменным диском.

Автор фото, NASA

Подпись к фото,

Примерно так выглядит Солнце на самом деле

Автор фото, NASA

Подпись к фото,

Или так

На самом же деле его в самом прямом смысле непрерывно разрывают на части мощные взрывы, в результате чего потоки заряженных частиц и электромагнитного излучения — так называемый солнечный ветер — разлетаются на миллиарды километров вокруг.

Это открытие сделал в середине XX века американский астроном Юджин Паркер. Именно в его честь назван аппарат. 91-летний ученый был на месте запуска и попрощался с «Паркером».

На Земле порывы солнечного ветра вызывают северные сияния, магнитные бури и другие явления, известные под общим названием «космическая погода».

Подобные вспышки не только влияют на наше самочувствие, но и вносят помехи в радиосвязь, нарушают работу спутников, а иногда приводят к серьёзным сбоям в электросетях. В 1989 году, например, буря была настолько мощной, что солнечный ветер на несколько часов полностью обесточил канадскую провинцию Квебек, а северные сияния можно было наблюдать во Флориде и в Техасе, где обычно их не бывает.

Автор фото, NASA

Подпись к фото,

Так выглядит в первые секунды вспышка на Солнце, если снять её в разном световом диапазоне

«Наш мир постоянно омывается солнечной энергией, — объясняет один из руководителей проекта из Университета Джонса Хопкинса Ники Фокс. — Но у нас нет чёткого понимания, что за механизмы несут к нам солнечный ветер, и именно это мы собираемся выяснить».

Однако есть у миссии и совершенно практический смысл. Учёные надеются, что при помощи этого исследования они смогут лучше понять природу солнечного ветра — и, возможно, научиться предсказывать космическую погоду.

Например, в ближайшее время планируется отправить первых людей на Марс. Миссия продлится три с половиной года, и если за время полёта на Солнце произойдёт достаточно интенсивная вспышка, то все астронавты погибнут. На Земле от космического излучения нас защищает магнитосфера планеты, в открытом же космосе укрыться от солнечного ветра невозможно — его внезапный порыв может уничтожить электронику корабля и вызвать необратимые мутации в ДНК экипажа.

В самое пекло

«Паркер» должен ответить на несколько вопросов — в частности, почему ускоряется солнечный ветер, и как заряженным частицам удаётся достигать околосветовых скоростей. Для этого ему нужно будет максимально приблизиться к Солнцу, окунувшись в верхние слои атмосферы звезды.

По словам одной из руководителей миссии Николин Виалл, «у нас есть возможность засунуть градусник в самую корону (так называют внешние слои атмосферы Солнца — Би-би-си) и посмотреть, как поднимается температура».

Автор фото, University of Chicago

Подпись к фото,

Первооткрыватель солнечного ветра Юджин Паркер в Университете Чикаго

Но как «засунуть градусник» в Солнце так, чтобы он не расплавился?

От палящих лучей зонд укроет беспрецедентная термозащита: экран из многослойного углепластика толщиной около 12 см и сложная система из семи датчиков, задача которой — автономно, без сигнала с Земли, контролировать, чтобы аппарат всегда был повёрнут к Солнцу нужной, то есть защищенной, стороной.

Стоит «Паркеру» хотя бы частично высунуться за защитный экран — и аппарат, на создание и запуск которого потрачено 1,5 млрд долларов, рискует в лучшем случае выйти из строя, а в худшем — превратиться в сгусток плазмы.

Чтобы понять, как 12-сантиметровый экран может защитить от разрушительного жара звезды, нужно помнить о разнице между теплом и температурой. Температура измеряет, насколько быстро движутся частицы, а тепло — общее количество переносимой ими энергии. Частицы могут двигаться с невероятной скоростью (высокая температура), но если их количество невелико, то и передать много энергии они не смогут. Например, вы можете безболезненно ненадолго засунуть руку в разогретую духовку — но не в кипящую воду.

В открытом космосе — в условиях почти полного вакуума — частиц, способных разогреть аппарат, ничтожно мало. Верхние слои солнечной короны чрезвычайно разрежены, и хотя температура там достигает миллионов градусов, защитный экран «Паркера» нагреется только до 1300-1400 градусов.

При этом сам аппарат будет работать в весьма комфортных условиях около 30 градусов по Цельсию, а «хвост» трёхметрового зонда, отвёрнутый от Солнца, и вовсе будет погружён в настоящий космический холод — около 130 градусов ниже ноля. Заднюю часть «Паркера» даже придётся нагревать дополнительно, чтобы могла нормально работать расположенная там электроника.

17 лет ожидания

Владимир Красносельских — сотрудник французского Национального центра научных исследований, его команда отвечает за магнитные датчики одного из четырёх установленных на «Паркере» инструментов под названием FIELDS. Задача прибора — измерять электрические и магнитные поля вокруг аппарата.

Именно разработчикам FIELDS из Университета Беркли принадлежит идея «тараканьих усов» — тонких датчиков, вынесенных за пределы защитного экрана для более точного измерения разности потенциалов электрического поля. Сам Владимир сравнивает их с клеммами автомобильного аккумулятора.

Подпись к фото,

Владимир Красносельских ждал запуска 17 лет — но с еще большим нетерпением ждет первых результатов миссии

Владимир рассказывает, что изначально параллельно с «Паркером» планировалось запустить аналогичный зонд Европейского космического агентства. Аппараты должны были проводить измерения на расстоянии 10 и 60 радиусов от Солнца, но европейскую миссию пришлось отложить на 2020 год.

Работу над проектом FIELDS Владимир начал ещё в 2001 году — так что этого запуска НАСА он ждал 17 лет. Ученому особенно обидно, что стартовал «Паркер» только тогда, когда ему уже пора на пенсию и он уже не сможет набрать собственную команду для анализа собранной прибором информации.

«Запуск для нас не самое интересное, мы ждём первых данных, — говорит Красносельских. — Ведь до настоящего времени никто ничего подобного не делал. Уникальна не только сама миссия, но и наш эксперимент на ней».

При этом собранные на Солнце данные замеров аппарат сможет передать учёным, только когда вернётся к Земле — точнее, приблизится к ней на минимальное расстояние. А этот «тур» составляет 88 дней — ещё почти три месяца мучительного ожидания после запуска.

При этом пока никто точно не знает, какие именно результаты принесёт миссия — и когда им удастся найти практическое применение.

Владимир грустно шутит, что наука, которой он занимается, с одной стороны, недостаточно фундаментальная, чтобы получать за неё Нобелевские премии (её не удостоился даже сам Юджин Паркер, несмотря на все свои открытия), а с другой — недостаточно прикладная, чтобы на неё охотно выделяли деньги.

«Нам постоянно приходится убеждать людей в том, что то, чем мы занимаемся, действительно нужно, — улыбается Красносельских. — Но давайте дождёмся очередной интенсивной вспышки на Солнце — и тогда все скажут: какую же полезную работу делали эти учёные!»

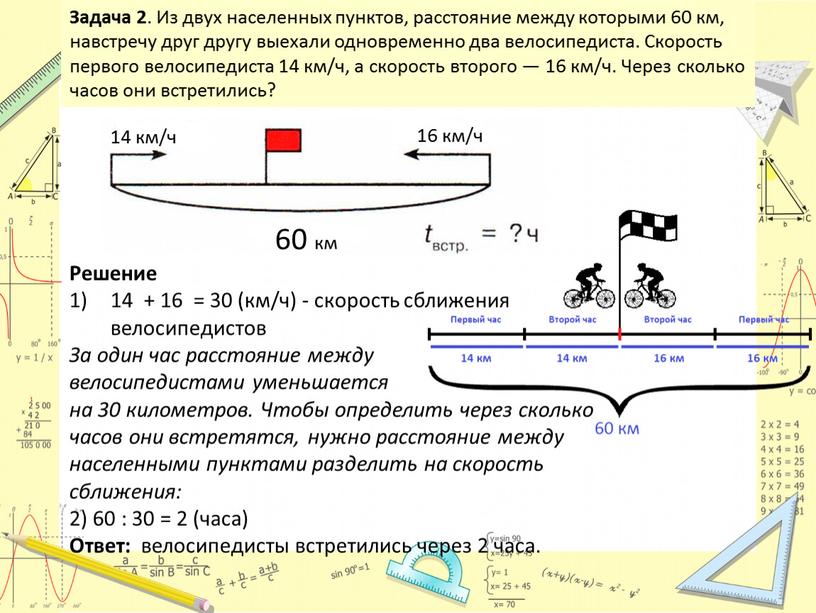
Текстовые задачи. Задачи на движение с решениями

Задачи на движение с решениями

перейти к содержанию курса текстовых задач

1. Первый турист проехал 2 ч на велосипеде со скоростью 16 км/ч. Отдохнув 2 ч, он отравился дальше с прежней скоростью. Спустя 4 ч после старта велосипедиста ему вдогонку выехал второй турист на мотоцикле со скоростью 56 км/ч. На каком расстоянии от места старта мотоциклист догонит велосипедиста? Решение
2. Из пункта A в пункт B отправились три машины друг за другом с интервалом в 1 ч. Скорость первой машины равна 50 км/ч, а второй — 60 км/ч. Найти скорость третьей машины, если известно, что она догнала первые две машины одновременно. Решение
3. Поезд был задержан в пути на 12 мин, а затем на расстоянии 60 км наверстал потерянное время, увеличив скорость на 15 км/ч. Найти первоначальную скорость поезда. Решение
4. Расстояние между станциями A и B равно 103 км. Из A в B вышел поезд и, пройдя некоторое расстояние, был задержан, а потому оставшийся до B путь проходил со скоростью, на 4 км/ч большей, чем прежняя. Найти первоначальную скорость поезда, если известно, что оставшийся до B путь был на 23 км длиннее пути, пройденного до задержки, и что на прохождение пути после задержки было затрачено на 15 мин больше, чем на прохождение пути до нее. Решение
5. Скорость автомобиля по ровному участку на 5 км/ч меньше, чем скорость под гору, и на 15 км/ч больше, чем скорость в гору. Дорога из A в B идет в гору и равна 100 км. Определить скорость автомобиля по ровному участку, если расстояние от A до B и обратно он проехал за 1 ч 50 мин. Решение
6. Автобус проходит расстояние между пунктами A и B по расписанию за 5 ч. Однажды, выйдя из A, автобус был задержан на 10 мин в 56 км от A и, чтобы прибыть в B по расписанию, он должен был оставшуюся большую часть пути двигаться со скоростью, превышающей первоначальную на 2 км/ч. Найти скорость движения автобуса по расписанию и расстояние между пунктами A и B, если известно, что это расстояние превышает 100 км. Решение
7. Поезд проходит мимо платформы за 32 с. За сколько секунд поезд проедет мимо неподвижного наблюдателя, если длина поезда равна длине платформы? Решение
8. Два поезда отправляются навстречу друг другу с постоянными скоростями, один из А в В, другой из В в А. Они могут встретиться на середине пути, если поезд из А отправится на 1,5 ч раньше. Если бы оба поезда вышли одновременно, то через 6 ч расстояние между ними составило бы десятую часть первоначального. Сколько часов каждый поезд тратит на прохождение пути между А и В? Решение
9. От пристани А одновременно отправились вниз по течению катер и плот. Катер спустился вниз на 96 км, потом повернул обратно и вернулся в А через 14 ч. Найти скорость катера в стоячей воде и скорость течения, если известно, что катер встретил плот на обратном пути расстоянии 24 км от А. Решение
10. Пункт В находится по реке ниже пункта А. В одно и то же время из пункта А отплыли плот и первая моторная лодка, а из пункта В — вторая моторная лодка. Через некоторое время лодки встретились в пункте С, а плот за это время проплыл третью часть пути от А до С. Если бы первая лодка без остановки доплыла до пункта В, то плот за это время прибыл бы в пункт С. Если бы из пункта А в пункт В отплыла вторая лодка, а из пункта В в пункт А — первая лодка, то они встретились бы в 40 км от пункта А. Какова скорость обеих лодок в стоячей воде, а также расстояние между пунктами А и В, если скорость течения реки равна 3 км/ч? Решение
11. Два тела, двигаясь по окружности в одном направлении, встречаются через каждые 112 мин, а двигаясь в противоположных направлениях — через каждые 16 мин. Во втором случае расстояние между телами уменьшилось с 40 м до 26 м за 12 с. Сколько метров в минуту проходит каждое тело и какова длина окружности? Решение
12. Две точки, двигаясь по окружности в одном направлении, встречаются каждые 12 мин, причем первая обходит окружность на 10 с быстрее, чем вторая. Какую часть окружности проходит за 1 с каждая точка? Решение
13. Два тела движутся навстречу друг другу из двух точек, расстояние между которыми 390 м. Первое тело прошло в первую секунду 6 м, а в каждую последующую секунду проходило на 6 м больше, чем в предыдущую. Второе тело двигалось равномерно со скоростью 12 м/c и начало движение спустя 5 с после первого. Через сколько секунд после того, как начало двигаться первое тело, они встретятся? Решение

Задачи для самостоятельного решения

1. Дорога от A до D длиной в 23 км идет сначала в гору, затем — по ровному участку, а потом — под гору. Пешеход, двигаясь из A в D, прошел весь путь за 5 ч 48 мин, а обратно, из D в A, — за 6 ч 12 мин. Скорость его движения в гору равна 3 км/ч, по ровному участку — 4 км/ч, а под гору — 5 км/ч. Определить длину дороги по ровному участку. Ответ:  8 км
2. В 5 ч утра со станции A вышел почтовый поезд по направлению к станции B, отстоящей от A на 1080 км. В 8 ч утра со станции B по направлению к A вышел пассажирский поезд, который проходил в час на 15 км больше, чем почтовый. Когда встретились поезда, если их встреча произошла в середине пути AB? Ответ: в 5 ч дня
3. Из пункта A впунктB отправились три велосипедиста. Первый из них ехал со скоростью 12 км/ч. Второй отправился на 0,5 ч позже первого и ехал со скоростью 10 км/ч. Какова скорость третьего велосипедиста, который отправился на 0,5 ч позже второго, если известно, что он догнал первого через 3 ч после того как догнал второго? Ответ: 15 км/ч
4. Два поезда — товарный длиной в 490 м и пассажирский длиной в 210 м — двигались навстречу друг другу по двум параллельным путям. Машинист пассажирского поезда заметил товарный поезд, когда он находился от него на расстоянии 700 м; через 28 с после этого поезда встретились. Определить скорость каждого поезда, если известно, что товарный поезд проходит мимо светофора на 35 с медленнее пассажирского. Ответ:  36 км/ч; 54 км/ч
5. Турист A и турист B должны были выйти одновременно навстречу друг другу из поселка M ипоселкаN соответственно. Однако турист A задержался и вышел позже на 6 ч. При встрече выяснилось, что A прошел на 12 км меньше, чем B. Отдохнув, туристы одновременно покинули место встречи и продолжили путь с прежней скоростью. В результате A пришел в поселок N через 8 ч, а B пришел в поселок M через 9 ч после встречи. Определить расстояние MN и скорости туристов. Ответ:  84 км; 6 км/ч; 4 км/ч.
6. Пешеход, велосипедист и мотоциклист движутся по шоссе в одну сторону с постоянными скоростями. В тот момент, когда пешеход и велосипедист находились в одной точке, мотоциклист был на расстоянии 6 км позади них, а тот момент, когда мотоциклист догнал велосипедиста, пешеход отстал от них на 3 км. На сколько километров велосипедист обогнал пешехода в тот момент, когда пешехода настиг мотоциклист? Ответ: 2 км
7. Два туриста вышли одновременно из пункта A в пункт B.Первый турист проходил каждый километр на 5 мин быстрее второго. Пройдя 20% расстояния от A до B, первый турист повернул обратно, пришел в A, пробыл там 10 мин, снова пошел в B и оказался там одновремен-
   но со вторым туристом. Определить расстояние от A до B, если второй турист прошел его за 2,5 ч. Ответ: 10 км
8. Рыбак проплыл на лодке от пристани против течения 5 км и возвратился обратно на пристань. Скорость течения реки равна 2,4 км/ч. Если бы рыбак греб с той же силой в неподвижной воде озера на лодке с парусом, увеличивающим скорость на 3 км/ч, то он за то же время проплыл бы 14 км. Найти скорость лодки в неподвижной воде. Ответ:  9,6 км/ч
9. Моторная лодка проплыла по озеру, а потом спустилась вниз по реке, вытекающей из озера. Расстояние, пройденное лодкой по озеру, на 15% меньше расстояния, пройденного по реке. Время движения лодки по озеру на 2% больше, чем по реке. На сколько процентов скорость движения лодки вниз по реке больше скорости движения по озеру? Ответ: на 20%
10. Турист проплыл в лодке по реке из города A в город B и обратно, затратив на это 10 ч. Расстояние между городами равно 20 км. Найти скорость течения реки, зная, что турист проплывал 2 км против течения реки за такое же время, как 3 км по течению. Ответ: 5/6 км/ч
11. По окружности длиной 60 м равномерно в одном направлении движутся две точки. Одна из них совершает полный оборот на 5 с быстрее другой. При этом совпадение точек происходит каждый раз через 1 мин. Определить скорости точек. Ответ:  4 м/с; 3 м/с.
12. Из точек A и B одновременно начали двигаться два тела навстречу друг другу. Первое в первую минуту прошло 1 м, а в каждую последующую проходило на 0,5 м больше, чем в предыдущую. Второе тело проходило каждую минуту по 6 м. Через сколько минут оба тела встретились, если расстояние между A и B равно 117 м? Ответ: через 12 мин.
13. Два приятеля в одной лодке прокатились по реке вдоль берега и вернулись по одной и той же речной трассе через 5 ч с момента отплытия. Протяженность всего рейса составила 10 км. По их подсчетам получилось, что на каждые 2 км против течения в среднем потребовалось столько же времени, сколько на каждые 3 км по течению. Найти скорость течения реки, а также время проезда туда и время проезда обратно. Ответ:  5/12 км/ч; 2 ч и 3 ч.

 

Метки движение, текстовые задачи. Смотреть запись.

Графическое определение расстояния от точки до прямой

Расстояние от точки до прямой – это длина перпендикуляра, опущенного из точки на прямую. В начертательной геометрии она определяется графическим путем по приведенному ниже алгоритму.

Алгоритм

1. Прямую переводят в положение, в котором она будет параллельна какой-либо плоскости проекции. Для этого применяют методы преобразования ортогональных проекций.
2. Из точки проводят перпендикуляр к прямой. В основе данного построения лежит теорема о проецировании прямого угла.
3. Длина перпендикуляра определяется путем преобразования его проекций или с использованием способа прямоугольного треугольника.

Пример

На следующем рисунке представлен комплексный чертеж точки M и прямой b, заданной отрезком CD. Требуется найти расстояние между ними.

Решение

Согласно нашему алгоритму, первое, что необходимо сделать, это перевести прямую в положение, параллельное плоскости проекции. При этом важно понимать, что после проведенных преобразований фактическое расстояние между точкой и прямой не должно измениться. Именно поэтому здесь удобно использовать метод замены плоскостей, который не предполагает перемещение фигур в пространстве.

Результаты первого этапа построений показаны ниже. На рисунке видно, как параллельно b введена дополнительная фронтальная плоскость П₄. В новой системе (П₁, П₄) точки C»₁, D»₁, M»₁ находятся на том же удалении от оси X₁, что и C», D», M» от оси X.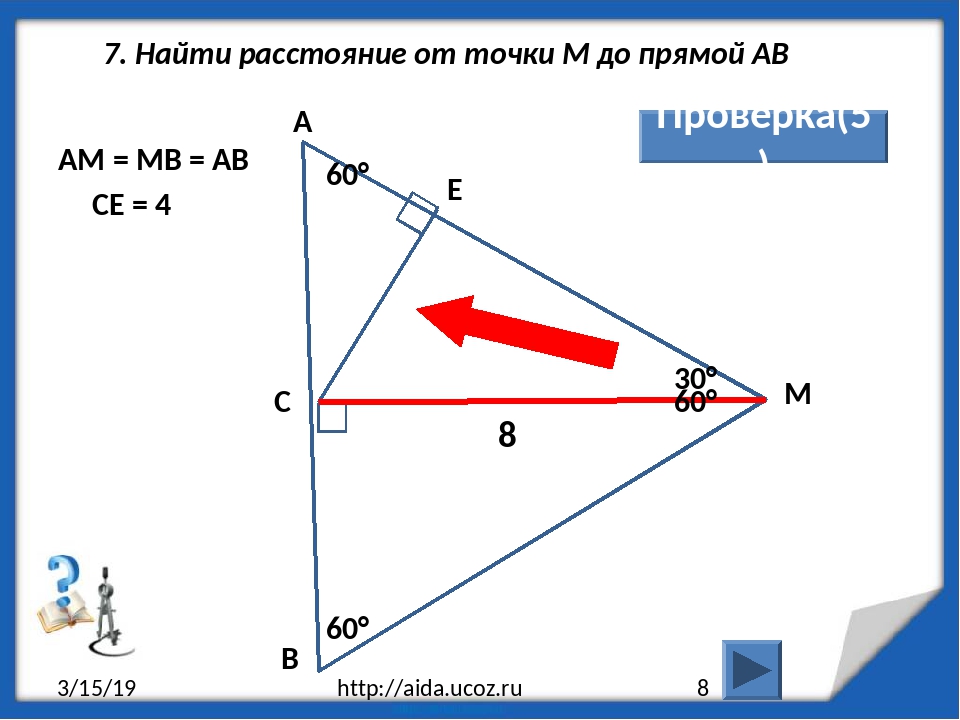

Выполняя вторую часть алгоритма, из M»₁ опускаем перпендикуляр M»₁N»₁ на прямую b»₁, поскольку прямой угол MND между b и MN проецируется на плоскость П₄ в натуральную величину. По линии связи определяем положение точки N’ и проводим проекцию M’N’ отрезка MN.

На заключительном этапе нужно определить величину отрезка MN по его проекциям M’N’ и M»₁N»₁. Для этого строим прямоугольный треугольник M»₁N»₁N₀, у которого катет N»₁N₀ равен разности (Y_M1 – Y_N1) удаления точек M’ и N’ от оси X₁. Длина гипотенузы M»₁N₀ треугольника M»₁N»₁N₀ соответствует искомому расстоянию от M до b.

Второй способ решения

• Параллельно CD вводим новую фронтальную плоскость П₄. Она пересекает П₁ по оси X₁, причем X₁∥C’D’. В соответствии с методом замены плоскостей определяем проекции точек C»₁, D»₁ и M»₁, как это изображено на рисунке.
• Перпендикулярно C»₁D»₁ строим дополнительную горизонтальную плоскость П₅, на которую прямая b проецируется в точку C’₂ = b’₂.
• Величина расстояния между точкой M и прямой b определяется длиной отрезка M’₂C’₂, обозначенного красным цветом.

Похожие задачи:

Модуль числа, определение и свойства

Определение модуля числа

Алгебра дает четкое определения модуля числа. Модуль в математике — это расстояние от начала отсчёта до точки координатной прямой, соответствующей этому числу.

Если мы возьмем некоторое число «a» и изобразим его на координатной прямой точкой «A» — расстояние от точки «A» до начала отсчёта (то есть до нуля, длина отрезка «OA») будет называться модулем числа «a».

Знак модуля: |a| = OA

Разберем на примере:

Точка «В», которая соответствует числу «−3», находится на расстоянии 3 единичных отрезков от точки 0 (то есть от начала отсчёта). То есть длина отрезка «OB» равна 3 единицам.

Число 3 (длина отрезка «OB») называют модулем числа «−3».

Обозначение модуля: |−3| = 3

Читают символы выше следующим образом: «модуль числа минус три равен трем».

Точка «С», которая соответствует числу «+4», находится на расстоянии четырех единичных отрезков от начала отсчёта, то есть длина отрезка «OС» равна четырем единицам.

Число 4 называют модулем числа «+4» и обозначают так: |+4| = 4.

Также можно опустить плюс и записать значение, как |4| = 4.

Свойства модуля числа

Давайте рассмотрим семь основных свойств модуля. Независимо от того, в какой класс перешел ребенок — эти правила пригодятся всегда.

1. Модуль числа — это расстояние, а расстояние не может быть отрицательным. Поэтому и модуль числа не бывает отрицательным:

2. Модуль положительного числа равен самому числу.

3. Модуль отрицательного числа равен противоположному числу.

• |−a| = a, если a < 0

4. Модуль нуля равен нулю.

5. Противоположные числа имеют равные модули.

6. Модуль произведения равен произведению модулей этих чисел.

• |a b| = |a| |b|, когда

a·b 0

или

−(a·b), когда a·b<0

7. Модуль частного равен частному от деления модуля числа числителя на модуль числа знаменателя: 

Геометрическая интерпретация модуля

Как мы уже знаем, модуль числа — это расстояние от нуля до данного числа. То есть расстояние от точки −5 до нуля равно 5.

Нарисуем числовую прямую и отобразим это на ней.

Эта геометрическая интерпретация используется для решения уравнений и неравенств с модулем. Давайте рассмотрим на примерах.

Решим уравнение: |х| = 5

Мы видим, что на числовой прямой есть две точки, расстояние от которых до нуля равно 5. Это точки 5 и −5. Значит, уравнение имеет два решения: x = 5 и x = −5.

Когда у нас есть два числа a и b, то их разность |a — b| равна расстоянию между ними на числовой прямой. Или длине отрезка АВ

Расстояние от точки a до точки b равно расстоянию от точки b до точки a, тогда |a — b| = |b — a|.

Решим уравнение: |a — 3| = 4 . Запись читаем так: расстояние от точки а до точки 3 равно 4. Отметим на числовой прямой точки, удовлетворяющие этому условию.

Уравнение имеет два решения: −1 и 7. Мы из 3 вычли 4 — и это один ответ, а также к 3 мы прибавили 4 — и это второй ответ.

Решим неравенство: |a + 7| < 4 .

Эту запись читаем так: расстояние от точки a до точки −7 меньше четырёх. Отмечаем на числовой прямой точки, удовлетворяющие этому условию:

Ответ в данном случае будет таким: (-11; -3).

Решим неравенство: |10 − x| ≥ 7.

Расстояние от точки 10 до точки x больше или равно семи. Отметим эти точки на числовой прямой.

Ответ: ( -; 3] [17, +)

График функции

График функции равен y = |х|.

Для x 0 имеем y = x. 

Для x < 0 имеем y = −x. В результате получаем:

Этот график можно использовать при решении уравнений и неравенств.

Корень из квадрата

В контрольной или задаче ЕГЭ может встретиться задачка, в которой просят вычислить √a² , где a – некоторое число или выражение.

При этом, √a²= |a|.

По определению арифметического квадратного корня √a² — это такое неотрицательное число, квадрат которого равен a² . 

Оно равно a, при а 0 и -а, при а < 0 , т. е. как раз |a|.

Модуль комплексного числа

У нас есть комплексное число, которое выглядит следующим образом: z=x+i·y, где x и y представляют собой действительную и мнимую части комплексного числа z (и являются действительными), а i — мнимая единица и равна √-1

Чему равен модуль числа в данном случае? Это арифметический квадратный корень из суммы квадратов действительной и мнимой части комплексного числа:

Свойства модуля комплексных чисел Область определения: вся комплексная плоскость. Область значений: [0;+∞). Модуль как комплексная функция не дифференцируется ни в одной точке, так как условия Коши-Римана не выполнены.

Модуль рационального числа

Как найти модуль рационального числа — это расстояние от начала отсчёта до точки координатной прямой, которая соответствует этому числу.

Модуль рационального числа, примеры:

|-3,5| = 3,5

|0| = 0

Модуль вещественных чисел

• Область определения: (−∞;+∞).
• Область значений: [0;+∞).
• Функция чётная.
• Функция дифференцируется везде, кроме нуля. В точке x=0 функция претерпевает излом.

Модуль противоположного числа, нуля, отрицательного и положительного чисел

Исходя из свойств модуля, которые мы рассмотрели выше, получаем:

• Противоположные числа имеют равные модули, то есть |- а| = |а| = a.
  Если посмотреть это относительно координатной прямой, то две точки, у которых координаты — это противоположные числа, располагаются на одном расстоянии от начала отсчета. То есть модули противоположных чисел одинаковы.
• Модуль нуля равен нулю.
  |0| = 0, если a = 0
• Для положительного числа модуль равен самомý числу, а для отрицательного – противоположному числу.
  |а| = — а
  |−a| = a

Приходите заниматься нескучной математикой в детскую онлайн-школу Skysmart. Поможем ребенку разобраться в сложной теме, подготовиться к контрольной, подтянуть оценки и чувствовать себя увереннее на математике в школе.

Запишите вашего ребенка на бесплатный пробный урок и начните заниматься уже завтра.

Формула расстояния

Вы знаете, что расстояние А B между двумя точками на плоскости с Декартово координаты А ( Икс 1 , y 1 ) и B ( Икс 2 , y 2 ) дается следующей формулой:

А B знак равно ( Икс 2 — Икс 1 ) 2 + ( y 2 — y 1 ) 2

Формула расстояния на самом деле просто Теорема Пифагора в маскировке.

Чтобы рассчитать расстояние А B между точкой А ( Икс 1 , y 1 ) и B ( Икс 2 , y 2 ) сначала нарисуйте прямоугольный треугольник с отрезком А B ¯ как его гипотенуза.

Если длины сторон равны а и б , то по теореме Пифагора

( А B ) 2 знак равно ( А C ) 2 + ( B C ) 2

Решение на расстоянии А B , у нас есть:

А B знак равно ( А C ) 2 + ( B C ) 2

С А C горизонтальное расстояние, это просто разница между Икс -координаты: | ( Икс 2 — Икс 1 ) | .Так же, B C это вертикальное расстояние | ( y 2 — y 1 ) | .

Поскольку мы все равно возводим эти расстояния в квадрат (а квадраты всегда неотрицательны), нам не нужно беспокоиться об этих знаках абсолютного значения.

А B знак равно ( Икс 2 — Икс 1 ) 2 + ( y 2 — y 1 ) 2

Пример:

Найдите расстояние между точками А и B на рисунке выше.

В приведенном выше примере у нас есть:

А ( Икс 1 , y 1 ) знак равно ( — 1 , 0 ) , B ( Икс 2 , y 2 ) знак равно ( 2 , 7 )

так

А B знак равно ( 2 — ( — 1 ) ) 2 + ( 7 — 0 ) 2 знак равно 3 2 + 7 2 знак равно 9 + 49 знак равно 58

или примерно 7.6 единицы измерения.

Формула расстояния

| Рассчитайте расстояние между 2 точками

В этом видео мы рассмотрим формулу расстояния. Формула расстояния используется для нахождения расстояния между двумя точками, в данном случае расстояние от A до B . В видеоуроке выше будет рассмотрен пример формулы средней точки и показано, как формула средней точки связана с теоремой Пифагора. После того, как вы закончите этот урок, просмотрите все наши уроки предварительной алгебры и практические задачи.

Что такое формула расстояния?

Формула расстояния:

Например:
Если точка A была (1,2), а точка B была (4,6), то мы должны найти расстояние между двумя точками.

Если вы не хотите запоминать формулу, то есть другой способ найти расстояние между двумя точками. Нарисуйте линию от нижней точки параллельно оси x, а линию от верхней точки параллельно оси y, тогда будет сформирован прямоугольный треугольник.Затем мы можем использовать теорему Пифагора для определения расстояния.

Расстояние одной ноги — это разница в крестиках. 4-1 = 3, так что сторона треугольника равна 3. Расстояние до другого отрезка — это разница в y. 6-2 = 4, так что сторона треугольника равна 4. Теперь мы можем использовать теорему Пифагора. Формула расстояния фактически основана на этом:

Если мы решили с помощью теоремы Пифагора, то:

Расстояние от точки A до точки B определяется с помощью формулы расстояния и теоремы Пифагора.

Примеры формулы расстояния

Пример 1

Найдите расстояние между двумя точками и

Формула расстояния:

Замените данное, затем оцените

Теперь у нас

Пример 2

Какое расстояние между точками (4, 3) и (-4, -3)?

Формула расстояния:

Замените данное, затем оцените

Теперь у нас

Стенограмма видеоурока

В этом уроке давайте обсудим формулу расстояния.

Формула расстояния используется для определения расстояния между двумя точками.

В данном случае расстояние от точки до точки.

У нас есть координаты точки.

И точка имеет координаты.

Формула расстояния

Вы можете запомнить эту формулу и найти расстояние между любыми двумя точками.

Приведем пример.

Точка имеет координаты. Точка имеет координаты. Давайте найдем расстояние между этими двумя точками.

Формула расстояния

Теперь у нас

Это означает, что расстояние между точкой и точкой равно.

Если вы не хотите запоминать формулу, есть другой способ найти расстояние между двумя точками.

Это очень похоже на формулу.

Нарисуем треугольник, проведя линию от до точки.

Обязательно сделайте треугольник с углом.

Тогда мы можем использовать теорему Пифагора.

Расстояние горизонтального отрезка — это разность двух координат. Давай назовем это.

Тогда расстояние до вертикального отрезка — это разность двух координат. Назовем эту ногу.

Теперь взглянем на теорему Пифагора.

Формула расстояния фактически основана на этом.

Итак, давайте решим это с помощью теоремы Пифагора

Тогда давайте возьмем квадратный корень, чтобы получить ответ.

Итак, мы получили тот же ответ, что и первый.

Итак, теперь вы можете запомнить формулу расстояния или нарисовать треугольник и использовать теорему Пифагора.

Расстояние между двумя точками: определение, формулы и примеры

Мы в Cuemath считаем, что математика — это жизненный навык. Наши эксперты по математике сосредотачиваются на том, «почему» стоит за «что». Учащиеся могут исследовать огромное количество интерактивных листов, наглядных пособий, симуляторов, практических тестов и многого другого, чтобы глубже понять концепцию.

Забронируйте БЕСПЛАТНОЕ пробное занятие сегодня! и поучаствуйте в онлайн-классе Cuemath LIVE вместе со своим ребенком.

Определение расстояния между двумя точками

Расстояние между любыми двумя точками — это длина отрезка линии, соединяющего точки.

Например, если \ (A \) и \ (B \) — две точки, и если \ (\ overline {AB} = 10 \) см, это означает, что расстояние между \ (A \) и \ (B \ ) составляет \ (10 ​​\) см.

Расстояние между двумя точками — это длина соединяющего их отрезка (но НЕ МОЖЕТ быть длиной соединяющей их кривой).2} \]

Это называется формулой расстояния .

Давайте теперь узнаем, как вывести эту формулу.

---

Формула доказательства расстояния

Допустим, что:

\ [A = (x_1, y_1) \\ [0,2 см] B = (x_2, y_2) \]

Далее предположим, что \ (\ overline {AB} = d \)

Теперь мы нанесем данные точки на координатную плоскость и соединим их линией.

Далее мы построим прямоугольный треугольник с гипотенузой \ (\ overline {AB} \).2} \]

Расстояние до точки \ ((a, b) \) от:

(i) ось x равна \ (| b | \)

(ii) ось y равна \ (| a | \)

Здесь , мы использовали знаки абсолютного значения, потому что расстояние никогда не может быть отрицательным.

Помогите своему ребенку набрать больше баллов с помощью запатентованного БЕСПЛАТНОГО диагностического теста Cuemath. Получите доступ к подробным отчетам, индивидуальным планам обучения и БЕСПЛАТНОЙ консультации. Попытайтесь проверить сейчас.

---

Решенные примеры

Найдите расстояние между двумя точками \ ((2, -6 \)) и \ ((7, 3 \))

Решение:

Предположим, что данные точки равны:

\ [\ begin {align} (x_1, y_1) & = (2, -6) \\ [0.2} \\ [0,3 см] d & = \ sqrt {25 + 81} \\ [0,3 см] d & = \ sqrt {106} \ end {align} \]

\ (\ следовательно \) Расстояние \ (= \ sqrt {106} \)

Покажите, что точки \ ((2, -1), (0, 1) \) и \ ((2, 3 \)) являются вершинами прямоугольного треугольника.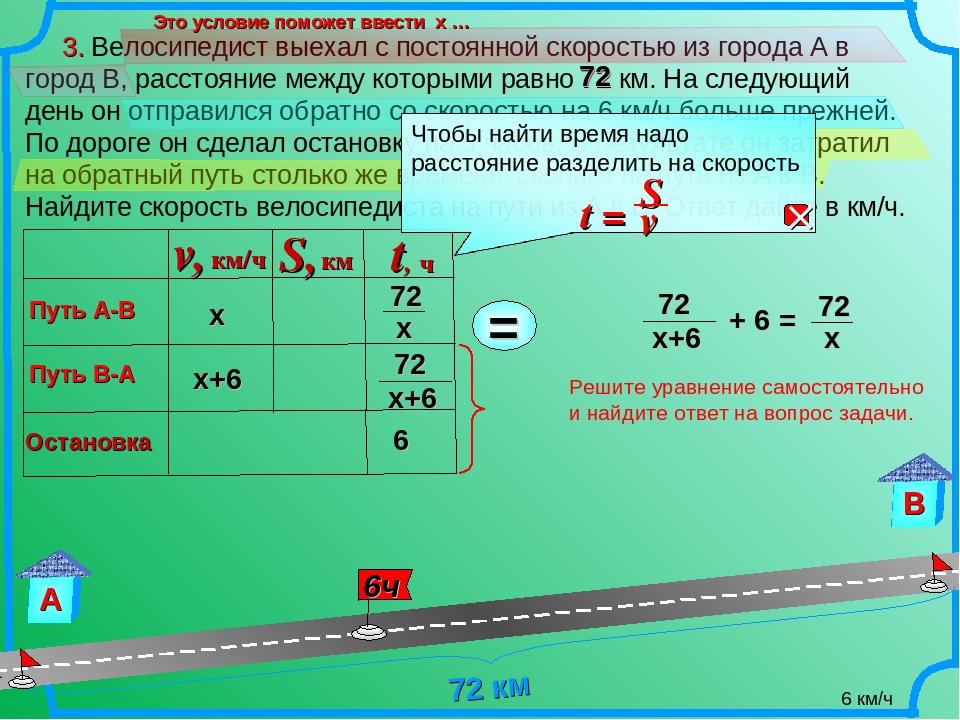

Решение:

Предположим, что данные точки равны:

\ [\ begin {align} A & = (2, -1) \\ [0,2 см] B & = (0,1) \\ [0.2 \\ [0,3 см] 8 + 8 & = 16 \\ [0,3 см] 16 & = 16 \ конец {выровнено} \]

Таким образом, \ (A, B \) и \ (C \) удовлетворяют теореме Пифагора.

Итак, \ (\ треугольник ABC \) прямоугольный треугольник.

Мы можем доказать то же самое, отметив все координаты на графике:

Таким образом,

Данные точки образуют прямоугольный треугольник.

Найдите точку на оси Y, которая равноудалена от точек \ ((- 1, 2 \)) и \ ((2, 3) \)

Решение:

Мы знаем, что координата x любой точки на оси y равна \ (0 \)

Следовательно, мы считаем точку, равноудаленную от данных точек, равной \ ((0, k \)).2-6k \\ 2k & = 8 \\ k & = 4 \ end {align} \]

Следовательно, требуемая точка \ ((0, k) = (0, 4) \)

\ (\ следовательно \) Обязательная точка \ (= (0, 4) \)

---

Калькулятор расстояния между двумя точками

Вот «Калькулятор расстояния между двумя точками».

Здесь вы можете ввести координаты двух точек, и он покажет вам расстояние между ними с пошаговым объяснением.

CLUEless по математике? Узнайте, как CUEMATH Учителя объяснят Расстояние между двумя точками вашему ребенку, используя интерактивные симуляции и рабочие листы, чтобы им больше никогда не приходилось запоминать что-либо по математике!

Изучите интерактивные и персонализированные онлайн-классы Cuemath, которые сделают вашего ребенка экспертом по математике. Забронируйте БЕСПЛАТНОЕ пробное занятие сегодня!

---

Практические вопросы

Сложные вопросы

1. Вершинами прямоугольника являются \ ((- 4, -3), (4, -3), (4, 3), \) и \ ((- 4, 3) \). 2} \]

   Это называется формулой расстояния .

   Упражнения по математике

   ]]> Матрицы Алгебра Геометрия Функции Тригонометрия Координатная геометрия Комбинаторика Сумма и ресторан Продукт на эскаларе Продукт Inversa Мономы Полиномы Особые продукты Уравнения Квадратные уравнения Радикальные выражения Системы уравнений Последовательности и серии Внутренний продукт Экспоненциальные уравнения Матрицы Детерминанты Инверсия матрицы Логарифмические уравнения Системы трех переменных уравнений Двумерные фигуры Площади Теорема Пифагора Расстояния Графики Определение уклона Положительный или отрицательный наклон Определить наклон прямой Ecuación de una recta Уравнение прямой (из графика) Квадратичная функция Posición relativa de dos rectas Асимптоты Пределы Distancias Непрерывность и разрывы Теорема Пифагора Синус Косинус Касательная Косеканс Секант Котангенс Тригонометрические идентичности Тригонометрические функции острого угла Тригонометрические функции связанных углов Решение прямоугольных треугольников Закон косинусов Закон синусов Ecuación de una recta Posición relativa de dos rectas Distancias Углы в пространстве Внутренний продукт Факториал Вариации без повторов Вариации с повторением Перестановки с повторением Перестановки без повторов Упражнения Круговые перестановки Биномиальный коэффициент Комбинации с повторением Комбинации без повторов Среднее арифметическое

   Формула расстояния | Блестящая вики по математике и науке

   Предположим, что A = x1A = x_1A = x1 и B = x2B = x_2B = x2 — две точки, лежащие на прямой действительных чисел. Тогда расстояние между AAA и BBB равно

   d (A, B) = ∣x1 − x2∣. d (A, B) = \ lvert x_1 — x_2 \ rvert. d (A, B) = ∣x1 — x2 ∣.

   На плоскости мы можем рассматривать ось xxx как одномерную числовую линию, поэтому мы можем вычислить расстояние между любыми двумя точками, лежащими на оси xxx, как абсолютное значение разности их xxx-координат. Точно так же расстояние между любыми двумя точками, лежащими на оси yyy, является абсолютной величиной разницы их yyy-координат.2} .d (P1, P2) = (x1 — x2) 2+ (y1 — y2) 2.

   Поскольку ∣x1 − x2∣ \ lvert x_1 — x_2 \ rvert∣x1 −x2 ∣ — это расстояние между xxx-координатами двух точек и ∣y1 − y2∣ \ lvert y_1 — y_2 \ rvert∣y1 — y2 ∣ — расстояние между yyy-координатами двух точек, формулу расстояния в плоскости xyxyxy можно представить как длину гипотенузы прямоугольного треугольника с вершинами P1 = (x1, y1) P_1 = ( x_1, y_1) P1 = (x1, y1), P2 = (x2, y2), P_2 = (x_2, y_2), P2 = (x2, y2) и P = (x2, y1) P = (x_2, y_1) P = (x2, y1).Тогда формула расстояния — это просто утверждение теоремы Пифагора.

   И в 1D, и в 2D функция расстояния удовлетворяет следующим свойствам:

   1. d (P, Q) ≥0d (P, Q) \ geq 0d (P, Q) ≥0 для всех точек P, Q P, QP, Q с равенством тогда и только тогда, когда P = QP = QP = Q
   2. d (P, Q) = d (Q, P) d (P, Q) = d (Q, P) d (P, Q) = d (Q, P) для всех точек P, QP, QP, Q
   3. d (P, Q) ≤d (P, R) + d (R, Q) d (P, Q) \ leq d (P, R) + d (R, Q) d (P, Q) ≤d (P, R) + d (R, Q) для всех точек P, Q, RP, Q, RP, Q, R.

   Каково расстояние между точками (0,5) (0,5) (0,5) и (0,13) (0,13) (0,13)?

   ---

   Обратите внимание, что обе эти точки лежат на оси yyy, и поэтому расстояние между точками является абсолютной величиной разности yyy-координат, которая составляет ∣5−13∣ = ∣ − 8∣ = 8.□ \ lvert 5-13 \ rvert = \ lvert -8 \ rvert = 8. \ _ \ Square∣5−13∣ = ∣ − 8∣ = 8. □
   

   Для обобщения вышеуказанной проблемы, если две точки P1 = (x1, y1) P_1 = (x_1, y_1) P1 = (x1, y1) и P2 = (x2, y2) P_2 = (x_2, y_2) P2 = (X2, y2) имеют одинаковую координату xxx, т. е. x1 = x2x_1 = x_2x1 = x2, тогда расстояние между двумя точками равно d (P1, P2) = ∣y1 − y2∣ d (P_1 , P_2) = | y_1-y_2 | d (P1, P2) = ∣y1 −y2 ∣, а отрезок P1P2‾ \ overline {P_1P_2} P1 P2 является вертикальным отрезком.

   Аналогично, если P1P_1P1 и P2P_2P2 имеют одинаковую yyy-координату (y1 = y2y_1 = y_2y1 = y2), то d (P1, P2) = ∣x1 − x2∣d (P_1, P_2) = | x_1- x_2 | d (P1, P2) = ∣x1 −x2 ∣, а отрезок P1P2‾ \ overline {P_1P_2} P1 P2 — горизонтальный отрезок.

   Найдите площадь прямоугольника в плоскости xyxyxy с вершинами

   A = (6, −3), B = (6,7), C = (2,7) и D = (2, −3). A = (6, -3), B = (6, 7), C = (2, 7), \ text {и} D = (2, -3). A = (6, −3), B = (6,7), C = (2,7) и D = (2, −3).

   ---

   Точки AAA и BBB имеют одинаковую xxx-координату, что означает d (A, B) = ∣7 — (- 3) ∣ = 10d (A, B) = \ lvert 7 — (-3) \ rvert = 10d ( A, B) = ∣7 — (- 3) ∣ = 10. Точки BBB и CCC имеют одинаковую yyy-координату, откуда d (B, C) = ∣6−2∣ = 4d (B, C) = \ lvert 6-2 \ rvert = 4d (B, C) = ∣6− 2∣ = 4.Мы проверяем, что точки CCC и DDD имеют одинаковую xxx-координату, а DDD и AAA имеют одинаковую yyy-координату, что означает, что точки действительно являются вершинами прямоугольника.

   Тогда площадь прямоугольника равна [ABCD] = AB⋅BC = 4⋅10 = 40. □ [ABCD] = AB \ cdot BC = 4 \ cdot 10 = 40. \ _ \ square [ABCD] = AB⋅BC = 4⋅10 = 40. □

   Видео-вопрос: Нахождение перпендикулярного расстояния от заданной точки до прямой в двух заданных точках

   Стенограмма видео

   Найдите с точностью до одного десятичного знака расстояние по перпендикуляру от точки отрицательные три, отрицательные четыре, ноль до точки линия на точках один, три, один и четыре, три, два.

   Давайте начнем с того, что напомним, что мы получилась линия, проходящая через точки 𝐴 и 𝐵. Кратчайшее расстояние от третьего точка 𝐶 до линии — это расстояние по перпендикуляру от этой точки. И на самом деле существует ряд способы, которыми мы можем вычислить это расстояние.

   Прежде чем мы это сделаем, давайте определим 𝐴 как точка с координатами один, три, один и 𝐵 как точка с координатами четыре, три, два.𝐶 имеет координаты отрицательные три, отрицательные четыре, ноль. Но мы начнем с поиска уравнение прямой, проходящей через и.

   Мы будем использовать вектор уравнение прямой. Учитывая, что строка содержит точка с вектором положения, а сама линия имеет вектор направления, тогда уравнение прямой равно 𝐚 плюс 𝑡 умножить на.

   В нашем случае мы знаем, что точка на нашей линии имеет координаты один, три, один.Итак, вектор позиции один, три, один. И уравнение нашей прямой равно единице, трем, одному плюс 𝑡 вектора направления. А это вектор 𝐀𝐁.

   Теперь, конечно, чтобы найти вектор направления 𝐀𝐁, мы вычитаем вектор положения 𝐎 из положения вектор. Это 𝐎𝐁 минус 𝐎𝐀, то есть четыре, три, два минус один, три, один. Конечно, мы можем вычесть отдельные компоненты каждого вектора.И мы находим, что вектор 𝐀𝐁 равен три, ноль, один. Теперь у нас есть вектор линии проходящие через точки 𝐀 и. Один, три, один плюс раза три, ноль, один.

   Мы освободили место для следующий шаг. Следующее, что мы собираемся сделать, это найти точку на прямой, где перпендикуляр из 𝐶 пересекает прямую как точка 𝐷. Тогда можно сказать, что позиция вектор — это вектор 𝐎𝐃 — равен один плюс три 𝑡, три плюс ноль 𝑡 и один плюс 𝑡.По сути, мы разбили отдельные компоненты нашей линии в 𝑥-, 𝑦- и 𝑧-координатах. И так это упрощает до одного плюса три 𝑡, три и один плюс 𝑡.

   А это значит, что теперь мы можем найти вектор, который переводит нас из 𝐶 в. В этом разница между вектор 𝐎𝐃 и 𝐎𝐂. Это, конечно, один плюс три 𝑡, три, один плюс минус минус три, минус четыре, ноль. И это упрощается до четырех с плюсом три 𝑡, семь и один плюс 𝑡.

   И вот, на этом этапе у нас есть несколько вариантов. Мы знаем, что векторы, соединяющие 𝐴 к 𝐵 и от 𝐶 к 𝐷 перпендикулярны. Итак, мы могли использовать точечный продукт и говорят, что это означает, что скалярное произведение векторов 𝐀𝐁 и 𝐂𝐃 равно нуль.

   В качестве альтернативы мы могли бы использовать формула расстояния. Мы знаем, что величина 𝐂𝐃 равен квадратному корню из суммы квадратов его отдельных составные части.Итак, это квадратный корень из четырех плюс три 𝑡 в квадрате плюс семь в квадрате плюс один плюс в квадрате.

   Раздаем скобки внутри этого корня. А когда мы упрощаем, мы обнаруживаем, что величина — это квадратный корень из 10𝑡 в квадрате плюс 26𝑡 плюс 66. Теперь, конечно, мы знаем, что расстояние по перпендикуляру от точки до нашей линии — самое короткое из возможных расстояние. Итак, что мы могли сделать на самом деле, так это посмотрите, чтобы минимизировать значение величины 𝐂𝐃.

   Когда мы хотим минимизировать или найдем минимум, продифференцируем по. Конечно, чем меньше число, тем меньше квадратный корень. Так что на самом деле мы только хотим дифференцировать 10𝑡 в квадрате плюс 26𝑡 плюс 66. Мы будем дифференцировать термин по срок. Производная 10𝑡 в квадрате с по отношению к 𝑡 составляет два раза по 10𝑡, что составляет 20𝑡. Производная 26𝑡 равна 26, а производная 66 равна нулю.

   Чтобы найти критическую точку, мы установите его равным нулю и решите относительно. И когда мы это сделаем, вычитая 26 из обе стороны и разделив на 20, мы находим, что negative равно отрицательному 26 больше 20, что равно отрицательный 1. {\ large {\ circ}}}} \)
   — измеряется по часовой стрелке с севера

   Я собрал некоторые из полученных мной вопросов в разделе комментариев ниже.Вы также можете задать эти вопросы, чтобы лучше понять эту тему.

   Чтобы проверить свой ответ, вы можете просмотреть решения, которые я опубликовал в видео на Youtube или в сообщениях Instagram.

   Вы можете подписаться, поставить лайк или подписаться на мой канал на YouTube и аккаунт IG. Я буду продолжать обновлять свой ежедневный пост в IG, желательно.

   Кроме того, ниже вы можете найти некоторые примеры и другие методы! знак равно
   \ (\\ [1pt] \)

   ---

   ВОПРОСЫ ОТ СТУДЕНТОВ:

   \ ({\ small 1.{\ large {\ circ}}} \). Найдите расстояние от его исходного положения.
   
   Ознакомьтесь с моим решением здесь:
   \ (\\ [1pt] \)
   https://youtu.be/I2QdTbg_7-M
   \ (\\ [1pt] \)
   Не забудьте подписаться и подписаться мой канал на YouTube для других видео решений!
   
   \ (\\ [1pt] \)
   \ ({\ small 2. \ enspace} \) Лодка плывет по четырехугольному маршруту ABCD , начиная с A до B в 4 км к востоку. из A , C находится в 3 км к югу от B и D в 4 км S50W от C .{\ large {\ circ}}} \) из города F . Расстояние от F до H составляет 65 км.
   \ (\\ [1pt] \)
   Рассчитайте с точностью до км фактическое расстояние GH .
   \ (\\ [1pt] \)
   Вычислите с точностью до градуса подшипник H от G .
   
   Ознакомьтесь с моим решением здесь:
   \ (\\ [1pt] \)
   https://www.instagram.com/p/CMU0DKEllAC/
   \ (\\ [1pt] \)
   Следите за моим Instagram ежедневно обновления по многим другим решениям и по другим темам!
   
   \ (\\ [1pt] \)
   \ ({\ small 5.{\ large {\ circ}}} \). Вычислить,
   \ (\\ [1pt] \)
   \ ({\ small \ hspace {1.2em} \ left (\ textrm {a} \ right). {\ large {\ circ}}} \) соответственно.{\ large {\ circ}}} \).
   \ (\\ [1pt] \)
   \ ({\ small \ hspace {1.2em} \ left (\ textrm {a} \ right). \ Hspace {0.8em}} \) Как далеко друг от друга находятся два корабля? ?
   \ ({\ small \ hspace {1.2em} \ left (\ textrm {b} \ right). \ Hspace {0.8em}} \) Какой пеленг у B и A ?
   
   Ознакомьтесь с моим решением здесь:
   \ (\\ [1pt] \)
   https://www.instagram.com/p/CMgdBoclhWh/
   \ (\\ [1pt] \)
   Ежедневно подписывайтесь на мой instagram обновления по многим другим решениям и по другим темам!
   

   \ (\\ [1pt] \)

   ---

   ПРИМЕР:

   \ ({\ small 1.{\ large {\ circ}}} \).
   \ ({\ small \ hspace {1.2em} \ left (b \ right). \ Hspace {0.8em}} \) Вычислить
   \ ({\ small \ hspace {2.8em} \ left (i \ right). \ hspace {0.7em}} \) расстояние AB,
   \ ({\ small \ hspace {2.8em} \ left (ii \ right). \ hspace {0.7em}} \) пеленг A из B,
   \ ({\ small \ hspace {2.8em} \ left (iii \ right). \ hspace {0.5em}} \) площадь треугольника ABC,
   \ ({\ small \ hspace {2.8em} \ left (iv \ right). \ Hspace {0.7em}} \) кратчайшее расстояние от B до AC.{\ large {\ circ}}} \), вычислите высоту H над D.
   \ (\ [1pt] \)
   
   
   \ ({\ small \ hspace {1.2em} \ left (a \ right). \ enspace} \) Доказательство. Нарисуйте вертикальную линию под точкой C и назовите точку на вертикальной линии M . Также назовите точку к северу от точки A как Q и точку к северу от точки B как V .
   \ (\\ [1pt] \)
   
   \ (\\ [1pt] \)
   \ (\\ [5pt] \ hspace {1.{\ large {\ circ}}}} \)
   \ (\\ [15pt] \ hspace {3.8em} {\ small \ приблизительно \: 16.67 \ \ mathrm {km}} \)
   \ (\\ [10pt ] {\ small \ hspace {1.2em} \ left (b \ right). \; (ii). \ enspace} \) Пеленг A от B \ ({\ small = \:?} \ )
   \ (\\ [12pt] \ hspace {1. {\ large {\ circ}}} \) на скорости 15 миль в час.{\ large {\ circ}}} \). Рассчитайте расстояние между A и B в 15 00 часов.
   \ (\\ [1pt] \)
   
   \ (\\ [1pt] \)

   \ ({\ small 2. \ Enspace} \) Самолет находится в 120 милях к северу и в 85 милях к востоку от аэропорта. Если пилот хочет лететь прямо в аэропорт, какой пеленг ему следует принимать?

   \ ({\ small 3. \ Enspace} \) Огайо находится в 190 милях к северу от Вирджинии. Стэмфорд находится к востоку от Огайо и в 460 милях от Вирджинии. Какой угол пеленга по направлению от Вирджинии до Стэмфорда? Какой угол пеленга от Стэмфорда до Вирджинии?

   \ ({\ small 4.\ Enspace} \) D находится в 30 км к востоку от A . Корабль плывет от A на определенном пеленге 15 км до B . Затем он плывет к C , что в 40 км от A и к северу от D . Наконец, он плывет прямо на юг к D . AB — биссектриса \ ({\ small \ angle {EAC}} \). Рассчитайте общее расстояние за всю поездку.
   \ (\\ [1pt] \)
   
   \ (\\ [1pt] \)

   \ ({\ small 5. \ enspace} \) Наблюдатель на радиолокационной станции замечает самолет прямо к северу от него и в дальность действия 50 км по горизонтали.{\ large {\ circ}}} \). Рассчитайте скорость самолета в км / ч.

   \ ({\ small 6. \ Enspace} \) N к северу от S . NS — касательная к окружности, радиус 1 км, в точке T . Мужчина проходит 2 км по кругу от T до P . Какое расстояние и азимут P от T ?
   \ (\\ [1pt] \)
   
   \ (\\ [1pt] \)

   \ ({\ small 7. \ enspace} \) На схеме: A , B , C и D — четыре точки на горизонтальном поле.{\ large {\ circ}}} \), BD \ (= \) 150 м и CD \ (= \) 110 м.
   \ ({\ small \ hspace {1.2em} \ left (a \ right). \ Hspace {0.8em}} \) Найдите значение \ ({\ small \ angle {ADB}} \).

   No related posts.