3,6 М;(АТ + соох-ис) (2.27)
где ¥0 — скорость поезда перед торможением, км/ч; — время подготовки тормозов к действию, с;
К — границы выбранного диапазона скоростей (для ручного расчета диапазон не более 10 км/ч), км/ч;
шох — основное удельное сопротивление движению поезда на холостом ходу локомотива, Н/кН.
Условно считается, что в период времени г„ тормоза в поезде не работают, а по его истечении мгновенно увеличивают тормозное нажатие до максимального. При этом /„ рассчитывается так, чтобы длина тормозного пути в реальном случае и при указанном допущении была одинакова. Если предположить, что работа сил трения соответствует
Рис 2.10. К расчету времени одготовки тормозов к действию
площади под диаграммами наполнения тормозных цилиндров, то выбрав среднюю из них для поезда и заменив на скачкообразную с равенством площадей 51=52 можно найти время *п, как показано на рис. 2.10.
Из рисунка видно, что при удлинении поезда гп увеличивается, а при росте темпов наполнения тормозных цилиндров, например, заменяя пневматические тормоза на электропневматические, гп уменьшается где£> и С- коэффициенты, зависящие от длины поезда и быстродействия тормозной системы [3].
Из выражения (2.27) следует, что для расчета 5П использована формула, предполагающая равномерное движение, которое возможно лишь при равенстве шох=|-/с|. Поэтому учет изменения скорости поезда от уклона на этом отрезке пути сделан за счет корректировки ?п.
Расчет действительного тормозного пути выполняется по частям в каждом диапазоне скоростей от ¥0 до нуля с их последующим суммированием. При этом значения удельных сил в знаменателе вычисляются всякий раз для средней в диапазоне скорости и считаются в нем условно неизменными в соответствии с выражениями
где сох, оо0″, ш„х — основное удельное сопротивление движению локомотива, состава и поезда, Н/кН; а, В, 7 — коэффициенты [3];
ыо8″, шы», («)от» — основное удельное сопротивление движению восьми,четырехосных и других вагонов, Н/кН;
<2%, £>4, — вес восьми-, четырехосных и других групп вагонов в поезде, кН,
/, г,р — коэффициенты [3].
Получив для каждого интервала скоростей отрезки действительных тормозных путей Д5Д, сложив их поочередно от минимальной до максимальной скорости и добавив к результату длину подготовительного пути, получают полное значение тормозного пути.
Таблица 2.2. Результаты расчета длины тормозного пути поезда по интервалам скорости
V, км/ч | Фкр | ьТ1 Н/кН | С | 5„. м | км/ч | Фкр | К Н/кН | Н/кН | 0>х, Н/кН | «ох. Н/кН | -к, Н/кН | м | 1м, м | м |
80 | 0,097 | 32.9 | 15,8 | 352 | 1153 | |||||||||
75 | 0,100 | 33.6 | 5,12 | 1,64 | 1,69 | 28,2 | 221 | 801 | ||||||
70 | 0,120 | 34,6 | 15,6 | 304 | 884 | |||||||||
65 | 0. | 35,6 | 4,6 | 1,48 | 1,54 | 30,1 | 180 | 580 | ||||||
60 | 0,108 | 36,6 | 15,4 | 257 | 657 | |||||||||
55 | 0,112 | 38,0 | 4,1 | 1,35 | 32,2 | 142 | 400 | |||||||
10 | 0,198 | 67,1 | 13,9 | 39 | 6 | |||||||||
5 | 0,227 | 74,6 | 2,5 | 0,96 | 1,01 | 68,5 | 6 | 6 | ||||||
0 |
В связи с заменой реальной диаграммы наполнения тормозных цилиндров на скачкообразную указанный метод дает удовлетворительную точность расчетов при скоростях до 40 км/ч и на спусках до 20 %о. Если остановка поезда происходит до наполнения тормозных цилиндров, то указанная замена диаграмм их наполнения приводит к ошибочному увеличению тормозного пути.
Если остановка поезда происходит до наполнения тормозных цилиндров, то указанная замена диаграмм их наполнения приводит к ошибочному увеличению тормозного пути.
Более точным и универсальным способом расчета длины тормозного пути является метод интегрирования уравнения движения поезда по интервалам времени. В нем изменение скорости ДКв заданном интервале Л1 определяется по выражению
Зная предыдущую расчетному шагу скорость движения У„, и получив среднюю, находят приращение длины тормозного пути Д5, в интервале А1
Расчет шох для средней скорости ведут по выражениям (2.30)-(2.33), как показано выше, а Ь, по формуле (2.29), в которой изменение расчетного тормозного коэффициента во времени для различных видов подвижного состава и способов торможения приведено в таблицах [3].
Полученные таким образом отрезки Д5Т последовательно суммируют для определения полного тормозного пути. Результаты расчетов целесообразно заносить в таблицу, аналогичную таблице 2.3 сданными для пассажирского поезда [3].
Таблица 2.3. Результаты расчета длины тормозного пути поезда по интервалам времени
Дг, с | »Р | Фкр | К Н/кН | Н/кН | ‘с-Н/кН | С. Н/кН | АУ, км/ч | У, км/ч | км/ч | Д5Т, м | «г, м |
0-3 | 0 | 0,09 | 0 | 4,5 | •5 | 0,5 | +0,05 | 100,0′, | 100 | 83 | |
3-6 | 0,21 | 0.09 | 19 | 4,5 | -5 | 18,5 | -1.85 | 98,2 | 99 | 32 | 165 |
6-9 | 0,36 | 0,092 | 33,2 | 4,3 | -5 | 32,5 | 3,3 | 94. | 96 | 80 | 245 |
42-45 | 0,60 | 0,160 | 96 | 1.6 | ■5 | 92,6 | -9,3 | 15,1 | 20 | 17 | 833 |
45-49 | 0,60 | 0,20 | 120 | 1,3 | -5 | 116,3 | -15,1 | 0 | 10 | 11 | 844 |
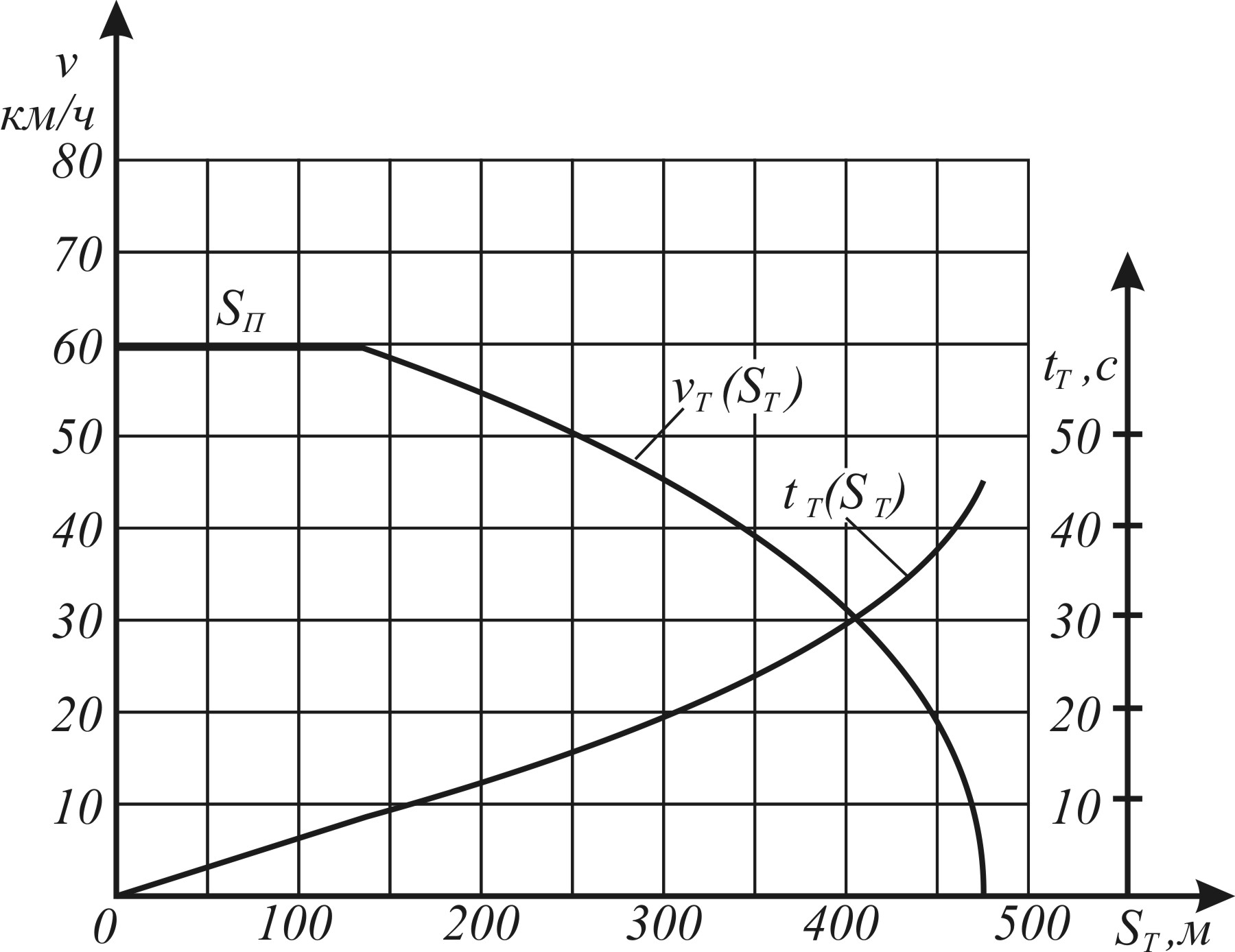
Рис 2.11 Номограмма тормозного пути грузового поезда при композиционных колодках на спуске 10 %о
Известны еще три отечественных метода расчета тормозного пути: аналитический метод расчета интегрированием уравнения движения поезда при установившемся торможении, графический метод и метод расчета по номограммам.
По третьему методу номограммы предварительно рассчитываются на ЭВМ. Полученные таким образом номограммы позволяют графически решать ряд следующих тормозных задач в соответствии с рис. 2.11:
— определение длины тормозного пути по известным значениям тормозного расчетного коэффициента и скорости движения;
— определение необходимого тормозного расчетного коэффициента по заданным длине тормозного пути и скорости движения;
— определение допустимой скорости движения по установленным длине тормозного пути и тормозному расчетному коэффициенту.
В связи с большим количеством отличий в условиях торможения, таких, например, как категория поезда, типы используемых тормозных колодок, вид применяемых тормозов, величина уклона и т.д., полный набор номограмм для всех случаев подготовить проблематично. Это ограничивает возможности их применения.
Это ограничивает возможности их применения.
Доступность и высокий уровень развития вычислительной техники в настоящее время позволяют по разработанным программам
расчета тормозного пути — численным интегрированием по интервалам времени легко решить любую тормозную задачу. Ранее этот метод применялся как контрольный и наиболее универсальный для проверки точности расчета другими методами.
⇐Предыдущая Оглавление Следующая⇒
4.2 Расчет тормозного пути поезда при экстренном торможении
При расчетах тормозной путь поезда принимаемравным сумме подготовительного и действительного путей торможения, м, по формуле 4.7:
Sт=Sп+Sд (4.7)
Подготовительный тормозной путьSп, м, определяем по формуле 4.8:
Sп=0,278Vmaxtп, (4. 8)
8)
где Vmax– скорость поезда в начале торможения (максимальная), км/ч;
tп– время подготовки тормозов к действию, с.
Vmax=70 км/ч.
При расчетах tп для грузового поезда до 300 осей принимаем формулу 4.9:
, (4.9)
где iс– приведенный уклон,0/00;
bm– удельная тормозная сила поезда при максимальной скорости, кгс/тс.
iс=80/00
Для уклона в выражении 4.9 берётся знак «+».
При экстренном торможении в формулу 4.9 подставляем bm=48,78 кгс/тс:
с
При служебном торможении в формулу 4.9 подставляем 0,8bm=39,024 кгс/тс:
с
Подставляем полученные значения в
формулу 4. 8. Для экстренного торможения:
8. Для экстренного торможения:
Sп=0,278×70×12,15=236,44 м
Для служебного торможения:
Sп=0,278×70×13,756=247,142 м
Суммарный действительный тормозной путь (определяем по интервалам в 10 км/ч, таблица 4.1), м, определяем по формуле 4.10:
(4.10)
Рассчитаем действительный тормозной путь для первого интервала (0–10) км/ч при экстренном торможении:
м
Аналогично рассчитывается действительный тормозной путь при экстренном и при служебном торможениях для всех остальных интервалов.
Суммарный действительный тормозной путь при экстренном торможении рассчитывается как сумма полученных результатов по формуле 4.10:
м
Суммарный действительный тормозной путь при служебном торможении рассчитывается как сумма полученных результатов по формуле 4.10:
м
Полученные значения подставляем в
формулу 4. 7. Для экстренного торможения:
7. Для экстренного торможения:
Sт=236,44+415,62=652,06 м
Для служебного торможения:
Sт=247,142+534,383=781,525 м
4.3 Расчет тормозного пути поезда при полном служебном торможении
Полученные в подпункте 4.2 значения полного тормозного пути при экстренном и полном служебном торможении сравниваем с нормируемыми (допустимыми) значениями по таблице 4.2.
Таблица 4.2. – Нормируемый тормозной путь для поезда
Вид поезда | Скорость поезда V, км/ч | Нормируемый тормозной путь, м | |
ic≤60/00 | 60/00≤ic≤100/00 | ||
Грузовой | Менее 80 | 1000 | 1200 |
80-90 | 1300 | 1500 | |
90-100 | 1600 | 2000 | |
Пассажирский | Менее 100 | 1000 | 1200 |
100-140 | 1200 | 1300 | |
140-160 | 1600 | 1700 | |
Для заданных значений (Vmax=70
км/ч,ic=8‰)
нормируемый тормозной путь составляет
1000м, т. о. расчетные значения тормозного
пути при экстренном и полном служебном
торможении соответствуют допустимым.
о. расчетные значения тормозного
пути при экстренном и полном служебном
торможении соответствуют допустимым.
График зависимости пути при экстренном и полном служебном торможении от скорости движения поезда приведен в приложении Б.
5 Результаты расчетов на пэвм
Таблица 5.1- Формирование поезда
Определение веса состава | |
Весовая доля в составе вагонов по типу подшипникового узла: | |
подшипники скольжения, β1 | |
подшипникикачения, β2 | 1,000 |
Основное удельное сопротивление движению локомотива , кгс | 2,928 |
Основное сопротивление движению состава, кгс/тс | 1,112 |
Расчетный вес состава,тс | 5241,009 |
Удельное сопротивление троганию состава с места , кгс/тс; | 1,000 |
Вес состава по условию трогания с места ,тс | 8757,333 |
Определение числа вагонов в составе | |
Количество вагонов: | |
грузового поезда, 4-осные | 31,196 |
грузового поезда, 4-осные | 14,558 |
грузового поезда, 8-осные | 4,679 |
Таблица 5. 2 – Назначение типов вагонов
2 – Назначение типов вагонов
Вес полученного состава,тс | 5282 |
Разница между весом полученного состава и расчетным весом , тс | 40,991 |
Длина поезда , м | 841,2 |
, м | 358,8 |
«Условие по длине выполнено. Во всех дальнейших расчетах принимается вес состава , полученный в этом столбце»
Таблица 5.3 – Обеспечение поезда тормозами
Расчет рычажной тормозной передачи вагона | |
Площадь поршня тормозного цилиндра ,см2 | 995,382 |
Продолжение
таблицы 5. | |
Усилие отпускной пружины , кгс | 224,4 |
Реактивное усилие возвратной пружины авторегулятора , кгс | 231,923 |
Общее передаточное число рычажной передачи | 8,961 |
Действительная суммарная сила нажатия на все тормозные колодки вагона , кгс | 30148,351 |
Коэффициент силы нажатия на тормозные колодки вагона | 0,355 |
Усилие по штоку поршня тормозного цилиндра , кгс | 3738,218 |
Оценка обеспеченности поезда тормозами | |
Число вагонов той же осности, что и рассчитываемый вагон, n | 32 |
Осность рассчитываемого вагона | 4 |
Расчетная сила нажатия на ось локомотива , тс | 5 |
Потребный тормозной коэффициент грузового поезда | 0,3 |
Суммарное число осей вагонов, рассчет которых не производился, n0 | 122 |
Фактический тормозной коэфициент для грузового поезда | 0,31 |
«Поезд тормозами обеспечен»
Таблица 5. 4 – Проверка поезда на возможность
разрыва при экстренном торможении
4 – Проверка поезда на возможность
разрыва при экстренном торможении
Суммарная действительная сила нажатия на все тормозные колодки состава , кгс | 610000,000 |
Суммарная действительная сила нажатия на тормозные колодки локомотива, кгс | 1024747,328 |
Коэффициент трения тормозных колодок вагонов при Vmax | 0,273 |
Коэффициент трения тормозных колодок вагонов при Vmin | 0,315 |
Коэффициент трения тормозных колодок локомотива при Vmax | 0,102 |
Коэффициент трения тормозных колодок локомотива при Vmin | 0,15 |
Максимальные продольно-динамические усилия для сжатого поезда R1при Vmax | 9433 |
Максимальные продольно-динамические усилия для сжатого поезда R2при Vmin | 12036 |
Максимальные продольно-динамические усилия для растянутого поезда R3при Vmax | 15328 |
Максимальные продольно-динамические усилия для растянутого поезда R4при Vmin | 19558 |
Таблица 5. 5- Результаты расчёта замедляющих
усилий (расчёт на ПЭВМ)
5- Результаты расчёта замедляющих
усилий (расчёт на ПЭВМ)
| Интервал скорости Vн –Vк | Vmax | |||||||
0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70 | ||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
Vср,км/ч | 5 | 15 | 25 | 35 | 45 | 55 | 65 | 70 | |
х,, кгс/тс | 2,464 | 2,644 | 2,894 | 3,214 | 3,604 | 4,064 | 4,594 | 4,885 | |
Рх, кгс | 679,995 | 729,675 | 798,675 | 886,995 | 994,635 | 1121,6 | 1267,88 | 1348,26 | |
, кгс/тс | 0,972 | 1,039 | 1,13 | 1,244 | 1,382 | 1,543 | 1,728 | 1,819 | |
, кгс | 5135,02 | 5488,16 | 5966,3 | 6569,46 | 7297,62 | 8150,79 | 9128,96 | 9609,467 | |
, кгс | 5815,01 | 6217,83 | 6764,98 | 7456,45 | 8292,25 | 9272,38 | 10396,8 | 10957,727 | |
, кгс/тс | 1,046 | 1,119 | 1,217 | 1,342 | 1,492 | 1,668 | 1,871 | 1,972 | |
0,349 | 0,33 | 0,315 | 0,303 | 0,293 | 0,284 | 0,276 | 0,273 | ||
0,227 | 0,177 | 0,15 | 0,133 | 0,12 | 0,112 | 0,105 | 0,102 | ||
,тс | 212,738 | 201,3 | 192,15 | 184,664 | 178,425 | 173,146 | 168,621 | 166,593 | |
,тс | 232,413 | 181,819 | 153,712 | 135,826 | 123,443 | 114,362 | 107,418 | 104,524 | |
, тс | 445,15 | 383,119 | 345,862 | 320,489 | 301,868 | 287,508 | 276,039 | 271,117 | |
bm, кгс/тс | 80,092 | 68,931 | 62,228 | 57,663 | 54,312 | 51,729 | 49,665 | 48,78 | |
0,8bm, кгс/тс | 64,073 | 55,145 | 49,782 | 46,13 | 43,45 | 41,383 | 39,732 | 39,024 | |
bm + ох—ic, кгс/тс | 74,138 | 63,05 | 56,445 | 52,004 | 48,804 | 46,397 | 44,536 | 43,751 | |
0. | 58,12 | 49,264 | 43,999 | 40,472 | 37,942 | 36,051 | 34,603 | 33,995 | |
Δ, м | 5,619 | 19,822 | 36,903 | 56,076 | 76,825 | 98,769 | 121,606 |
| |
Δ, м | 7,168 | 25,37 | 47,342 | 72,055 | 98,82 | 127,114 | 156,514 |
| |
Таблица 5. 6 –Расчет тормозного пути при
экстренном торможении
6 –Расчет тормозного пути при
экстренном торможении
Время подготовки тормозов к действию при экстренном торможении, с | 12,153 |
Подготовительный тормозной путь при экстренном торможении , м | 236,488 |
Действительный тормозной путь при экстренном торможении , м | 415,621 |
Тормозной путь при экстренном торможении , м | 652,110 |
Таблица 5.7– Расчет тормозного пути при полном служебном торможении
Время подготовки тормозов к действию при экстренном торможении, с | 12,691 |
Подготовительный тормозной путь при экстренном торможении, м | 246,96 |
Действительный тормозной путь при экстренном торможении , м | 534,381 |
Тормозной путь при экстренном торможении , м | 781,342 |
«Тормозной
путь в норме. Расчет закончен»
Расчет закончен»
Расчет тормозного пути по интервалам скорости
Наиболее распространенным при практическом использовании является аналитический метод расчета длины тормозного пути, опирающийся на численное интегрирование уравнения движения поезда (2.4) по интервалам скорости. При этом тормозной путь 5Т для упрощения расчетов разбивается на два участка: подготовительный 5П и действительный 5Д.
Условно считается, что при прохождении поездом участка 5П тормоза не работают, а на участке 5Д они действуют с максимальным и неизменным давлением в ТЦ, которое возникает скачкообразно. Участок 5П и время 1п, за которое его проходит поезд, рассчитываются таким образом, чтобы путь 5Т, полученный указанным способом, соответствовал вычисляемому с учетом реального нарастания давления в ТЦ.
Расчет длины тормозного пути выполняется по следующей формуле где — скорость поезда перед торможением, км/ч;
Ун, Ук — начальная и конечная скорости поезда в выбранном интервале скоростей, км/ч;
£ — замедление поезда под действием единичной удельной силы, кмкН/(ч2Н) (для вагонов составляет 120, тепловозов — 114, электровозов — 107, электропоездов — 119), а при расчетах для грузовых и пассажирских поездов принимается £ = 120; Ьт — удельная тормозная сила, Н/кН;
<о0х — основное удельное сопротивление движению поезда, Н/кН; 1с — удельное сопротивление от спрямленного уклона с учетом сопротивления в кривой, %о.
Так как в (9.9) входят сложные нелинейные функции, характеризующие процесс торможения и одновременно зависящие от него, то расчет второго слагаемого ведется пошагово методом численного интегрирования. При этом в выбранном интервале скоростей (для счета вручную обычно Д V = 10 км/ч, на ПЭВМ Д V = 5 км/ч) удельные силы Ьт, (о$х, 1с условно принимаются неизменными и равными для средней скорости в данном интервале. После чего рассчитывается часть длины действительного тормозного пути 5Д. Последовательно суммируя эти части от минимальной скорости до выбранной и прибавляя к ним соответствующие значения 5П можно получить зависимость длины тормозного пути данного поезда от скорости его торможения 5Т =ЛУ). Результаты расчетов удобно записывать в форме таблицы, аналогичной табл. 9.2 (для ориентировки в ней приведены данные, соответствующие характеристикам груженого грузового поезда).
Как видно из (9.9), для расчета 5П использована формула, предполагающая равномерное движение поезда, которое возможно лишь при условии со0д. = [-у. Поэтому учет изменения скорости поезда в зависимости от уклона на этом отрезке пути сделан за счет корректировки *п. Кроме того, на это время влияют длина поезда, время наполнения ТЦ и значение Ьт Таблица 9.2
= [-у. Поэтому учет изменения скорости поезда в зависимости от уклона на этом отрезке пути сделан за счет корректировки *п. Кроме того, на это время влияют длина поезда, время наполнения ТЦ и значение Ьт Таблица 9.2
Результаты расчетов длины тормозного пути поезда весом А», кН, на спуске У, %с
V, км ч | Н кН | с | 5П, м | Уф, км ч | Н кН | Н кН | Н кН | Шип Н кН | Н кН | Д5Д, м | 2>я-/.и м | 5„ м | ||
80 | 0,097 | 32,9 | 15,8 | 352 | 75 | 0,100 | 33,6 | 1,64 | 52 | 1,69 | 282 | 221 | 801 | 1153 |
70 | 0,102 | 34,6 | 15,6 | 304 | 65 | 0,105 | 35,6 | 1,48 | 4,6 | 1,54 | 30,1 | 180 | 580 | 884 |
60 | 0,108 | 36,6 | 15,4 | 257 | 55 | 0,112 | 38,0 | 135 | 4,1 | 1,40 | 32Д | 142 | 400 | 657 |
,ю | 0,198 | 67,1 | 13,9 | 39 | 5 | 0227 | 74,6 | 0,% | 2^ | 1,01 | 68,5 | 6 | 6 | 45 |
Обобщенная формула для расчета времени подготовки тормозов к действию имеет вид
(9. Ю)
Ю)
Коэффициенты А и Р для грузовых поездов с количеством осей 200 соответственно равны 7 и 10; от 200 до 300 — 10 и 15; более 300 осей — 12 и 18; для пассажирских поездов и одиночно следующих локомотивов с пневматическими тормозами — 4 и 5; для пассажирских поездов с ЭПТ — 2 и 3. При автостопном торможении рассчитанное время 1п увеличивается на 14 с. В формулах (9.5), (9.6) значение 1с принимается для спусков со знаком минус, для подъемов со знаком плюс.
Таким образом, последовательно применяя формулы (3.12), (3.11), (3.10), (3.13) и (9.10), определяют *п. Из (9.9) находят 5П, занося в табл. 9.2 соответствующие значения рассчитанных параметров. Для расчета действительного тормозного пути в выбранном интервале скоростей определяют среднюю и для нее рассчитывают Ьт (как показано выше по формуле (3.13) и основное удельное сопротивление движению щх.
Основным сопротивление движению называют потому, что оно присутствует на подвижном составе всегда и проявляется в виде сил трения между колесами и рельсами, в буксовых узлах и набегающей воздушной среде. К дополнительному сопротивлению относятся, например, сопротивление, возникающее при подъеме, в кривом участке пути, при ветре и низкой температуре, при работе подвагонного генератора, при трогании с места и ряд других, которые могут возникать на подвижном составе в процессе его эксплуатации.
Поскольку сопротивление движению в соответствии с молеку-лярно-механической природой сил трения существенно зависит от приложенной нагрузки, то для расчетов используют его удельное значение, приходящееся на единицу веса транспортного средства. Таким образом, несмотря на то что удельное сопротивление движению, например, порожнего вагона больше, чем груженого, полное сопротивление последнего будет, конечно, выше. Это объясняется тем, что темп падения удельного сопротивления с ростом нагрузки оказывается меньше, чем скорость ее увеличения,
Сопротивление перевозке единицы груза в груженом вагоне меньше, чем сопротивление в порожнем. Значит, энергозатраты на проведение по участку загруженного и порожнего поездов одинакового веса при прочих равных условиях для последнего оказываются больше.4»й)о„ — основное удельное сопротивление движению восьми,
четырехосных и других типов вагонов, Н/кН; б8, б4, би — вес соответствующей группы вагонов, кН.
Формулы для расчета со* вагонов различных категорий на звеньевом пути приведены ниже:
— грузовые четырехосные на подшипниках скольжения и шести-осные на роликовых подшипниках в груженом состоянии
— грузовые четырехосные с роликовыми подшипниками в груженом состоянии и вагоны рефрижераторных поездов
— грузовые груженые восьмиосные на роликовых подшипниках
— пассажирские цельнометаллические на роликовых подшипниках Получив для каждого интервала скоростей величины действительных тормозных путей Д5Д и сложив их последовательно от соответствующего минимальной (остановочной) до максимальной (или требуемой для построения графика), заносят в соответствующую графу 5Д табл. 9.2. Наконец, складывая эти значения с ранее рассчитанным для данной скорости движения 5П, получают величину 5Т.
⇐ | Расчет длины тормозного пути | | Автоматические тормоза подвижного состава | | Расчет тормозного пути по интервалам времени | ⇒
Определение длины тормозного пути — Страница 2
Страница 2 из 2
Тормозной путь определяют исходя из скорости движения, расчетного тормозного нажатия н профиля пути С помощью расчетных номограмм тормозного пч’ти при экстренном торможении определяют одно из четырех условий процесса торможения при заданных трех основных (тормозной путь, максимальная начальная скорость торможения, коэффициент расчетного тормозного нажатия, уклон). При расчете тормозного пути полного служебного торможения удельную тормозную силу уменьшают на 20%.
Таблица 247 Формулы для расчета длины тормозных путей и величины замедления поезда
Примечания I Номограммы величины тормозного пути в зависимости от расчетного тормозного коэффициента и скорости в начале торможения приведены для грузовых поездов на рис 315 и 316 и для пассажирских — на рис. 317 и 318.
- Номограмма величины тормозного пути в зависимости от скорости движения и среднее замедления поезда приведена на рис. 319.
- Величина среднего замедления представляет собой удельную кинетическую энергию, приходящуюся на единицу массы, которая гасится тормозной системой на единице длины тормозною пути:
для пассажирских и моторвагонных поездов на площадке для грузовых и пассажирских поездов
где ?τ — время от начала торможения до полной остановки поезда
- Расчетный коэффициент сцепления колес с рельсами определяют по формуле
где о — средняя нагрузка от колесной пары на рельсы Значение функции скорости см на рис 320
Таблица 248. Величина замедления ς, км/ч2 под действием удельной замедляющей силы 1 кгс/т
Подвижной состав |
Замедление |
Грузовые и пассажирские поезда Одиночно следующие локомотивы: |
120 |
паровозы |
121 |
тепловозы |
114 |
электровозы |
107 |
Электропоезда |
119 |
Дизель-поезда |
116 |
Рис. 315. Номограмма величины тормозного пути грузового поезда при чугунных колодках:
а — на площадке, б -на спуске 0,006, в — на спуске 0,010
Рис. 316. Номограмма величины тормозного пути грузового поезда при композиционных тормозных колодках: а — на площадке; б — на спуске 0,006; в — на спуске 0,010
Рис. 317. Номограмма величины тормозного пути пассажирского поезда при чугунных тормозных колодках (сплошные линии — электропневматическое торможение, штриховые — пневматическое):
а — на площадке, б — на спуске 0,006, в — на спуске 0,010
Рис. 318. Номограмма величины тормозного пути пассажирского поезда при композиционных тормозных колодках (сплошные линии — электропневматическое торможение, штриховые — пневматическое): а — на площадке; б — на спуске 0,006, в — на спуске 0,010
Рис. 319. Номограмма величины тормозного пути в зависимости от скорости и замедления поезда на площадке
Таблица 249. Формулы для определения времени подготовки тормозов к действию
Тип поезда |
Время подготовки tп, с |
Грузовой состав длиной до 200 осей при пневматических тормозах |
1 При срабатывании автостопа время подготовки тормозов к действию увеличивается на 12 с
Таблица 250. Формулы для определения коэффициентов трения тормозных колодок о колесо
Таблица 251. Расчетный коэффициент трения тормозной колодки о колесо
Примечание Действительный коэффициент трения тормозной колодки о колесо определяется по формулам: где К — действительная сила нажатия тормозной колодки на колесо, тс.
Таблица 252. Расчетная сила нажатия тормозной колодки на колесо Кр в зависимости от действительной силы нажатия К
Примечание. Действительная сила нажатия тормозной колодки на колесо определяется по формуле K = Fpm\u, кгс, где h -площадь поршня тормозного цилиндра, см2, р — давление сжатого воздуха в тормозном цилиндре, кгс/см2; п — передаточное число рычажной передачи до колодки; нп — коэффициент полезного действия рычажной передачи (с учетом влияния усилия отпускной пружины).
Т а блица 253. Расчетный коэффициент сцепления, принимаемый для проверки отсутствия заклинивания колесных пар и рекомендуемый при проектировании тормозного оборудования
Расчетная скорость, км/ч |
Расчетный коэффициент сцепления при нагрузке от колесной пары на рельсы, тс |
||||
6 |
10 |
15 |
20 |
25 |
|
Пассажирские, изотермические вагоны, вагоны электро- и дизель-поездов |
|
|
|
|
|
40 |
0,140 |
0,135 |
0,130 |
0,124 |
__ |
120 |
0,110 |
0,107 |
0,102 |
0,097 |
— |
140 |
0,106 |
0,102 |
0,098 |
0,094 |
__ |
160 |
0,101 |
0,097 |
0,094 |
0,090 |
__ |
Грузовые вагоны |
|
|
|
|
|
20 |
0,31 |
0,125 |
0,121 |
0,116 |
0,110 |
100 |
0,097 |
0,094 |
0,090 |
0,086 |
0,081 |
120 |
0,092 |
0,090 |
0,085 |
0,081 |
0,070 |
Локомотивы |
|||||
20 |
— |
__ |
0,132 |
0,126 |
0,119 |
100 |
— |
_ |
0,097 |
0,093 |
0,088 |
160 |
— |
— |
0,087 |
0,083 |
0,078 |
Таблица 254. Тормозной путь, м, проходимый поездом при проверке действия тормозов с начальной скорости
Крутизна спуска |
Скорость, км/ч |
||||
40 |
60 |
80 |
100 |
120 |
|
0 |
125/250* |
220/450 |
330/650 |
400/ — |
555/ — |
0,002 |
140/300 |
245/500 |
260/750 |
490/ — |
620/ — |
0,004 |
150/350 |
270/600 |
400/900 |
545/ — |
695/ — |
* Здесь и далее перед чертой — для пассажирских поездов, за чертой — для грузовых.
Таблица 255. Процент расчетного тормозного нажатия от максимального при ступенях торможения и чугунных тормозных колодках в грузовом поезде
Режим включения воздухораспределителя |
Величина снижения давления в тормозной магистрали, кгс/см2 |
||
0,65 |
0,75 |
0,95 |
|
Порожний |
65 |
75 |
90 |
Средний |
45 |
57 |
75 |
Груженый |
30 |
50 |
70 |
Рис. 320. Функция скорости для определения расчетного коэффициента сцепления колес с рельсами:
1 — пассажирский подвижной состав и вагоны на тележках пассажирского типа; 2 — локомотивы; 3 — грузовые вагоны
Рис. 321. Перепад давления Δρ в тормозной магистрали в зависимости от ее длины (м), утечки (л/мин), приходящейся на I м длины магистрали, и зарядного давления:
1 — 6,2 кгс/см2; 2 — 5,5 кгс/см2, 3 — 4,8 кгс/см2
Рис. 322. Зависимость величины зарядного давления в тормозной магистрали грузового поезда при установленном минимальном давлении в его хвостовой части от длины магистрали и равномерно распределенных утечек величиной:
1 — 2 л/мин · м; 2 — 1,4 л/мин · м; 3 — 1 л/мин м
- Графический способ определения диаметра калиброванного отверстия в зависимости От объема резервуара и времени истечения из него воздуха в атмосферу через калиброванное отверстие
Таблица 256. Определение времени истечения воздуха из резервуара в атмосферу (рис. 323, 324)
Рис. 323. Номограмма № 1 для определения отношения Vff в зависимости от объема Резервуара и диаметра отверстия
Рис. 324. Номограмма № 2 для определения времени истечения воздуха из резервуара в атмосферу через круглое отверстие в зависимости от отношения Vff (см. рис. 323)
Расчет тормозного пути Методом ПТР.
Расчет тормозного пути Методом ПТР.Полный тормозной путь Sт, проходимый поездом от начала торможения до остановки, принимается равным сумме пути подготовки тормозов к действию Sп и действительного пути торможения Sд.
|
Sт |
= |
Sп |
+ |
ΣSд |
|
|
( 1.11 ) |
Величина пути подготовки тормозов к действию определяется по формуле
|
Sп |
= |
Vнт * tп |
, |
|
|
|
( 1.12 ) |
|
3.6 |
|
|
|
где:
Vнт — скорость поезда в момент начала торможения, км/ч;
tп — время подготовки тормозов поезда к действию, с;
3.6 – переводной коэффициент.
Время подготовки тормозов к действию определяется из условия замены медленного, реального процесса наполнения тормозного цилиндра среднего вагона, мгновенным наполнением до полной величины, при условии равенства тормозных путей, проходимых поездом при реальном и условном наполнении тормозных цилиндров (рис. 1.6).
В зависимости от рода подвижного состава и его длины время подготовки тормозов к действию определяется по формуле
|
tп |
= а — б |
iс |
|
|
|
|
( 1.13 ) |
|
bп |
|
|
|
где:
iс — спрямленный уклон;
bп — удельная тормозная сила.
Величины коэффициентов а и б зависят от рода движения, вида управления тормозами в пассажирском поезде, от длины поезда в осях и принимаются по таблице (1.2).
Величина действительного пути торможения определяется суммированием величин пути торможения в выбираемых интервалах скорости при условии постоянства величин удельных сил, действующих на поезд в этом интервале, по формуле 1.14
|
Sд |
= |
4.17[(Vн)2 – (Vк)2] |
, |
|
|
|
( 1.14 ) |
|
bт + wox + iс |
|
|
|
где:
Vн, Vк - начальная и конечная скорости поезда в принятом интервале скоростей, км/ч;
bт — удельная тормозная сила, кг/т;
wox — удельное основное сопротивление движению поезда, кг/т;
iс - спрямленный уклон, ‰.
Таблица 1.2.
Зависимость коэффициентов а и б от типа поезда
|
Условия выбора величины коэффициента |
а |
б |
|
Пассажирский поезд : |
|
|
С пневматическими тормозами |
4 |
5 |
|
С электропневматическими тормозами |
2 |
3 |
|
Грузовой поезд длиной : |
|
|
|
до 200 осей |
7 |
10 |
|
до 300 осей |
10 |
15 |
|
до 400 осей |
12 |
18 |
|
до 400 осей, если все ВР усл. № 483 |
6 |
8 |
Удельная тормозная сила определяется по формуле
|
bт |
= 1000 * |
φкр * |
υр |
|
, |
|
( 1.15 ) |
где:
υр — расчетный тормозной коэффициент поезда. Он показывает сколько тонн нажатия тормозных колодок приходится на одну тонну веса поезда;
φкр — расчетный коэффициент трения тормозных колодок.
Расчетный тормозной коэффициент поезда с учетом веса и нажатия локомотива вычисляется по формуле
|
υр |
= |
Крл + Крв |
, |
|
|
|
( 1.16 ) |
|
P + Q |
|
|
|
где:
Крл, Крв — сумма расчетных сил нажатия тормозных колодок локомотива и вагонов, т;
Р — вес локомотива;
Q — вес состава.
Сумма расчетных сил нажатия тормозных колодок поезда подсчитывается по формуле или берется из справки формы БУ-45
|
Кр |
= |
n1*Кр1*m1 |
+ |
n2*Кр2*m2 |
+ |
n3*Кр3*m3 + ……. |
( 1.17 ) |
где:
ni – количество однотипных вагонов, оборудованных однотипными колодками;
К – расчетное тормозное нажатие на колодку;
mi – количество колодок на единице подвижного состава.
При определении тормозного коэффициента грузового груженого поезда на спусках до 20 ‰ вес локомотива и нажатие его колодок не учитываются.
Расчетное значение коэффициента трения чугунных колодок определяем по формуле
|
φкр |
= 0.27 |
V + 100 |
|
|
|
|
( 1.18 ) |
|
5V + 100 |
|
|
|
|
Основное удельное сопротивление движению поезда при холостом ходе локомотива может быть подсчитано по формуле
|
Wox |
= |
Wo*Q + Wx*P |
, |
|
|
|
( 1.19 ) |
|
P + Q |
|
|
|
где:
Wo – основное удельное сопротивление движению вагонов;
Wx – основное удельное сопротивление движению локомотива на холостом ходу.
|
Wx |
= |
2.4 |
+ |
0.11*V |
+ |
0.00035*V2 |
( 1.20 ) |
Основное удельное сопротивление движению, например, грузовых вагонов:
— порожние четырехосные на роликовых подшипниках при осевой нагрузке g ≤ 6 т/ось
|
Wо |
= |
1.0 |
+ |
0.044*V |
+ |
0.00024*V2 |
( 1.21 ) |
— груженые четырехосные на роликовых подшипниках при осевой нагрузке g > 6 т/ось
|
Wо |
= 0.7 + |
3 + 0.1*V + 0.00025*V2 |
|
|
|
|
( 1.22 ) |
|
g |
|
|
|
|
Для остальных видов вагонов расчетные формулы приведены в Правилах тяговых расчетов для поездной работы (ПТР).
Величина сопротивления от пути ic подставляется в формулы в виде суммарного значения сопротивления от уклона элементов профиля пути с учетом сопротивления от кривой на участке, равном длине поезда плюс ожидаемая длина тормозного пути
|
iс |
= |
i1*l1 + i2*l2 + i3*l3 + …. + in*ln |
, |
|
|
|
( 1.23 ) |
|
L + Sт |
|
|
|
где:
i – значения уклонов элементов профиля пути, ‰;
l – длина элементов профиля пути, м;
L – длина поезда, м;
S – ожидаемый тормозной путь, м.
Пример. Имеется некоторый участок пути со следующим профилем
Спрямленный уклон для этого участка пути составит:
|
iс |
= |
3*150+4*300-1.5*400-2*350+5*250+2.5*150 |
= |
0.7 |
|
|
|
|
|
150+300+400+350+250+150 |
|
|
|
|
||||
Результаты расчетов тормозного пути сводятся в табл. 1.3.
Таблица 1.3.
|
Vн |
Vк |
Vср |
Ψ |
bт |
Wox |
iс |
Sд |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Действительный тормозной путь при автостопном торможении определяется так же, как при экстренном торможении, а время подготовки тормозов к действию рассчитывают с учетом дополнительных 12 секунд необходимых для срабатывания ЭПК автостопа.
По этой методике можно рассчитать тормозной путь любого поезда при полных торможениях.
Сайт управляется системой uCozРАСЧЕТ ТОРМОЗНОГО ПУТИ ЭЛЕКТРОПОЕЗДОВ ПРИ ЭКСТРЕННОМ ТОРМОЖЕНИИ Текст научной статьи по специальности «Механика и машиностроение»
УДК 629.4.017 ГРНТИ 73.29.17
РАСЧЕТ ТОРМОЗНОГО ПУТИ ЭЛЕКТРОПОЕЗДОВ ПРИ ЭКСТРЕННОМ ТОРМОЖЕНИИ
Миронов Дмитрий Олегович
Соискатель,
ФГАОУ ВО «Российский университет транспорта (МИИТ»,
г. Москва, ул. Образцова, д. 9.
АННОТАЦИЯ
Целью исследования является определение эффективности тормозной системы электропоезда через расчет длины его тормозного пути при экстренном торможении. Использованы общелогические методы и методы математического моделирования. В результате получены значения длины тормозного пути для отдельных вагонов электропоезда ЭП2Д и для 10-вагонного электропоезда ЭП2Д с типовой тормозной системой с колодочным тормозом и с измененной тормозной системой с дисковым тормозом. Расчеты выполнены для подвижного состава без учета веса пассажиров и переменных пассажиропотоков (учитывалась только тара вагонов). Установлено, что применение дискового тормоза вместо колодочного способствует существенному сокращению длины тормозного пути, в частности, на мотор-вагонном подвижном составе с противоюзной системой благодаря большему коэффициенту трения композиционных тормозных накладок по сравнению с чугунными тормозными колодками.
ABSTRACT
The purpose of the study is to determine the effectiveness of the braking system of an electric train by calculating the length of its braking distance during emergency braking. General logical methods and methods of mathematical modeling are used. As a result, the values of the braking distance for individual cars of the EP2D electric train and for a 10-car EP2D electric train with a standard brake system with a pad brake and a modified brake system with a disc brake are obtained. The calculations were made for rolling stock without taking into account the weight of passengers and variable passenger flows (only the container of cars was taken into account). The use of disc brakes instead of drum greatly reduces the stopping distance, in particular, motor-wagon rolling stock with antiskid system due to the greater coefficient of friction of composite brake lining compared with cast iron brake blocks.
Ключевые слова: электропоезд, экстренное торможение, фрикционный тормоз, длина тормозного пути, дисковый тормоз.
Keywords: electric train, emergency braking, friction brake, brake path length, disc brake.
На скоростных электропоездах применяется автоматический пневматический фрикционный дисковый тормоз, который является резервным и, как правило, используется только для полной остановки электропоезда. В междугородном и пригородном сообщении используются и электропоезда городского типа такие, как ЭП2Д [3], которые часто эксплуатируются в качестве экспрессов. Такие электропоезда имеют автоматический пневматический фрикционный колодочный тормоз, выполненный по стандартной для отечественных электропоездов схеме. На скоростных пассажирских вагонах дисковый тормоз стал уже привычным, типовым, а на отечественном мотор-вагонном подвижном составе, рассчитанном на скорости эксплуатации до 120 км/ч, применяется колодочный тормоз. При экстренном торможении для быстрой остановки транспортного средства одновременно применяются все имеющиеся тормозные системы, для фрикционного тормоза экстренное торможение означает максимально возможное давление сжатого воздуха в тормозных цилиндрах и максимально возможное нажатие тормозных колодок (накладок) на ось, что вызывает повышенный нагрев в парах трения фрикционного тормоза.
Эффективность фрикционного тормоза зависит от множества параметров, которые изменяются во времени нелинейно (нажатие колодок (накладок), коэффициент трения, коэффициент сцепления). Подвижной состав с дисковым тормозом обязательно оснащается противоюзной системой, что предотвращает заклинивание колесных пар и существенное снижение тормозного эффекта.
Известно, что скоростной мотор-вагонный подвижной состав типа ЭС-2Г «Ласточка» [4] имеет по два тормозных диска на колесных парах моторных вагонов (с тяговыми
электродвигателями) и по три тормозных диска на колесных парах прицепных вагонов (без тяговых электродвигателей). Однако имеется ограничение по суммарному нажатию тормозных накладок на ось, соответственно, под разными вагонами (моторными и прицепными) максимальные давления сжатого воздуха в тормозных блоках различны.
Также в эксплуатации находятся электропоезда типа ЭГ-2Тв «Иволга» [2], которые имеют по 4 тормозных блока фирмы Knorr-Bremse и по 4 тормозных диска на каждой тележке (по 2 на каждой колесной паре), в отличие от электропоездов типа «Ласточка», у которых разное
количество тормозных блоков и тормозных дисков под вагонами разного типа.•(Ьт + ш0 + icy
где Ук — конечная скорость вагона, км/ч; 4 — замедление экипажа, км/ч; Ьт — удельная тормозная сила, Н/кН;
Результаты расчета длины тормозного
Юо — основное удельное сопротивление движению вагона, Н/кН;
ь — удельное ускоряющее усилие на поезд от уклона пути.
Удельная тормозная сила является функцией нажатия тормозных колодок (накладок) и коэффициента трения. Важным условием выбора нажатия тормозных колодок или накладок является недопущение юза. Подвижной состав с дисковым тормозом в обязательном порядке оснащается противоюзной системой в отличие от подвижного состава с колодочным тормозом. При использовании колодочного тормоза возможное нажатие тормозных колодок не используется полностью, т.к. может привести к заклиниванию колесных пар при торможении. Одним из преимуществ дискового тормоза является более эффективное использование нажатия тормозных накладок.
Для примера был выполнен расчет длины тормозного пути отечественного электропоезда ЭП2Д без ограничения нажатия тормозных колодок и с ограничением нажатия из условия недопущения юза. Результаты расчета представлены в таблице 1 и на рисунке 1.
Таблица 1.
№ п/п Тип вагона (поезда) Длина тормозного пути, м
Без учета юза С учетом юза
1 Головной вагон 388,9 769,3
2 Моторный вагон 455,9 797,2
3 Немоторный вагон 378,8 760,4
4 10-вагонный поезд 421,8 782
Как видно из таблицы 1, при выполнении условия недопущения юза длина тормозного пути значительно увеличивается из-за ограничения нажатия тормозных колодок. Далее был выполнен расчет длины тормозного пути электропоезда
ЭП2Д с пассажирами (по 100 человек в каждом моторном и немоторном вагонах и по 60 человек в каждом головном вагоне), результаты расчета представлены в таблице 2.
800
790
г? 780
о
8 770
S о. о
гс 760
5
750
740
Головной вагон Моторный вагон Немоторный вагон 10-вагонный поезд
Рисунок 1. Длина тормозного пути электропоезда ЭП2Д без пассажиров
Таблица 2.
Результаты расчета длины тормозного _ пути электропоезда ЭП2Д с пассажирами
№ п/п Тип вагона (поезда) Количество пассажиров Длина тормозного пути, м
1 Головной вагон 60 850,4
2 Моторный вагон 100 908,5
3 Немоторный вагон 100 907,5
4 10-вагонный поезд 920 896,9
При применении на электропоезде ЭП2Д дискового тормоза с противоюзным устройством можно получить больший тормозной эффект, за счет лучшего использования нажатия тормозных накладок. Применение дискового тормоза с тормозными блоками способствует снижению подготовительного тормозного пути, т.к. объем пневмоцилиндров тормозных блоков гораздо
Результаты расчета длины тормозного
меньше объема тормозных цилиндров, больше КПД механической части тормоза и быстрее устанавливается максимальное давление сжатого воздуха в них.
Был выполнен расчет длины тормозного пути электропоезда ЭП2Д без пассажиров с дисковым тормозом, результаты расчета представлены в таблице 3.
Таблица 3.
пути электропоезда ЭП2Д без пассажиров_
№ п/п
Тип вагона (поезда)
Длина тормозного _пути, м_
с колодочным тормозом
с дисковым тормозом
1
Головной вагон
769,3
662,3
Моторный вагон
797,2
655,9
Немоторный вагон
760,4
622
10-вагонный поезд
782
647,8
2
3
4
Из таблицы 3 видно, что дисковый тормоз более эффективен, чем колодочный, т.к. в нем более эффективно используется нажатие тормозных накладок. При увеличении коэффициента сцепления колес с рельсами при экстренном торможении (например, подача песка под колеса) появляется возможность лучшего использования нажатия тормозных блоков, что также приводит к сокращению длины тормозного пути.
ВЫВОДЫ.
Применение в тормозной системе противоюзного устройства способствует лучшему использованию нажатия тормозных колодок (накладок), что способствует уменьшению
тормозного пути. Дисковый тормоз имеет ряд преимуществ перед колодочным. При увеличении веса подвижного состава увеличивается длина тормозного пути.
Список литературы:
1 Асадченко В.Р. Расчет пневматических тормозов железнодорожного подвижного состава / Асадченко В.Р. // Учебное пособие для вузов ж.-д. транспорта. — М.: Маршрут, 2004. — 120 с.
2 http://www.tvz.ru/catalog/emus/
3 http ://www.dmzavod. ru/products/elektropoezd-postoyannogo-toka-ep2d/
4 https://ulkm.ru/produkciya/elektropoezd-lastochka/
10.3. Тормозные расчеты с помощью номограмм
Чтобы облегчить тормозные расчеты, специалисты ВНИИЖТа разработали номограммы — графики, связывающие тормозные пути при экстренном торможении с расчетными тормозными коэффициентами и со скоростями движения в начале торможения. Такие номограммы выполнены для разных уклонов и приведены в ПТР для площадок и спусков через 2 %о для грузовых и пассажирских поездов.
На рис. 10.6 приведен график sT(dp) при скоростях движения от 30 до 120 км/ч для грузового поезда на горизонтальном прямолинейном пути (i = 0).
Для определения тормозного пути с начальной скорости, например 90 км/ч при др = 0,4, находим точку А пересечения кривой sT($p) при V = 90 км/ч с вертикальной линией, соответствующей йр = 0,4 (40 кН на 100 кН веса поезда). Сносим эту точку на ось ординат и получаем тормозной путь 900 м (при I = 0). Если необходимо определить тормозной путь при снижении скорости, например, от 90 до 60 км/ч, находим дополнительно точку на кривой sT($p) при V = 60 км/ч (точка В). Тормозной путь при снижении скорости от 90 до 60 км/ч будет равен разности ординат точек А и В (900 — 405 = 495 м).
Эту номограмму можно использовать и для определения необходимого расчетного тормозного коэффициента, при котором поезд можно было остановить с заданной скорости в пределах заданного тормозного пути . Например, чтобы остановить грузовой поезд на горизонтальном прямолинейном пути со скорости 90 км/ч в пределах тормозного пути 1000 м, находим точку пересечения кривой, соответствующей скорости 90 км/ч, с горизонтальной линией при 5Т = 1000 м (точка С). Получаем: Фр = 35 кН на 100 кН веса состава (или Ф = 0,35).
Чтобы определить sT или Jp на спусках, необходимо использовать соответствующую номограмму из ПТР. Наибольшую скорость на горизонтальном прямолинейном пути находят по заданному тормозному пути и расчетному тормозному коэффициенту. Например, при sT = 900 м и Фр = 0,3 (точка D) Допустимая скорость одоп = 80 км/ч. Если точка оказывается между кривыми скорости, то ее находят методом интерполяций.
Рис. 10.6. Номограмма для тормозных расчетов грузового поезда при i = 0
На рис. 10.7 показаны номограммы для экстренного тор-
Рис. 10.7. Номограмма для тормозных расчетов пассажирского поезда на спуске 10 %о при электропневматическом (сплошные линии) и пневматическом (штриховые) торможении
Можения пассажирского поезда на спуске 10 %0 при использовании электропневматического (сплошные линии) и пневматического (штриховые линии) тормозов. Из них видно, что тормозные пути при одинаковых скоростях движения и одинаковых Фр при электро-пневматических тормозах меньше, чем при пневматических. Так, при V = 100 км/ч и $р = 0,6 тормозные пути sT составляют 805
И 870 м (точки А и В). При одном и том же тормозном пути
Расчетный тормозной коэффициент Фр при пневматических тормозах должен быть больше. При V = 100 км/ч и sT = 800 м Фр соответственно равен 0,6 и 0,66 (точки А и С).
Имея набор номограмм, можно находить результаты тормозных расчетов без выполнения самих расчетов.
% PDF-1.4 % 274 0 объект > эндобдж xref 274 144 0000000016 00000 н. 0000003232 00000 н. 0000003414 00000 н. 0000003478 00000 н. 0000004379 00000 н. 0000004597 00000 н. 0000004681 00000 п. 0000004849 00000 н. 0000005046 00000 н. 0000005248 00000 н. 0000005309 00000 н. 0000005440 00000 н. 0000005576 00000 н. 0000005637 00000 п. 0000005777 00000 н. 0000005838 00000 н. 0000006029 00000 н. 0000006090 00000 н. 0000006243 00000 н. 0000006375 00000 н. 0000006520 00000 н. 0000006581 00000 н. 0000006744 00000 н. 0000006805 00000 н. 0000006955 00000 н. 0000007016 00000 н. 0000007077 00000 н. 0000007138 00000 н. 0000007281 00000 п. 0000007342 00000 п. 0000007403 00000 н. 0000007618 00000 н. 0000007678 00000 н. 0000007809 00000 н. 0000007935 00000 п. 0000007996 00000 н. 0000008191 00000 п. 0000008252 00000 н. 0000008445 00000 н. 0000008583 00000 н. 0000008734 00000 н. 0000008795 00000 н. 0000008980 00000 н. 0000009041 00000 н. 0000009273 00000 н. 0000009334 00000 п. 0000009529 00000 н. 0000009590 00000 н. 0000009735 00000 н. 0000009796 00000 н. 0000009857 00000 н. 0000009918 00000 н. 0000010070 00000 п. 0000010209 00000 п. 0000010372 00000 п. 0000010433 00000 п. 0000010584 00000 п. 0000010645 00000 п. 0000010706 00000 п. 0000010767 00000 п. 0000010918 00000 п. 0000010978 00000 п. 0000011038 00000 п. 0000011129 00000 п. 0000011190 00000 п. 0000011321 00000 п. 0000011447 00000 п. 0000011507 00000 п. 0000011660 00000 п. 0000011720 00000 н. 0000011874 00000 п. 0000011934 00000 п. 0000012132 00000 п. 0000012192 00000 п. 0000012378 00000 п. 0000012503 00000 п. 0000012563 00000 п. 0000012623 00000 п. 0000012820 00000 п. 0000012945 00000 п. 0000013076 00000 п. 0000013136 00000 п. 0000013277 00000 п. 0000013337 00000 п. 0000013483 00000 п. 0000013543 00000 п. 0000013689 00000 п. 0000013749 00000 п. 0000013809 00000 п. 0000013869 00000 п. 0000014030 00000 п. 0000014170 00000 п. 0000014316 00000 п. 0000014376 00000 п. 0000014534 00000 п. 0000014594 00000 п. 0000014747 00000 п. 0000014807 00000 п. 0000014867 00000 п. 0000014927 00000 п. 0000015086 00000 п. 0000015146 00000 п. 0000015310 00000 п. 0000015369 00000 п. 0000015563 00000 п. 0000015624 00000 п. 0000015741 00000 п. 0000015800 00000 п. 0000015861 00000 п. 0000015974 00000 п. 0000016065 00000 п. 0000016175 00000 п. 0000016282 00000 п. 0000016385 00000 п. 0000016435 00000 п. 0000016485 00000 п. 0000016546 00000 п. 0000016701 00000 п. 0000016809 00000 п. 0000016918 00000 п. 0000018230 00000 п. 0000018253 00000 п. 0000019416 00000 п. 0000019439 00000 п. 0000020616 00000 п. 0000020639 00000 п. 0000021844 00000 п. 0000021867 00000 п. 0000021977 00000 п. 0000023137 00000 п. 0000023159 00000 п. 0000023402 00000 п. 0000023510 00000 п. 0000023614 00000 п. 0000024613 00000 п. 0000024635 00000 п. 0000025689 00000 п. 0000025712 00000 п. 0000026833 00000 п. 0000026855 00000 п. 0000026932 00000 п. 0000027063 00000 п. 0000003551 00000 н. 0000004357 00000 н. трейлер ] >> startxref 0 %% EOF 275 0 объект > эндобдж 276 0 объект > эндобдж 277 0 объект > эндобдж 416 0 объект > ручей HR_HSQ \ $ E0ĚQQYcICwWzph) f« {+ 7_% D_ «lH (A˦`} \
Поезд Измерения и расчеты тормозного пути: factorio
Привет,
В рамках моего проекта LTN в Vanilla я хочу поезда чтобы иметь возможность поддерживать полную скорость на перекрестках, а это значит, что я должен был иметь возможность определять, сколько плиток нужно, чтобы поезд остановился на полной скорости.Я пытался выяснить, измерял ли кто-нибудь тормозной путь раньше, но я не заметил, чтобы кто-нибудь измерил (может, мой гугл-фу меня не подводит), поэтому я сделал это сам.
Используемый метод:
Установите длинную петлю рельса
Установите сигналы как можно ближе друг к другу вдоль одного края петли и свяжите их вместе зеленым проводом. Все настроены на отчетный цвет сигнала.
Привяжите выход к опоре. Наведите указатель мыши на столб во время проезда поезда, чтобы увидеть, сколько сигналов желтого цвета.
Используйте максимальное количество желтых сигналов * 2 в качестве тормозного пути поезда.
Вот как это выглядит (обратите внимание на количество желтых сигналов на информации о полюсе питания).
При этом обнаружил некоторые интересные вещи:
Локомотивы применяют одинаковую силу торможения независимо от типа топлива (зависит только от исследования тормозной силы) или даже от топлива вообще (локомотивы без топлива тормозят так же сильно, как и локомотивы, работающие на топливе. ). Поезда, работающие на угле, останавливаются на меньшем количестве плиток, чем поезда, работающие на урановом топливе, но это потому, что их максимальная скорость ниже, а не из-за разницы тормозных сил.
Локомотивы применяют одинаковую тормозную силу при движении вперед или назад
Вагоны Применяют некоторое тормозное усилие, но не такое большое, как у локомотивов
Грузовые вагоны и вагоны с жидкостью применяют одинаковое тормозное усилие.
Артиллерийские вагоны применяют примерно такое же тормозное усилие, как и обычные вагоны, но весят в 4 раза больше, поэтому поездам, содержащим их, требуется значительно больше времени для замедления с тем же соотношением двигателей / вагонов, что и у обычного поезда такой длины.
Испытания были проведены со всеми завершенными исследованиями тормозной силы с поездами, работающими на урановом топливе (за исключением нескольких испытаний с углем, чтобы увидеть, имеет ли значение тип топлива):
| Тип топлива | # Конфигурация поезда | Итого Масса | Макс. Желтый Сигналы | Дистанция остановки в плитках (сигналы * 2) |
|---|---|---|---|---|
| Уголь | 1-0 | 2000 | 37 | 74 |
| Атомная промышленность | 1-0 | 2000 | 48 | 96 |
| 2-0 | 4000 | 48 | 96
| 1-0-1 | 4000 | 48 | 96
| 1-0-2 | 6000 | 48 | 96
| 1-1 | 3000 | 54 | 108
| 1-2 | 4000 | 58 | 116
| 1-3 | 5000 | 61 | 122
| 1-4 | 6000 | 63 | 126
| 1-5 | 7000 | 64 | 128
| 1-6 | 8000 | 66 | 132
| 2-4 | 8000 | 58 | 116
| 1-1 (Артиллерийский вагон) | 6000 | 107 | 214
| 1-2-1 | 6000 | 54 | 108
Исходя из этого, я смог рассчитать среднюю тормозную силу каждого поезда, используя уравнения кинетической энергии:
E = 0.5 м v 2
E = F * d
F d = 0,5 м * v 2
F = 0,5 м v 2 / d
Используя приведенный выше расчет силы (и предполагая, что масса поезда выражена в кг и 1 плитка = 1 метр), я смог определить следующее:
Затем вы можете использовать приведенную ниже формулу для расчета тормозного пути для произвольного настроил поезд. Это не совсем идеально, но дает результаты в пределах 1-2 плиток от измеренного расстояния, так что, вероятно, есть какое-то отношение к сопротивлению воздуха, которое я не принимаю во внимание при вычислении.
d = 0,5 * Общая масса * (максимальная скорость * 1000/3600) 2 / ((Кол-во локомотивов * 71000) + (Кол-во вагонов * 23000))
Максимальная скорость для поездов, работающих на урановом топливе, составляет 298,1 км / ч.
Максимальные скорости для различных других конфигураций поездов и типов топлива можно найти здесь.
Выводы из этого относительно размера поезда и размера блока:
Предположим следующее:
Вы хотите, чтобы ваши поезда могли останавливаться с полной скорости в пределах одного сигнального блока.
Вы хотите достаточно эффективно использовать эти сигнальные блоки, создав поезда, которые их полностью заполняют.
Вы хотите сохранить соотношение 1-2 локомотив-вагон (для максимального ускорения) или 1-2-1 для двухсторонних поездов.
Это дает нам:
Для остановки поездов с соотношением 1-2 требуется 116 плиток. Поезда 6-12 имеют длину 125 плиток и являются наименьшим размером, который следует использовать для полного заполнения блока, в котором поезд может остановиться с полной скорости.
Поезда 5-10 имеют длину 104 плитки и, следовательно, заполняют 89,6% блока из 116 плиток, если вам нужен минимальный размер блока для полной остановки и вы готовы принять некоторую потерянную площадь.
Для остановки поездов с соотношением 1-2-1 требуется 108 плиток. Поезда 4-8-4 имеют длину 111 клеток и являются наименьшим размером, который следует использовать для полного заполнения блока, в котором поезд может остановиться с полной скорости.
Учитывая, что длина поезда и расстояние между остановками так близки, кажется глупым не использовать только поезд такого размера.
Я не уверен, есть ли в этом какие-то преимущества, помимо того, что я пытаюсь сделать с моей схемной сетью, управляемой маршрутизацией поездов, но, надеюсь, кто-то еще сочтет это полезным. Спасибо за чтение :).
TL; DR : Поезда идут на определенное расстояние до остановки, я выяснил, какое расстояние для разных конфигураций поездов. Используйте как хотите.
Расчет расстояния и сигнализация тормозного пути для размещения сигналов железной дороги
Расчет расстояния и сигнализация тормозного пути для размещения сигналов железной дороги, ПРОЕЗДА ДЛЯ НЕОСТАНАВЛИВАЮЩИХСЯ ПОЕЗДОВ, ПРОЕЗДА — ИЗМЕРЕНИЕ ЧАСТОГО ПЕРЕДАЧИ ПОЕЗДОВ, РАСЧЕТ ПРОЕЗДА ПРОЕЗДА, РЕЗЮМЕ ПРОЦЕССА РАСЧЕТА ПРОЦЕССА ПЕРЕДАЧИ ПЕРЕДАЧ, ПРОЦЕСС РАССТОЯНИЕ, РАСЧЕТНОЕ ТОРМОЗНОЕ РАССТОЯНИЕ СИГНАЛА, ОБЗОРНОЕ РАССТОЯНИЕ И РАССТОЯНИЕ СЧИТЫВАНИЯ, пояснения по железнодорожным сигналам, железнодорожные сигналы в формате pdf, принцип работы железнодорожных сигналов, британские железнодорожные сигналы, типы железнодорожных сигналов ppt, железнодорожные сигналы в формате PDF на хинди, 4-сторонняя сигнализация, объяснение сигналов поездов
ПРОЕЗДА БЕЗОПАСНЫХ ПОЕЗДОВ
* РАСЧЕТ ПРОЕЗДА — НЕОБХОДИМЫЙ ПЕРВЫЙ ШАГ ПРИ СИГНАЛИЗАЦИИ ПЛАНА
Он обеспечивает лучшее инженерное решение, которое отвечает противоречивым требованиям по эксплуатационной мощности, безопасности и стоимости.
* ПРОЕЗДА — ИЗМЕРЕНИЕ ЧАСТОТЫ ПЕРЕДАЧИ ПОЕЗДОВ.
ОНА ОЧЕНЬ (установлена расчетом) В ФОРМЕ
(i) ВРЕМЯ ПРОЕЗДА ИЛИ (ii) РАССТОЯНИЕ ПРОЕЗДА
* «ВРЕМЯ ПРОЕЗДА» (HT) — ВРЕМЯ, ЗАДАВАЕМОЕ СЛЕДУЮЩИМ ПОЕЗДОМ, ЧТОБЫ ПРОЕХАТЬ ЗАДАННУЮ ТОЧКУ НА ПОЛНОЙ СКОРОСТИ ПОСЛЕ ПРЕДЫДУЩИХ ПОЕЗДОВ, ПРОЕЗДАЮЩИХ ЕЕ, С учетом МИНИМАЛЬНОГО РАЗДЕЛЕНИЯ, РАЗРЕШЕННОГО СИСТЕМОЙ СИГНАЛИЗАЦИИ.
* «ПРОЕЗДНОЕ РАССТОЯНИЕ» (HD) — РАССТОЯНИЕ МЕЖДУ ДВУМ ПОСЛЕДОВАТЕЛЬНЫМИ ПОЕЗДАМИ, ПРОДОЛЖАЮЩИМ ОДНУ ТОЧКУ СО СЛЕДУЮЩИМ ПОЕЗДОМ НА ПОЛНОЙ СКОРОСТИ В СООТВЕТСТВИИ С МАКСИМАЛЬНОЙ ЧАСТОТОЙ, РАЗРЕШЕННОЙ СИСТЕМОЙ СИГНАЛИЗАЦИИ.
РАСЧЕТ ПРОДОЛЬНОГО РАССТОЯНИЯЦЕЛЬ РАСЧЕТА ПРОЕЗД — ОПРЕДЕЛИТЬ, КАКОЙ ТИП СИГНАЛИЗАЦИИ, С КАКИМ РАЗДЕЛЕНИЕМ СИГНАЛОВ НЕОБХОДИМО, ЧТОБЫ СООТВЕТСТВОВАТЬ СПЕЦИФИКАЦИИ КЛИЕНТА САМЫМ ЭКОНОМИЧНЫМ СПОСОБОМ.
РЕЗЮМЕ ПРОЦЕССА РАСЧЕТОВ:
1. ОПРЕДЕЛЯЕТ САМЫЕ ИНТЕНСИВНЫЕ СЛУЖБЫ ПОЕЗДОВ, КОТОРЫЕ ОБЯЗАНЫ ВЫПОЛНЯТЬ «РАСЧЕТ ПРОЕЗДА» ДЛЯ КАЖДОЙ ЛИНИИ.
2. РАССЧИТАТЬ «СКОРОСТЬ ОБСЛУЖИВАНИЯ» В « м / сек »
3. РАССЧИТАТЬ « ПРОДОЛЖИТЕЛЬНОСТЬ ПРОДОЛЖИТЕЛЬНОСТИ» (HD) ДЛЯ ЛИНИИ (HT x V)
4. ВЫЧИТАЙТЕ «РАССТОЯНИЕ ОТ ЗЕЛЕНОГО ДО КРАСНОГО» (DGR = HD-R-O-L, ГДЕ «R» — РАССТОЯНИЕ СЧИТЫВАНИЯ СИГНАЛА »,« O »- ПЕРЕСЕЧЕНИЕ СИГНАЛА,« L »- МАКСИМАЛЬНАЯ ДЛИНА ПОЕЗДА)
5. ВЫЧИТАЙТЕ ОТНОШЕНИЕ «РАССТОЯНИЯ ОТ ЗЕЛЕНОГО К КРАСНОМУ» К РАССТОЯНИЮ СИГНАЛА ТОРМОЖЕНИЯ (N = DGR / SBD)
НА ОСНОВЕ ДАННОГО РАСЧЕТА «N» И ВОЗМОЖНОГО «ДИАПАЗОНА РАЗДЕЛЕНИЯ СИГНАЛОВ» ВЫБЕРИТЕ ТИП ПРЕДОСТАВЛЯЕМОЙ СИГНАЛЬНОЙ СИСТЕМЫ.
ПРОСТРАНСТВО МЕЖДУ ПОСЛЕДОВАТЕЛЬНЫМИ СИГНАЛАМИ ОСТАНОВА
* НЕОБХОДИМО ПРОСТРАНСТВО МЕЖДУ ПОСЛЕДОВАТЕЛЬНЫМИ СИГНАЛАМИ ОСТАНОВА «D» —
КАК «D2» В 2-х АСПЕКТНЫХ СИГНАЛЬНЫХ ТЕРРИТОРИЯХ,
КАК «D3» НА ТРЕХ АСПЕКТНЫХ СИГНАЛЬНЫХ ТЕРРИТОРИЯХ &
КАК «D4» НА 4 АСПЕКТНЫХ СИГНАЛЬНЫХ ТЕРРИТОРИЯХ.
* ПАРАМЕТРЫ, РАССМАТРИВАЕМЫЕ ДЛЯ РАСЧЕТА РАССТОЯНИЯ СИГНАЛА:
(1) ВРЕМЯ ПРОЕЗДА В СЕКУНДАХ (HT), (2) РАССТОЯНИЕ ПРОЕЗДА В МЕТРАХ
(3) СКОРОСТЬ ОБСЛУЖИВАНИЯ ПОЕЗДА (V) В МЕТРАХ В СЕКУНДУ (м / с) БУДЕТ ПРЕОБРАЗОВАТЬСЯ ИЗ ПРЕДОСТАВЛЕННЫХ МИЛЬ В ЧАС (М / Ч).
* НЕОБХОДИМОЕ ПРОСТРАНСТВО МЕЖДУ СИГНАЛАМИ ВЫЧИСЛЯЕТСЯ С ПОМОЩЬЮ ФОРМУЛЫ: D = V * HT (СКОРОСТЬ x ВРЕМЯ) МАКСИМАЛЬНАЯ СКОРОСТЬ И ВРЕМЯ ПРОЕЗДА, ОБЕ УКАЗЫВАЕТСЯ КЛИЕНТОМ ПО ТРЕБОВАНИЮ.
* ТАКЖЕ НАЗЫВАЕТСЯ «СЕРВИСНОЕ ТОРМОЗНОЕ РАССТОЯНИЕ» (SBD), ЭТО РАЗРЕШЕННЫЙ МИНИМАЛЬНЫЙ
РАССТОЯНИЕ НА ПОДХОДЕ К «КРАСНОМУ АСПЕКТУ» ОТ ПЕРВОГО СООТВЕТСТВУЮЩЕГО «ВНИМАНИЕ»
ASPECT («ЖЕЛТЫЙ» ИЛИ «ДВОЙНО-ЖЕЛТЫЙ», ПРИ ИСПОЛЬЗОВАНИИ).
* «SBD» ЗАВИСИТ ОТ:
(1) СМЕСЬ ВИДОВ ПОЕЗДОВ, ИСПОЛЬЗУЮЩИХ ЛИНИЮ (УКАЗАНО ЗАКАЗЧИКОМ)
У разных поездов разная тормозная способность (что еще хуже)
(1) МАКСИМАЛЬНАЯ ДОПУСТИМАЯ СКОРОСТЬ (ТАКЖЕ УКАЗАННАЯ ЗАКАЗЧИКОМ)
(2) РЕГУЛИРУЮЩИЙ ГРАДИЕНТ ПУТЕШЕСТВИЯ РАЗДЕЛА (ПО ИЗМЕРЕНИЮ ИЛИ УКАЗАННОМ КЛИЕНТОМ)
«SBD» ПРЕДОСТАВЛЯЕТСЯ В ТАБЛИЦЕ ОБЗОРА В СТАНДАРТАХ ЖЕЛЕЗНОДОРОЖНОЙ ГРУППЫ ДЛЯ СПРАВОЧНИКА
СИГНАЛИЗАЦИЯ ТОРМОЗНОЙ РАССТОЯНИЯ (ручной расчет)
РАСЧЕТНАЯ СИГНАЛЬНАЯ ДИСТАНЦИЯ ТОРМОЖЕНИЯ
* ЗАВИСИТ ОТ ТОРМОЗНОЙ МОЩНОСТИ ПОЕЗДА, «a» В ЕДИНИЦАХ: «м в секунду в секунду» (м / с2).
ЕГО ТИПИЧНОЕ ЗНАЧЕНИЕ = 0,5 м / с2
SBD, S = U2 / 2a, ГДЕ «U» — МАКСИМАЛЬНАЯ СКОРОСТЬ ПОЕЗДА, а «a» — ТОРМОЗНАЯ МОЩНОСТЬ ПОЕЗДА.
(Сигнальное расстояние торможения (S) прямо пропорционально требуемой максимальной скорости поезда и обратно пропорционально доступной тормозной способности поезда, как указано клиентом).
* ДЛЯ РАСЧЕТА «SBD» ДЛЯ СКОРОСТИ ПОЕЗДА 100 МИЛЬ В ЧАС:
(a) сначала преобразуйте единицы скорости из миль в час в «м / с». 100 миль в час = 100 x (1609/3600) = 44.7 м / с.
(b), тогда S = (44,7) 2 / 2a = (44,7) 2/2 x 0,5 = 1998m.
ТОРМОЗНОЕ РАССТОЯНИЕ с использованием ТАБЛИЦЫ LOOK UP Среднее значение Градиент
SBD (MIN) КАК УКАЗАНО В ТАБЛИЦЕ ПРОСМОТРА
* «SBD» ТАКЖЕ ВЫЧИСЛЯЕТСЯ НА ОСНОВЕ ДОСТУПНЫХ ДАННЫХ, ВКЛЮЧАЯ «ТОРМОЗНАЯ СПОСОБНОСТЬ ПОЕЗДА» ДЛЯ ОПРЕДЕЛЕНИЯ МАКСИМАЛЬНОГО ПРОСТРАНСТВА, КОТОРОЕ СЧИТАЕТСЯ СОХРАНЯЕМЫМ МЕЖДУ ЗНАКОМ «ПЕРВОЕ ПРЕДУПРЕЖДЕНИЕ» И «КРАСНЫЙ АСПЕКТ» НА ПРАВИЛЬНОМ ПОЛОЖЕНИИ 9025.
ПРИЗОРНАЯ ДИСТАНЦИЯ И ДИСТАНЦИЯ СЧИТЫВАНИЯ
* «Прицельная дистанция» ИНОГДА НАЗЫВАЕТСЯ РАССТОЯНИЕМ МЕЖДУ САМОЙ РАННЕЙ ТОЧКОЙ ПОСАДКИ, НА КОТОРОЙ ПОЛУЧАЕТСЯ СИГНАЛ, И СИГНАЛОМ.
*, НО В большинстве случаев ЭТО ПРИНИМАЕТСЯ В КАЧЕСТВЕ «ПОСЛЕДНЕГО ПЕРИОДА НЕПРЕРЫВНОГО ВИДЕНИЯ» НА ЗАКЛЮЧИТЕЛЬНОМ ПОДХОДЕ К СИГНАЛУ, КОТОРЫЙ КАЖЕТСЯ БОЛЕЕ ТОЧНЫМ.
* «РАССТОЯНИЕ СЧИТЫВАНИЯ» ПРИЗНАЕТСЯ БЕЗ ДАННОЙ НЕПОСРЕДСТВЕННОЙ ДАЛЬНОСТИ КАК ПОСЛЕДНЕЕ ОПРЕДЕЛЕННОЕ ПРИЗОРНОЕ РАССТОЯНИЕ, КОТОРОЕ ПРОДОЛЖАЕТСЯ В течение определенного периода.
* СТАНДАРТ ГРУППЫ GE / RT8037 ТРЕБУЕТ, ЧТО «КАЖДЫЙ СИГНАЛ, НАХОДЯЩИЙСЯ НА СКОРОСТИ, ЯВЛЯЕТСЯ НЕПРЕРЫВНЫМ В ТЕЧЕНИЕ АБСОЛЮТНОГО МИНИМУМА 8 СЕКУНД НА КОНЕЧНОМ ПОДХОДЕ К СИГНАЛУ , ДЛЯ ПОЕЗДА ПРИ МАКСИМАЛЬНО РАЗРЕШЕННОЙ СКОРОСТИ
».* НАСТОЯЩАЯ ПОСТОЯННАЯ МИНИМАЛЬНАЯ ВИДИМОСТЬ ОБЕСПЕЧИВАЕТ, ЧТО ВОДИТЕЛЬ МОЖЕТ РЕАГИРОВАТЬ НА МЕНЬШЕ РАЗРЕШИТЕЛЬНЫЕ / БОЛЕЕ ОГРАНИЧИТЕЛЬНЫЕ АСПЕКТЫ, СОБЛЮДАЕМЫЕ ПРИ НАЖАТИЕ ТОРМОЗОВ, БЕЗ ПОТЕРЯ БОЛЬШОГО ВРЕМЕНИ (ВКЛЮЧАЯ РАССТОЯНИЕ РЕАКЦИИ).
* СИГНАЛ МОЖЕТ БЫТЬ ВИДИМ НА ДАЛЬНЕМ РАССТОЯНИИ НА ПОДХОДЕ.ТОЛЬКО ТОРМОЖЕНИЕ (ДАЖЕ ДЛЯ НАИХИХ ПОЕЗДОВ) НЕОБХОДИМО НАЧАТЬ ПОСЛЕ ПЕРВОГО СИГНАЛА «ВНИМАНИЕ!
РАССТОЯНИЕ СЧИТЫВАНИЯ, РАССМОТРЕННОЕ НА ПРАКТИКЕ
* ЕСЛИ ПОЕЗД ДВИГАЕТСЯ ДО ПРЕДЕЛА ПРОМЫШЛЕННОСТИ ЛИНИИ, НАЧАЛЬНЫЙ АСПЕКТ СИГНАЛА ПРЕДОСТЕРЕЖЕНИЯ МОЖЕТ СОБЛЮДАТЬСЯ ДО ЗЕЛЕНОГО ЗЕЛЕНОГО ИЗ-ЗА того, что поезд EARLIR очищает свой участок и движется вперед до минимума 8 секунд.
* БОЛЕЕ ПРАКТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ РАССТОЯНИЯ ЧТЕНИЯ, МИНИМУМ 10 СЕКУНД ВРЕМЕНИ ЧТЕНИЯ СЧИТАЕТСЯ ПРАКТИЧЕСКИМ ОПРЕДЕЛЕНИЕМ РАСЧЕТА ПРОЕЗДА.
* ТАК КАК СИГНАЛЫ ПРЕДОСТАВЛЯЮТСЯ С «AWS», РАССТОЯНИЕ СЧИТЫВАНИЯ ТАКЖЕ МОЖЕТ БЫТЬ ТАКОМ, КАК СОДЕЙСТВОВАТЬ УМЕНЬШЕНИЮ СИГНАЛЬНОГО АСПЕКТА ДО ЗЕЛЕНОГО ПЕРЕДАЧИ ПОЕЗДА, ПРОЕЗДАЮЩЕГО НА МАГНИТЕ AWS TRACK, ДЛЯ ВОДИТЕЛЯ, ЧТОБЫ СЛУШАТЬ ПРЕДУПРЕЖДАЮЩИЙ ЗЕЛЁНЫЙ СИГНАЛ .
* РАССТОЯНИЕ СЧИТЫВАНИЯ 300 м ПРАКТИЧНО РАССЧИТЫВАЕТСЯ ДЛЯ РАСЧЕТА ПРОЕЗДА, ПОТОМУ ЧТО СЧИТАЕТСЯ РЕАЛЬНЫМ ДЛЯ ДИАПАЗОНА СКОРОСТИ ОКОЛО 70 миль / ч (113 км / ч).
Моделирование экстренного торможения высокоскоростного поезда и онлайн-идентификация изменяющихся во времени параметров
Путем анализа механизма воздушного экстренного торможения высокоскоростного поезда создана дискретная модель экстренного торможения.Стремясь решить проблему, заключающуюся в том, что изменяющиеся во времени скрытые параметры нельзя наблюдать напрямую, предлагается максимизация математического ожидания на основе скользящего окна и идентифицируются ненаблюдаемые изменяющиеся во времени параметры торможения. Во-первых, выбираются положение и размер скользящего окна; затем максимизация ожидания на основе скользящего окна используется для идентификации параметра торможения; наконец, в сочетании с оптимизацией градиента получены оптимальные определения параметров аварийного торможения.Результаты моделирования показывают, что с помощью предложенного метода можно быстро и точно определить параметры тормоза. В условиях равномерного шума ошибки идентификации коэффициента трения и тормозного отношения составляют ± 0,0068 и ± 0,0349 соответственно, а максимальные относительные ошибки между идентификацией и истинными значениями составляют 2,4807% и 1,3154% соответственно, что может удовлетворить фактическим требованиям тормозная система. Проверяется эффективность и целесообразность предложенных модели и метода.
1. Введение
Будучи важной частью железнодорожной транспортной системы [1–3], высокоскоростной поезд играет важную роль в национальном экономическом развитии, культурном обмене и городском строительстве [4–6]. Большое внимание уделяется тормозным характеристикам тормозной системы поезда, что является важной частью обеспечения безопасной эксплуатации поезда. Особого внимания заслуживает экстренное торможение, последний барьер безопасности тормозной системы поезда. Точное динамическое моделирование — основа точного торможения.Посредством точной оценки рабочих параметров модели торможения в режиме реального времени можно получить состояние рабочих характеристик поезда в реальном времени, что в значительной степени обеспечивает безопасность движения и повышает эффективность движения [7–9]. Поэтому очень важно изучить моделирование аварийного торможения высокоскоростных поездов и онлайн-идентификацию изменяющихся во времени параметров.
В настоящее время достигнут значительный прогресс в исследованиях моделирования торможения высокоскоростных поездов. Принимая во внимание сопротивление трения, аэродинамическое сопротивление и собственные нелинейные характеристики торможения поездов, Сонг и др. Установили однокоординатную многочастичную модель торможения., который отражает сопротивление и переходные эффекты на поездах [10]. Интегрируя динамику системы поезда и динамику торможения, Сонг и др. Разработали многочастичную модель динамики торможения поезда, которая имеет практическую применимость для отражения неопределенностей линейных / нелинейных параметров поезда и возможных неисправностей торможения [11]. Чтобы эффективно использовать рекуперативную энергию тормозного поезда и снизить фактическое потребление энергии во время движения, Су и др. Предложили модель совместного управления торможением поезда., что может эффективно минимизировать фактическое потребление энергии [12]. Для решения проблемы отслеживания и управления положением и скоростью высокоскоростного поезда, соединенного сцепками, Сонг и Сонг предложили модель динамики упругого столкновения, отражающую нелинейное сцепление / торможение и неисправности движения асимметричных транспортных средств [13]. На основе исследования принципа торможения поезда EMU, модель тормозной системы EMU была предложена Го и Се в соответствии с передачей инструкций по торможению и выработкой тормозной мощности [14].
При оценке параметров моделирования поездов были проведены глубокие исследования. Для динамической модели высокоскоростного поезда обобщенная оценка взвешенных параметров была предложена Ван и др., А контроллер был разработан в соответствии с ошибкой оценки [15]. Zhang et al. установили альтернативную модель на основе нейронной сети для сложной структуры и множества параметров поездов [16]. На основе анализа состава и характеристик тормозной системы городского рельсового поезда и ее взаимодействия с водителем модель торможения, подходящая для разработки контроллера и определения параметров модели, была предложена Ю и Ченом [17].Чжун и др. построена система дискретного пространства состояний одночастичной модели высокоскоростного поезда. Стремясь к негауссовым характеристикам шума поезда, нелинейности модели поезда и неполной измеримости состояния поезда, была предложена оценка максимального правдоподобия, подходящая для нелинейной модели высокоскоростного поезда, и постоянные рабочие параметры поезда были оценены [18]. Путем анализа продольных динамических характеристик высокоскоростного поезда, сочетания фильтра частиц и байесовской апостериорной вероятности на основе критерия максимизации математического ожидания был предложен метод онлайн-оценки для изменяющихся во времени параметров продольной динамической модели высокоскоростного поезда [19] .
Вышеупомянутые исследования позволили добиться значительного прогресса в создании модели поезда и идентификации параметров. Тем не менее, предыдущие исследования в основном были сосредоточены на постоянных параметрах модели железнодорожной системы, только оценка состояния системы или постоянных параметров и использование автономной оценки в качестве основного метода. Однако из-за различий в характеристиках поезда, сложности условий движения и механического износа в динамической модели поезда должны быть неопределенные и изменяющиеся во времени параметры.Более того, только гауссов шум используется для моделирования влияния случайных факторов, таких как пешеходы, дорожные условия и погода, что неизбежно приводит к проблеме потери информации, приводящей к неточности модели поезда [20–22]. В связи с указанными выше проблемами модель экстренного торможения высокоскоростного поезда построена на основе анализа механизма экстренного торможения поезда. Ориентируясь на изменяющиеся во времени параметры скрытых переменных, которые трудно наблюдать в модели, предлагается онлайн-идентификация параметров скрытых переменных на основе скользящего окна и максимального ожидания, которое реализует получение в реальном времени динамических характеристик и рабочего состояния высокого уровня. -скоростной поезд.
2. Моделирование экстренного торможения для высокоскоростных поездов
Экстренное торможение — одно из наиболее важных устройств в тормозной системе высокоскоростного поезда. Когда происходят серьезные аварии или аварии, влияющие на безопасность поезда во время работы поезда, это последняя гарантия безопасности высокоскоростного поезда и пассажиров. Поэтому очень важно провести глубокие исследования по моделированию экстренного торможения высокоскоростных поездов. В этой статье торможение чистым воздухом рассматривается как единственный эффективный режим торможения для экстренного торможения поезда.Путем изучения тормозного механизма тормозного устройства проводится силовой анализ поезда при торможении. Ссылаясь на Правила по расчету тяги поездов , модель дискретного экстренного торможения высокоскоростного поезда определяется следующим образом: где и указывают тормозной путь и скорость движения поезда, соответственно, — местоположение поезда, — поезд Время выборки, представляет собой сумму качества поезда и качества вращения, представляет собой случайное влияние на скорость и смещение поезда, которое вызвано условиями пути, погодными условиями и другими факторами, используется для характеристики ошибок измерения и представляет собой тормозную силу поезд.На тормозную силу влияют не только параметры торможения поезда, но и сила сцепления между колесами и рельсами. Где — диаметр тормозного цилиндра, — давление воздуха в тормозном цилиндре, — эффективность трансмиссии фундаментного тормозного устройства, — коэффициент торможения, — радиус трения тормозного диска, — диаметр колеса, — общее количество тормозных колодок транспортного средства, и — коэффициент трения тормозного диска и коэффициент сцепления между колесом и рельсом, соответственно (значения их варьируются. со скоростью торможения), — осевая нагрузка поезда, — это ускорение свободного падения.
представляет собой базовое сопротивление движению поезда; она положительно коррелирует со скоростью поезда. Обычно он выражается следующим образом: где — коэффициент сопротивления качению, — другой коэффициент механического сопротивления, который пропорционален скорости поезда, и — коэффициент сопротивления воздуха, который пропорционален квадрату скорости поезда.
представляет собой совокупность дополнительных сопротивлений съездов, кривых и туннелей. Согласно Положению по расчету тяги поездов , это может быть получено как
представляет собой дополнительное сопротивление аппарели в: где и представляют высоту и длину откоса, соответственно.представляет дополнительное сопротивление кривой в: где представляет радиус кривой пути, и — длины поезда и кривой, соответственно, и — угол отклонения. представляет дополнительное сопротивление туннеля в: где представляет длину туннеля.
Параметры торможения поезда оцениваются точно и в реальном времени; очень важно точно определять тормозной путь, обеспечивать безопасность работы и повышать эффективность работы. Однако в реальном процессе эксплуатации поездов диапазон параметров торможения определяется опытом эксплуатации поездов, и тогда можно получить так называемый максимальный тормозной путь.Изменяющиеся во времени, дрейфующие и ненаблюдаемые характеристики параметров торможения не могут быть учтены указанным выше методом, что представляет большую угрозу для безопасной эксплуатации поездов. В настоящее время оценка постоянного параметра в линейной модели с гауссовым шумом является зрелым решением. Однако, как типично изменяющаяся во времени задача идентификации параметров нелинейной и негауссовской сложной системы, ей все еще не хватает эффективной теории и метода. Таким образом, эта статья улучшает традиционную максимизацию ожиданий, и максимизация математических ожиданий на основе скользящего окна была предложена для онлайн-идентификации изменяющихся во времени параметров торможения модели экстренного торможения высокоскоростного поезда.
3. Онлайн-идентификация модели экстренного торможения для высокоскоростных поездов
EM (максимизация ожидания) [23, 24] следует критерию максимального правдоподобия; ненаблюдаемые фиксированные параметры могут быть оценены с помощью EM на основе неполных наборов данных; получена офлайн-оценка параметров [25]. Для идентификации модели торможения поезда у EM есть некоторые недостатки, такие как низкая скорость идентификации, низкая вычислительная эффективность и автономная идентификация, не зависящая от времени.Поэтому предлагается максимизация математического ожидания на основе скользящего окна, и с помощью этого метода идентифицируются ненаблюдаемые параметры.
3.1. EM-идентификация модели торможения высокоскоростного поезда на основе скользящего окна
Скользящее окно — это общая модель обработки данных [26, 27]. С помощью скользящего окна можно обработать большое количество непрерывных, бесконечных и быстрых данных наблюдений за высокоскоростным поездом. Устанавливаются начальная и конечная позиции окон, и данные текущего окна выбираются для анализа.Начальная и конечная позиции окна изменятся с появлением новых данных измерения поезда. Старые данные будут удалены из окна, а новые данные будут добавлены в окно. Следовательно, входящие данные могут обрабатываться скользящим окном. И только последние данные поезда в окне могут быть обработаны, что согласуется с фактической сценой измерения процесса торможения поезда.
Уравнение (1) показывает, что модель поезда имеет марковские вероятностные свойства, а именно, где обозначает плотность вероятности того, когда задано состояние поезда, обозначает плотность вероятности того, когда задано состояние поезда, и является вектором неизвестного поезда. параметры торможения, которые могут быть нелинейными и изменяющимися во времени, например,
В этом документе размер скользящего окна делится на основе количества записей данных.Измерение в задается как передняя часть окна, а измерение в задано как задняя часть окна. Размер окна составляет, а длина скольжения составляет. Принимая окно в качестве объекта, результат идентификации параметра торможения, установленного в интервале, инициализируется как:
Последовательность выходных векторов окна и их функции правдоподобия определяются как где — плотность вероятности того, когда задана последовательность векторов смещения поезда. Учитывая характеристику идентификации максимального правдоподобия, последовательность векторов смещения логарифмируется с обеих сторон уравнения (12), и получается логарифмическая форма последовательности выходных векторов.
Уравнение (13) в сочетании с теоремой Байеса и марковскими характеристиками модели (1) получается следующим образом: где обозначает плотность вероятности того, когда задано состояние поезда. Поскольку модель поезда содержит неизмеримый набор параметров торможения, его трудно вычислить. В этой статье максимизация математического ожидания используется для косвенной оптимизации логарифмической функции правдоподобия уравнения (14). Последовательность состояний поезда рассматривается как неполные измеримые данные, а совместная функция плотности вероятности всех данных получается из выходных данных наблюдения поезда.
Принимая во внимание идею оценки минимальной дисперсии, предполагая, что текущее оценочное значение параметров поезда равно, ожидаемое значение вычисляется путем объединения с выходной последовательностью наблюдений. Где — плотность вероятности состояния, когда параметр поезда равен, а выходная последовательность равна данный.
3.1.1. Построение условного ожидания высокоскоростного поезда
На основании приведенного выше вывода в сочетании с теоремой Байеса и марковскими характеристиками модели торможения (1) выражается следующим образом:
Подставляя уравнение (17) в уравнение (16), условное математическое ожидание может быть получено: где, и относятся к плотности вероятности условного сглаживания, и, соответственно.Однако состояние поезда содержит неизмеримые переменные, которые затрудняют аналитический расчет путем интегрирования. Используя идею фильтра частиц и сглаживания частиц для справки, интегральный расчет решается методом частиц, оценивается фильтром частиц и оценивается сглаживателем частиц; обозначает вес частиц после фильтрации частиц и обозначает вес частиц после сглаживания. где и может быть решено уравнениями (22) и (23).Однако, поскольку уравнение (20) включает совместную условную плотность сглаживания двух переменных состояния с непрерывным временем и. Поэтому для дискретизации интегральных переменных и выбираются две группы частиц, которые также можно выразить как сумму частиц: где
На данный момент решены три компонента, и условного математического ожидания:
3.1. 2. Максимизация условных ожиданий высокоскоростного поезда
Анализируя модель торможения поезда, можно увидеть, что связь между условным математическим ожиданием и параметрами торможения поезда является нелинейной и невыпуклой, и трудно получить ее закрытое решение.Следовательно, оптимизация градиентного спуска [28] используется, чтобы найти, какой из них максимизируется, где представляет собой набор неизвестных параметров торможения, а частная производная по параметру выглядит следующим образом: где
После вычисления частной производной по параметр, градиентный метод используется для итерационной оптимизации параметров. Процесс итерации и обновления выглядит следующим образом: где — положительно определенная матрица для определения направления поиска градиента, и представляет собой скалярный шаг для обеспечения.В ходе итерационного процесса, описанного выше, когда приращение достигает установленного диапазона, процесс итерационной оптимизации прерывается. Оценка параметров делает и гарантирует, что это лучшая оценка, чем.
Когда эффект идентификации параметров торможения удовлетворяется, алгоритм завершается и рассматривает как окончательный результат идентификации набора параметров торможения окна; в противном случае алгоритм продолжает повторяться:
3.2. EM-идентификация скользящего окна модели торможения поезда
На основе анализа предыдущих разделов была получена интерактивная идентификация максимизации ожидания на основе скользящего окна для модели торможения высокоскоростного поезда.Блок-схема алгоритма показана на рисунке 1. Конкретные шаги алгоритма резюмируются следующим образом: (i) Шаг 1 . Данные наблюдений модели торможения высокоскоростного поезда собираются и записываются. Идентифицированный параметр торможения инициализируется. Размер скользящего окна, длина скользящего окна, серийный номер окна. Данные наблюдения за поездом идентифицируются EM. (Ii) Шаг 2 . Построить условное ожидание поезда (E): реализовать фильтр частиц и сглаживание частиц для вычисления, и ожидание поезда будет.(iii) Шаг 3 . Максимизировать ожидания поездов (M): параметр оценивается как. Когда точность идентификации удовлетворительна, итерация останавливается и получается результат идентификации параметра торможения окна. В противном случае он возвращается к шагу 2, чтобы продолжить итерационную оптимизацию. (Iv) Шаг 4 . Окно перемещается на длину назад: пусть и примем за начальное значение параметров торможения. Анализируются существующие данные окна. Шаги 2 и 3 выполняются итеративно.Результат идентификации параметров торможения получается и затем передается на этап 5. (v) Этап 5 . Если длина оставшихся данных больше, чем размер окна, перейдите к шагу 4. В противном случае оставшиеся данные будут использоваться в качестве идентификационных данных. Шаг 2 и Шаг 3 выполняются для получения результата идентификации параметров торможения последнего окна.
4. Результаты и анализ моделирования
Для проверки эффективности метода идентификации в качестве объекта исследования выбран четырехмоторный и четырехприцепной высокоскоростной поезд CRh4 и проведен имитационный эксперимент. .
4.1. Объяснение экспериментальных параметров
В эксперименте по моделированию торможения поезда основные параметры тормозного устройства показаны в таблице 1.
| ||||||||||||||||||||||||||||
Таблица 1 показывает, что коэффициент трения тормозного диска и коэффициент торможения поезда являются постоянными параметрами, но в реальном процессе торможения поезда коэффициент трения тормозного диска будет изменяться нелинейно. с изменением скорости, а коэффициент торможения поезда будет немного колебаться по мере движения поезда.Таким образом, в этой статье будут определены ненаблюдаемый коэффициент трения тормозного диска и коэффициент торможения поезда.
Согласно TSI (Техническая спецификация взаимодействия) коэффициент сцепления тормозов показан в таблице 2.
| |||||||||||||||||||||||||
Предполагая, что уравнение состояния поезда нарушается негауссовым шумом, на примере однородного шума уравнение наблюдения нарушается гауссовым шум.
При идентификации модели поезда количество итераций — 50, количество частиц — 20, а начальные значения коэффициента трения и передаточного отношения устанавливаются на случайные числа в пределах 100% от реального значения.На основе вышеупомянутой среды моделирования проводится 200 экспериментов Монте-Карло для определения параметров торможения высокоскоростных поездов в реальном времени.
4.2. Определение коэффициента трения тормозного диска
В реальном процессе торможения поезда коэффициент трения тормозного диска будет нелинейно изменяться с изменением скорости. На рисунке 2 показана идентификационная кривая коэффициента трения тормозного диска в реальном времени. Сплошная красная линия представляет собой кривую реального изменения коэффициента трения поезда, изменяющегося в зависимости от скорости движения.Черные, синие и фиолетовые сплошные линии — это кривые идентификации коэффициента трения с начальными значениями 0,40, 0,35 и 0,03 соответственно. Черные, синие и фиолетовые пунктирные линии — это идентификационные кривые коэффициента трения с начальными значениями 0,15, 0,20 и 0,25 соответственно.
Можно видеть, что на трех этапах замедления, и предлагаемый метод может точно определить коэффициент трения тормозного диска в реальном времени. На этапе замедления, поскольку коэффициент трения слишком мал и есть точка перегиба с более высокой скоростью изменения, точность идентификации немного снижается, но она может точно предсказать тенденцию изменения коэффициента трения тормозного диска, что обеспечивает ориентир для определение параметров торможения и мониторинг эффективности торможения поездов.
На рисунках 3 и 4 показаны кривые ошибки идентификации и относительной погрешности передаточного отношения соответственно. Из рисунков видно, что погрешность идентификации и относительная погрешность при различных начальных значениях постепенно уменьшаются с увеличением времени, а флуктуации двух кривых постепенно уменьшаются и после этого остаются практически неизменными в фиксированном диапазоне.
Чтобы дополнительно доказать эффективность этого метода, предложенного в этой статье, этот метод сравнивается с расширенным фильтром Калмана (EKF).EKF — это типичное расширение линейного фильтра Калмана в теории и применении. Его теоретическая суть состоит в том, чтобы линеаризовать нелинейную функцию, то есть взять выражение первого порядка разложения Тейлора для реализации оценки оптимальной линейной задачи. Новшеством его применения в оценке состояния является точный расчет матрицы усиления. В этом процессе системный шум и шум измерений интегрируются в обновление матрицы усиления, так что алгоритм имеет лучшую точность оценки и способность противодействовать помехам.На рисунках 5–7 показаны результаты идентификации в реальном времени, ошибки оценки и относительные ошибки коэффициента трения, соответственно, на основе EKF при различных начальных условиях.
Как видно из рисунков 5–7, по сравнению с EKF результаты идентификации, полученные с помощью предлагаемого в этой статье метода, могут быстро сходиться к истинному значению коэффициента трения. В процессе конвергенции колебание ошибки идентификации меньше.
В таблице 3 показано сравнение результатов оценки коэффициента трения между методом в этой статье и EKF при различных начальных значениях.
Из таблицы 3 видно, что средние значения ошибки оценки и относительной ошибки коэффициента трения, полученные с помощью метода, описанного в данной статье, равны ± 0. 0068 и 2.4807% соответственно, а средние значения ошибки оценки и относительной погрешности коэффициента трения, полученные EKF, составляют ± 0,0172 и 4,9278% соответственно. Метод, предложенный в этой статье, имеет более высокую точность оценки и лучшие характеристики в реальном времени, а результаты оценки соответствуют реальным потребностям тормозной системы. На рисунке 8 показана идентификационная кривая скорости торможения поезда с помощью онлайн-ЭМ и кривая расчета тормозного смещения. Для полной остановки требуется 94,2 секунды, а тормозной путь составляет 4647.16 метров, что соответствует национальному стандарту. 4.3. Определение коэффициента торможения поездаВ реальном процессе торможения поезда коэффициент торможения поезда непостоянен, и его значение будет незначительно колебаться в зависимости от движения поезда. На рисунке 9 показана идентификационная кривая в реальном времени передаточного отношения высокоскоростного поезда. Сплошная красная линия — это реальная кривая изменения передаточного отношения поезда. Сплошные черные, синие и фиолетовые линии — это кривые определения передаточного числа тормозов с начальными значениями 5, 4 и 3 соответственно.Черные, синие и фиолетовые пунктирные линии представляют собой кривые определения передаточного числа тормозов с начальными значениями 0, 1 и 2 соответственно. Из графика видно, что метод, предложенный в этой статье, позволяет точно определять передаточное отношение поездов в реальном времени, а точные результаты определения передаточного отношения могут быть получены после. На рисунках 10 и 11 показаны кривые ошибки идентификации и относительной погрешности передаточного числа торможения соответственно. Из рисунков видно, что погрешность идентификации и относительная погрешность при различных начальных значениях постепенно уменьшаются с увеличением времени, а флуктуации двух кривых постепенно уменьшаются и после этого остаются практически неизменными в фиксированном диапазоне. На рисунках 12–14 показаны результаты идентификации в реальном времени, ошибки оценки и относительные ошибки передаточного числа торможения, соответственно, на основе EKF при различных начальных условиях. Как видно из рисунков 12–14, по сравнению с EKF результаты идентификации, полученные с помощью предлагаемого в этой статье метода, могут быстро сходиться к истинному значению передаточного отношения. В процессе конвергенции колебание ошибки идентификации меньше. В таблице 4 показано сравнение результатов оценки передаточного отношения между методом в этой статье и EKF при различных начальных значениях.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

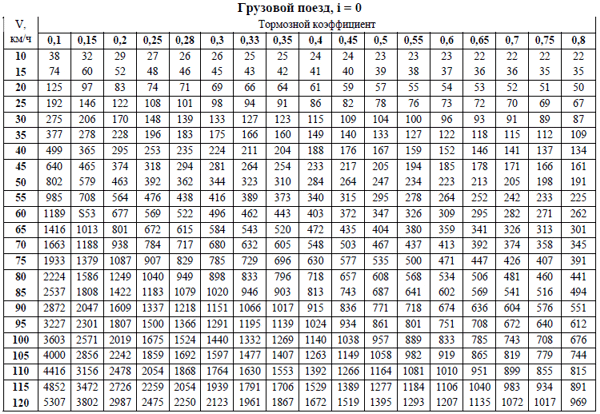 105
105 3
3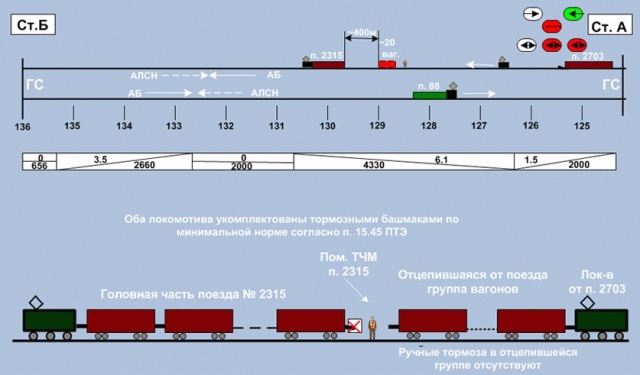 3
3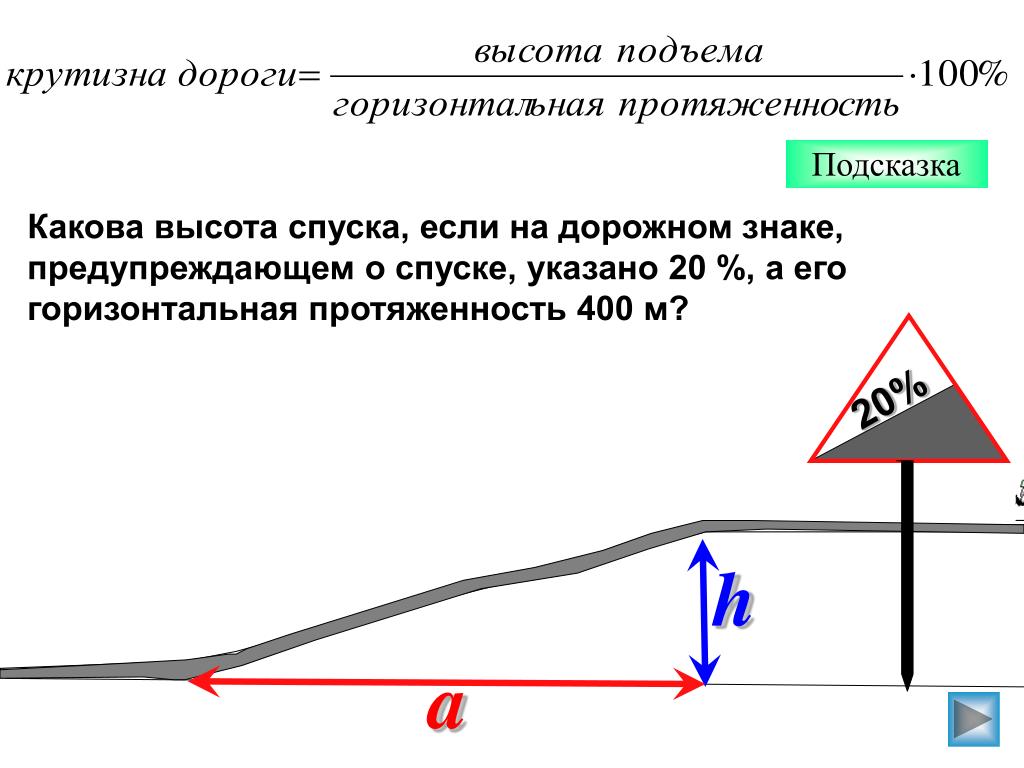 8bm + ох—ic, кгс/тс
8bm + ох—ic, кгс/тс