Пересечение прямой и окружности: Пересечение окружности и прямой.Координаты.

автор: alexxlab

Содержание

Пересечение окружности и прямой.Координаты.

Уравнение окружности
Уравнение прямой к угловым коэффициентом
Координаты пересечения окружности и прямой

Рассмотрим более подробно задачу пересечения окружности и прямой. В принципе само решение есть уже в общем виде Пересечение прямой и кривой второго порядка, но мы рассмотрим и выведем формулы  точек пересечения  этих двух геометрических объектов.

Уравнение прямой, как мы знаем из материала Расчет параметров прямой линии по заданным параметрам  могут быть заданы в нескольких видах: 

— в общем виде, 

— с угловым коэффициентом

— в нормальном  виде 

Что бы решить нашу первоначальную задачу, использовать будем уравнение прямой с угловым коэффициентом  которое имеет вид

Уравнение окружности  тоже может быть выражена в различных видах

Например в общем виде оно имеет вид

Подставим  в уравнение окружности, уравнение прямой

Раскроем скобки 

Или 

Мы получили стандартное квадратное уравнение, решив котрое  мы получим два значения, которые и будут являтся абсциссами точек пересечения прямой и окружности.

Подставим эти координаты в уравнение прямой, мы получим две ординаты  точек пересечения.

Таким образом решение найдено.

Для упрощения, для сверки результатов — калькулятор помогает Вам рассчитать  эти точки. Интересная особенность состоит в том, что прямая может быть задана в любом виде, хоть  виде двух точек.

А уравнение окружности  может быть не только введено с помощью коэффицентов, но и в виде пары трех координат через которые, эта окружность будет проходить.

 

  • Период нечетной дроби онлайн >>

ПЕРЕСЕЧЕНИЕ ПРЯМОЙ С ОКРУЖНОСТЬЮ | Математика

ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ Ж. АДАМАР

ПЕРЕСЕЧЕНИЕ ПРЯМОЙ С ОКРУЖНОСТЬЮ

ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ Ж. АДАМАР

Скачать всю книгу Ж. АДАМАР «ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ» в хорошем качестве
Ниже посмотрите текст для быстрого ознакомления(формулы отображаются не корректно):

57. Теорема. Через три точки, не лежащие на одной прямой
можно провести окружность и притом только одну.
Иначе говоря, окружность определяется тремя точками, не
лежащими на одной прямой.
Пусть, в самом деле, А, В, С (черт. 58) — три точки, не лежащие
на одной прямой линии. Мы уже доказали (п. 52), что перпендикуляры

восставленные в серединах отрезков
ВС, СА и АВ, проходят через одну
и ту же точку О, равноудалённую от точек
А, В и С. Окружность, описанная из
точки О, как из центра, радиусом О А, проходит

через три данные точки. Эта окружность—
единственная окружность, удовлетворяющая
поставленному условию, так как
центр окружности, которая пройдёт через
точки А, В и С, должен обязательно принадлежать трём перпендикулярам,
о которых мы говорили.
Следствие. Мы видим, что окружность не может иметь двух
различных центров, а следовательно, не может иметь и двух неравных
радиусов.
58. Теорема. Прямая не может пересекать окружность
более чем в двух точках.
Если расстояние от центра до прямой больше радиуса, прямая
не пересекает окружности. Если это расстояние меньше радиуса,
Р /1 И В Р’ прямая пересекает окружность
п двух точках.Наконец, если расстояние
равно радиусу, прямая имеет
с окружностью одну общую точку.
В последнем случае прямая назы-
q вается касательной к окружности.
Пусть дана окружность с центром
О и прямая D. Из центра О
(черт. 59) опустим на прямую D перпендикуляр ОН.
1°. Окружность не может иметь более двух общих точек с прямой
D. Это сводится к тому, что из точки О нельзя провести
к прямой D более двух наклонных, равных радиусу R (п. 30, следствие).

67 ПЕРЕСЕЧЕНИЕ ПРЯМОЙ С ОКРУЖНОСТЬЮ ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ Ж. АДАМАР

2°. Если расстояние ОН больше радиуса, то расстояние от центра

любой точки прямой и подавно (п. 29) будет больше радиуса;
следовательно, все точки прямой являются внешними по отношению
к кругу.
3°. Если, напротив, ОН меньше радиуса, точка Я находится внутри
окружности, но по обе стороны от Н есть точки, расположенные
вне окружности. Чтобы в этом убедиться, отложим на прямой D от
точки Н два отрезка HP и HP, равные радиусу; расстояния ОР
и ОР будут непременно больше радиуса. Следовательно,
будем иметь две точки пересечения
с окружностью: одну между Н и Р и другую —
между Н и Р\ это будут единственные точки
пересечения (1°).
4°. Если, наконец, ОН равно радиусу
(черт. 60), то точка Н будет общей точкой
прямой и окружности, но, так же как в 2°,
убедимся, что всякая другая точка прямой
находится вне окружности.

Следствие. Через точку, взятую на
окружности, можно провести к ней касательную
и только одну, причём эта касательная перпендикулярна
к радиусу, проведённому в эту точку.
59. Предыдущее определение касательной не годится в качестве
определения касательной к произвольной кривой.
Касательной к какой-либо кривой в точке М этой кривой (черт. 61)
называется предельное положение, к которому стремится прямая ММ\
когда точка М\ описывая кривую, безгранично
приближается к М.

Иначе
говоря:

Прямая МТназывается касательной
в точке Му если для всякого данного
угла е можно выбрать по обе стороны
от точки М две дуги ММХ и ММ2 такие,
чтобы для всякого положения точки
М\ взятой на одной из этих дуг, прямая ММ’ образовала бы
с прямой МТ или с её продолжением угол, меньший е *).
Покажем, что для случая окружности это определение сводится
к тому, которое мы дали выше.
Проведём в точке М окружности О перпендикуляр МТ к радиусу
ОМ и на хорду ММГ (черт. 62) опустим из центра перпендикуляр ОН.
Эта прямая является высотой равнобедренного треугольника ОММг

и в то же время биссектрисой угла при О. Угол ТММГ равен углу
МОН (как углы с перпендикулярными сторонами) и, следовательно, —
половине угла МОМ!. Но этот последний можно сделать меньше вся-
*) Можно доказать, как это вообще доказывается в теории пределов,
что если такая прямая существует, то она единственная,

68 ПЕРЕСЕЧЕНИЕ ПРЯМОЙ С ОКРУЖНОСТЬЮ ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ Ж. АДАМАР

кого данного угла, если выбрать точку М! достаточно близко
к точке М.
60. Нормалью к кривой в данной точке называется перпендикуляр
к касательной в этой точке. Следовательно, нормаль к окружности

в данной точке есть не что иное,
как радиус, проведённый в эту
точку.

На любой данной окружности имеются две (и только две) такие
точки, что нормали в этих точках проходят через данную точку Р
плоскости (отличную от центра): этими точками будут концы диаметра,
проходящего через точку Р.
60а. Углом между двумя кривыми в точке их пересечения
называется угол, образованный их касательными в этой точке (черт. 63).
Следовательно, угол между двумя пересекающимися окружностями
равен углу между радиусами, проведёнными в их общую точку, или
углу, ему пополнительному.
УПРАЖНЕНИЯ.
47. Из всех точек окружности проведены отрезки, равные и параллельные

одному и тому же данному отрезку.
Найти геометрическое место концов этих отрезков.
48. Найти геометрическое место середин отрезков, соединяющих данную
точку с различными точками окружности.
49. АВ — диаметр окружности О, С — точка, взятая на продолжении
этого диаметра за точку В, CDE— секущая из точки С, которая пересёкает
окружность в точках D и Е. Если внешняя часть CD равна радиусу, то
угол ЕОА в три раза больше угла DOB (доказать).

69 ПЕРЕСЕЧЕНИЕ ПРЯМОЙ С ОКРУЖНОСТЬЮ ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ Ж. АДАМАР

ПЕРЕСЕЧЕНИЕ ПРЯМОЙ С ОКРУЖНОСТЬЮ

Конспект урока «Пересечение прямой с окружностью»

Выполните тест №1. Ответы запишите в таблицу самооценки.

1.Сколько общих точек могут иметь две прямые?

2. С помощью каких инструментов строят перпендикулярные прямые?

А линейка, Б прямоугольный треугольник, В транспортир.

3.Чему равен радиус окружности, если ее диаметр равен 36см?

А 72см, Б 18см, В 9см, Г 36 см.

4.Расстояние от центра окружности, радиус которой равен 10см, до любой ее точки равно:

А 5см, Б 10см, В 20см, Г 1дм.

5.Прямая а не пересекает окружность. Расстояние от центра окружности до прямой а

А равно радиусу, Б меньше радиуса, В больше радиуса.

3.Игра «Верю, не верю». А сейчас давайте поиграем в игру «Верю, не верю». Вам необходимо внимательно прочитать высказывание и если вы с ним согласны, то в клеточке рядом с высказываем, ставите «+», если не согласны, то «-». Помогут вам в игре выдержки из книг Г. Глейзера «История математики в школе» и С. Акимова «Занимательная математика».

. Верите ли вы, что самая простая из кривых линий – окружность?

. Верите ли вы, что древние индийцы считали самым важным элементом окружности радиус, хотя не знали такого слова?

. Верите ли вы, что впервые термин “радиус” встречается лишь в 16 веке?

-Верите ли вы, что в переводе с латинского радиус означает “луч”?

. Верите ли вы, что при заданном периметре именно окружность ограничивает наибольшую площадь?

. Верите ли вы, что в русском языке слово “круглый” означает высшую степень чего-либо?

-Верите ли вы, что выражение “ходить по кругу” когда-то означало “прогресс”?

Верите ли вы, что хорда в переводе с греческого означает “струна”?

. Верите ли вы, что определение “касательной” уже есть в первом учебнике геометрии — “Начала” Евклида?

Текст для игры «Верю, не верю»

Самая простая из кривых линий – окружность. Это одна из древнейших геометрических фигур. Ещё вавилоняне и древние индийцы считали самым важным элементом окружности – радиус. Слово это латинское и означает “луч”. В древности не было этого термина: Евклид и другие учёные говорили просто “прямая из центра”, Ф. Виет писал что “радиус” — это “элегантное слово”. Общепринятым термин “радиус” становится лишь в конце XVII в. Впервые термин “радиус” встречается в “Геометрии” французского ученого Рамса, изданной в 1569 году.

В Древней Греции круг и окружность считались венцом совершенства. Действительно в каждой своей точке окружность “устроена” одинаково, что позволяет ей как бы двигаться “по себе”. На плоскости этим свойством обладает еще лишь прямая. Одно из интереснейших свойств круга состоит в том, что он при заданном периметре ограничивает максимальную площадь.

В русском языке слово “круглый” тоже стало означать высокую степень чего-либо: “круглый отличник”, “круглый сирота” и даже “круглый дурак”.

Если вы когда-либо пробовали получить информацию от бюрократической организации, вас, скорее всего “погоняли по кругу”. Фраза “ходить по кругу” обычно не ассоциируется с прогрессом. Но в период индустриальной революции, выражение “ходить по кругу” очень точно отражало прогресс. Шкивы и механизмы давали машинам возможность увеличить производительность и значит сократить рабочую неделю.

Без понятия круга и окружности было бы трудно говорить о круговращении жизни. Круги повсюду вокруг нас. Окружности и циклы идут, взявшись за руки. Циклы получаются при движении по кругу. Мы изучаем циклы земли, они помогают нам разобраться, когда надо сажать растения и когда мы должны вставать.

Представление об окружности даёт линия движения модели самолёта, прикреплённого шнуром к руке человека, также обод колеса, спицы которого соответствуют радиусам окружности.

Термин “хорда” (от греческого “струна”) был введён в современном смысле европейскими учёными в XII-XIII веках.

Определение касательной как прямой, имеющей с окружностью только одну общую точку, встречается впервые в учебнике “Элементы геометрии” французского математика Лежандра (1752-1833 гг.). В “Началах” Евклида даётся следующее определение: прямая касается круга, если она встречает круг, но при продолжении не пересекает его

По материалам книг: Г. Глейзер “История математики в школе”, С Акимова “Занимательная математика”.

Оцените результаты игры,если все верно, то в таблицу самооценки ставите 2 балла, если верно выполнено 7 заданий – 1 балл, иначе 0 баллов.

4. Изучение нового материала. Сейчас вам предстоит решить основную задачу сегодняшнего урока: Даны окружность радиуса r и прямая а, не проходящая через центр О окружности. Расстояние от точки О до прямой а равно d. Сколько общих точек пересечения могут иметь данные окружность и прямая? Ваши предложения по решению задачи. Работаем в парах. (Возьмите заготовленные вами модели окружности, карандаш, который будет служить моделью прямой, и, прикладывая карандаш к окружности, рассмотрите все возможные случаи их расположения. Сколько возможных вариантов вы заметили? Теперь результаты своих исследований зарисуйте в листах наблюдений, которые лежат у вас на партах.

ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ОКРУЖНОСТИ(Пересечение прямой с окружностью

Проведите прямую.

Рассмотрите все возможные варианты.


2

Сколько общих точек у окружности и прямой?

3

Найдите расстояние от центра окружно-

сти до прямой и сравните его с радиусом.

4

Сделайте вывод о взаимном расположении прямой и окружности, в зависимости от радиуса и расстояния от центра до прямой.

Докажем теперь наши предположения.

Учитель: значит, вы утверждаете, что если d<r, то прямая и окружность пересекаются 2 раза, не меньше и не больше. Докажем это.

Пусть r – радиус окружности

d – расстояние от точки О до прямой а

а) как найти расстояние от точки О до прямой а? ОНа ОН= d

б) на прямой а отложить отрезки НА=НВ=

ОА2=ОН2+НА2=d2+r2 — d2=r2, ОА=r  точка А лежит на окружности.

ОВ=ОА= r  точка В лежит на окружности.

Таким образом, прямая а и окружность имеют 2 общие точки.

Доказательство того, что прямая а и окружность не имеют других общих точек вы разберете дома самостоятельно

Утверждение, что если d=r, то окружность и прямая имеют одну общую точку докажет ученик.

О

ОН= r  точка Н лежит на окружности.

Единственность общей точки доказывается с помощью вывода.

Для любой точки М прямой а: ОН – перпендикуляр, ОМ — наклонная к прямой а ОМ> ОН ОМ> r  точка М не лежит на окружности

Третий случай вы докажете самостоятельно дома, что если d>r, то прямая и окружность не пересекаются

5.Решение задач.

В таблице даны радиус окружности и расстояние от центра этой окружности до некоторой прямой.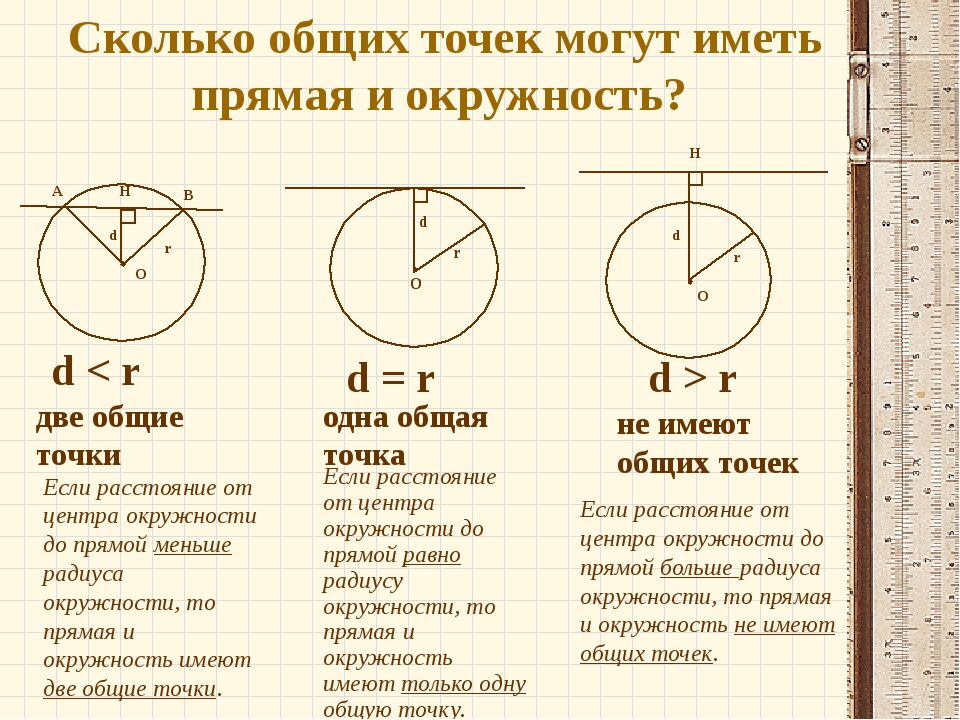 Что можно сказать о взаимном расположении прямой и окружности в каждом случае? Проверьте себя, выполнив построения.

Условие задачи в виде таблицы записано на доске.

6. Работа с тестом. Тесты выданы заранее. В течении 3-х минут учащиеся отвечают на вопросы теста и заносят ответы в тетрадь. Проверим правильность выполнения теста, – если все верно, то в таблицу самооценки ставите 2 балла, если допущена одна, две ошибки – 1 балл, иначе 0 баллов.

А.

Б.Самостоятельная работа по карточкам

Проведите прямые через каждые две точки. Сколько общих точек имеет каждая из прямых с окружностью.

Ответ.

Прямая ______ и окружность не имеют общих точек.

Прямая ______ и окружность имеют только одну ___________ точку.

Прямые ______, _______, ________, _______ и окружность имеют две общие точки.

7.Подведение итогов урока. Какие открытия вы сделали сегодня на уроке? Чему вы научились на уроке?

Выставление оценок за урок.

Ключ для выставления оценки:

Домашнее задание .

python — Какой самый эффективный способ найти пересечение прямой и окружности в Python?

У меня многоугольник состоит из множества точек. Я хочу найти пересечение многоугольника и круга. Предоставив центр окружности [x0, y0] и радиус r0, я написал грубую функцию для простого решения квадратного уравнения окружности и линии. Но как насчет эффективности найти пересечение каждого отрезка прямой многоугольника один за другим? Есть ли более эффективный способ?

Я знаю, что Simpy уже предоставляют возможность получить пересечения различной геометрии. Но также как насчет эффективности внешней библиотеки, такой как sympy, по сравнению с ее вычислением по моей собственной функции , если я хочу иметь дело с большим количеством полигонов?

 
def LineIntersectCircle(p,lsp,lep):
# p is the circle parameter, lsp and lep is the two end of the line
  x0,y0,r0 = p
  x1,y1 = lsp
  x2,y2 = esp
  if x1 == x2:
    if abs(r0) >= abs(x1 - x0):
        p1 = x1, y0 - sqrt(r0**2 - (x1-x0)**2)
        p2 = x1, y0 + sqrt(r0**2 - (x1-x0)**2)
        inp = [p1,p2]
        # select the points lie on the line segment
        inp = [p for p in inp if p[1]>=min(y1,y2) and p[1]<=max(y1,y2)]
    else:
        inp = []
  else:
    k = (y1 - y2)/(x1 - x2)
    b0 = y1 - k*x1
    a = k**2 + 1
    b = 2*k*(b0 - y0) - 2*x0
    c = (b0 - y0)**2 + x0**2 - r0**2
    delta = b**2 - 4*a*c
    if delta >= 0:
        p1x = (-b - sqrt(delta))/(2*a)
        p2x = (-b + sqrt(delta))/(2*a)
        p1y = k*x1 + b0
        p2y = k*x2 + b0
        inp = [[p1x,p1y],[p2x,p2y]]
        # select the points lie on the line segment
        inp = [p for p in inp if p[0]>=min(x1,x2) and p[0]<=max(x1,x2)]
    else:
        inp = []
  return inp

17

xibinke 15 Июн 2015 в 14:51

4 ответа

Лучший ответ

Я думаю, возможно, ваш вопрос о том, как в теории сделать это как можно быстрее.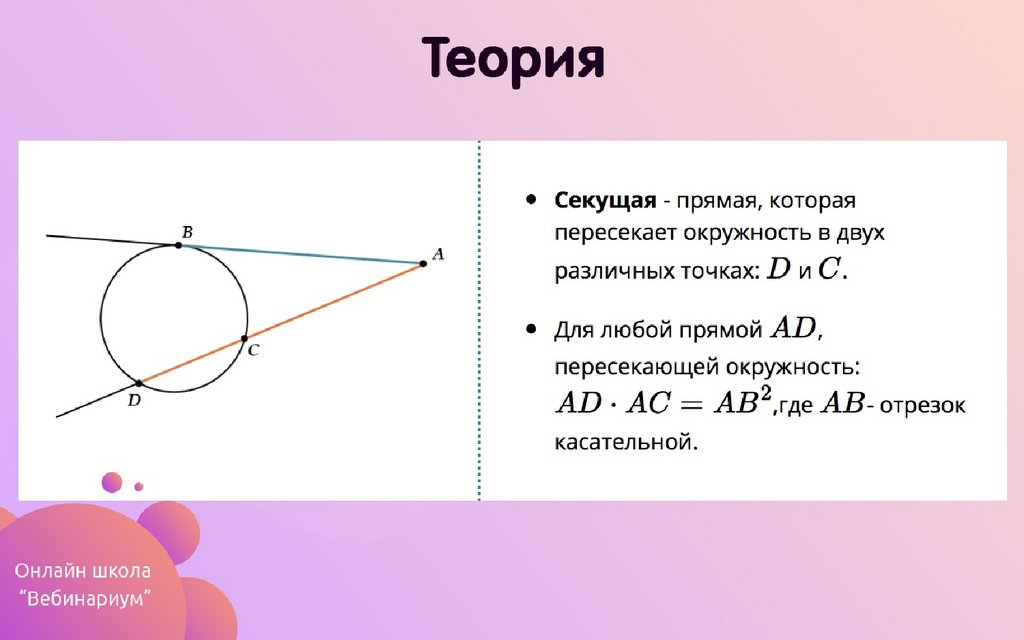 Но если вы хотите сделать это быстро, вы должны действительно использовать что-то написанное на C / C ++.

Я довольно привык Shapely, поэтому приведу пример, как это сделать с этой библиотекой , Есть много геометрических библиотек для Python. Я перечислю их в конце этого ответа.

from shapely.geometry import LineString
from shapely.geometry import Point

p = Point(5,5)
c = p.buffer(3).boundary
l = LineString([(0,0), (10, 10)])
i = c.intersection(l)

print i.geoms[0].coords[0]
(2.8786796564403576, 2.8786796564403576)

print i.geoms[1].coords[0]
(7.121320343559642, 7.121320343559642)

Что немного противоречит в Shapely, так это то, что круги — это границы точек с буферными областями. Вот почему я делаю p.buffer(3).boundry

Кроме того, пересечение i является списком геометрических фигур, в данном случае они обе являются точками, поэтому я должен получить их оба из i.geoms[]

Существует еще один вопрос Stackoverflow, в котором подробно рассказывается об этих библиотеках для заинтересованных лиц.

РЕДАКТИРОВАТЬ, потому что комментарии:

Shapely основан на GEOS (trac.osgeo.org/geos), который построен на C ++ и значительно быстрее, чем все, что вы пишете в Python. Кажется, что SymPy основан на mpmath (mpmath.org), который также выглядит как python, но, похоже, в него интегрировано много довольно сложной математики. Реализация этого самостоятельно может потребовать большой работы и, вероятно, не будет такой быстрой, как реализация GEOS C ++.

12

Community 23 Май 2017 в 12:29

Дешевая пространственная перегородка может быть разделить самолет на 9 частей

Вот дерьмовая диаграмма. Представьте, если хотите, что линии просто касаются круга.

  | |
__|_|__
__|O|__
  | |
  | |

8 из интересующих нас областей окружают круг. Квадрат в центре не очень полезен для дешевого теста, но вы можете поместить квадрат r/sqrt(2) внутри круга, так что его углы просто касаются круга.

Давайте обозначим области

A |B| C
__|_|__
D_|O|_E
  | |
F |G| H

И квадрат r/sqrt(2) в центре мы будем называть J

Мы назовем набор точек в центральной части, показанной на диаграмме, которых нет в J, Z

Пометьте каждую вершину многоугольника буквенным кодом.

Теперь мы можем быстро увидеть

AA => Outside
AB => Outside
AC => Outside
...
AJ => Intersects
BJ => Intersects
...
JJ => Inside

Это может превратиться в таблицу поиска

Таким образом, в зависимости от вашего набора данных, вы, возможно, сэкономили себе массу работы. Однако все, что имеет конечную точку в Z, необходимо проверить.

1

John La Rooy 16 Июн 2015 в 09:10

Вот решение, которое вычисляет пересечение окружности с линией или отрезком, определяемым двумя (x, y) точками:

def circle_line_segment_intersection(circle_center, circle_radius, pt1, pt2, full_line=True, tangent_tol=1e-9):
    """ Find the points at which a circle intersects a line-segment.   This can happen at 0, 1, or 2 points.

    :param circle_center: The (x, y) location of the circle center
    :param circle_radius: The radius of the circle
    :param pt1: The (x, y) location of the first point of the segment
    :param pt2: The (x, y) location of the second point of the segment
    :param full_line: True to find intersections along full line - not just in the segment.  False will just return intersections within the segment.
    :param tangent_tol: Numerical tolerance at which we decide the intersections are close enough to consider it a tangent
    :return Sequence[Tuple[float, float]]: A list of length 0, 1, or 2, where each element is a point at which the circle intercepts a line segment.

    Note: We follow: http://mathworld.wolfram.com/Circle-LineIntersection.html
    """

    (p1x, p1y), (p2x, p2y), (cx, cy) = pt1, pt2, circle_center
    (x1, y1), (x2, y2) = (p1x - cx, p1y - cy), (p2x - cx, p2y - cy)
    dx, dy = (x2 - x1), (y2 - y1)
    dr = (dx ** 2 + dy ** 2)**. 5
    big_d = x1 * y2 - x2 * y1
    discriminant = circle_radius ** 2 * dr ** 2 - big_d ** 2

    if discriminant < 0:  # No intersection between circle and line
        return []
    else:  # There may be 0, 1, or 2 intersections with the segment
        intersections = [
            (cx + (big_d * dy + sign * (-1 if dy < 0 else 1) * dx * discriminant**.5) / dr ** 2,
             cy + (-big_d * dx + sign * abs(dy) * discriminant**.5) / dr ** 2)
            for sign in ((1, -1) if dy < 0 else (-1, 1))]  # This makes sure the order along the segment is correct
        if not full_line:  # If only considering the segment, filter out intersections that do not fall within the segment
            fraction_along_segment = [(xi - p1x) / dx if abs(dx) > abs(dy) else (yi - p1y) / dy for xi, yi in intersections]
            intersections = [pt for pt, frac in zip(intersections, fraction_along_segment) if 0 <= frac <= 1]
        if len(intersections) == 2 and abs(discriminant) <= tangent_tol:  # If line is tangent to circle, return just one point (as both intersections have same location)
            return [intersections[0]]
        else:
            return intersections

0

Peter 3 Янв 2020 в 17:16

Я думаю, что формула, которую вы используете, чтобы найти координаты двух пересечений, не может быть оптимизирована дальше.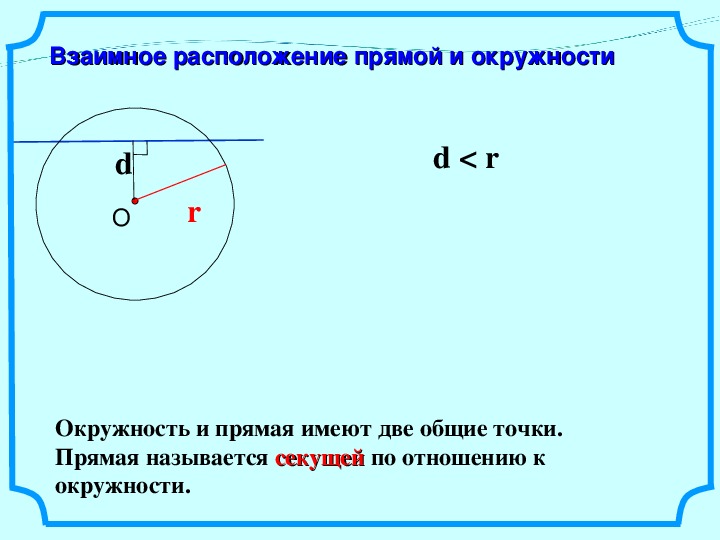 Единственное улучшение (которое имеет числовое значение) состоит в том, чтобы различать два случая: |x_2-x_1| >= |y_2-y_1| и |x_2-x1| < |y_2-y1|, так что величина k всегда находится между -1 и 1 (в ваших вычислениях вы можете получить очень высокие числовые ошибки, если | x_2-x_1 | очень мало). Вы можете поменять местами x-s и y-s, чтобы свести один случай к другому.

Вы также можете выполнить предварительную проверку: если обе конечные точки находятся внутри круга, пересечения нет. При вычислении квадрата расстояния от точек до центра круга это становится простой формулой, в которой не используется функция квадратного корня. Другая проверка: «находится ли линия вне круга» уже реализована в вашем коде и соответствует дельте

0

Emanuele Paolini 15 Июн 2015 в 14:52

Пересечение прямой и окружности.

— Черчение
Пересечение прямой с окружностью Рассмотрим вопрос о пересечении прямой с окружностью. Пусть R — радиус окружности и d — расстояние от центра окружности до прямой. Примем центр окружности за начало координат, а прямую, перпендикулярную к данной, за ось х (рис. 179). Тогда уравнением окружности будет x’2 + y2=R2, а уравнением прямой x = d. Для того чтобы прямая и окружность пересекались, надо, чтобы система двух уравнений x’2 + y2=R2, x = d имела решение. И обратно: всякое решение этой системы дает координаты X, у точки пересечения прямой с окружностью. Решая нашу систему, получим: Из выражения для у видно, что система имеет два решения, т. е. окружность и прямая имеют две точки пересечения, если R>d (рис. 179,а). Система имеет одно решение, если R=d (рис. 179,в). В этом случае прямая и окружность касаются. Система не имеет решения, т. е. прямая и окружность не пересекаются, если R<.d (рис. 179, в).

2.ДОКАЖИТЕ, ЧТО ЕСЛИ У ПАРАЛЛЕЛОГРАММА ДИАГОНАЛИ ПЕРПЕНДИКУЛЯРНЫ, ТО ОН ЯВЛЯЕТСЯ РОМБОМ.

  Дано: АВСD-параллелограмм АС┴BD
Док-ть: АВСD-ромб
Доказательство:  

БИЛЕТ№9.

1.ЗНАЧЕНИЕ СИНУСА, КОСИНУСА, ТАНГЕНСА И КОТАНГЕНСА НЕКОТОРЫХ УГЛОВ (45°, 30°,60°).

2.ДОКАЖИТЕ, ЧТО ЕСЛИ ДИАГОНАЛИ ПРЯМОУГОЛЬНИКА ПЕРЕСЕКАЮТСЯ ПОД ПРЯМЫМ УГЛОМ, ТО ОН ЯВЛЯЕТСЯ КВАДРАТОМ.

  Дано: АВСD-прямоугольник АС┴BD
Док-ть АВСD-квадрат
Доказательство    

БИЛЕТ№10.

1.ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА.

ТЕОРЕМА ФАЛЕСА.

Теорема: Если параллельные прямые отсекают на одной стороне угла равные отрезки, то они отсекают равные отрезки и на другой его стороне.
  Дано: ∟COD A1B1 ∥ A2B2 ∥ A3B3, A1, A2, A3 ∈ OC, B1, B2, B3 ∈ OD, A1A2=A2A3.
Док-ть B1B2=B2B3.
Доказательство 1) Через точку B2 проведем прямую EF, EF ∥ A1A3. 2) Рассмотрим четырехугольник A1FB2A2. — A1F ∥ A2B2 (по условию), — A1A2 ∥ FB2 (по построению).Следовательно, A1FB2A2 — параллелограмм (по определению). По свойству противолежащих сторон параллелограмма, A1A2=FB2. 3) Аналогично доказываем, что A2B2EA3 — параллелограмм и A2A3=B2E. 4) Так как A1A2=A2A3 (по условию), то FB2=B2E. 5) Рассмотрим треугольники B2B1F и B2B3E. — FB2=B2E (по доказанному), — ∠B1B2F=∠B2EB3 (как вертикальные), — ∠B2FB1=∠B2EB3 (как внутренние накрест лежащие при A1B1 ∥ A3B3 и секущей EF). Следовательно, треугольники B2B1F и B2B3E равны (по стороне и двум прилежащим к ней углам). Из равенства треугольников следует равенство соответствующих сторон: B1B2=B2B3. Что и требовалось доказать.

Билет№11.

1.СООТНОШЕНИЕ МЕЖДУ СТОРОНАМИ И УГЛАМИ В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ (ОПРЕДЕЛЕНИЕ).

   

2. ДОКАЗАТЬ ТЕОРЕМУ О СРЕДНЕЙ ЛИНИИ ТРАПЕЦИИ.

Теорема:
  Дано: ΔАВСД-данная трапеция QP-средняя линия
Док-ть QP║ BC, QP║AD QP =1/2 (BC+ AD)
Доказательство      

Билет№12.

1.ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ (ОПРЕДЕЛЕНИЕ).

 

2. ДОКАЖИТЕ,ЧТО СЕРЕДИНЫ СТОРОН ЧЕТЫРЕХУГОЛЬНИКА ЯВЛЯЮТСЯ ВЕРШИНАМИ ПАРАЛЛЕЛОГРАММА.

  Дано: ΔАВС-треугольник ЕД-средняя линия
Док-ть ЕД║АВ,ЕД=1/2АВ
Доказательство: Проведем диагональ АС в четырехугольнике АВСД.АС разбивает четырехугольник на 2 треугольника АВС и АДС. Проведем средние линии в треугольниках КМ и ОN. КМ — средняя линия ΔАВС(по определению), тогда КМ = АС/2 и КМ ║ АС. ON- средняя линия ΔADC, значит ON = AC/2 и ON ║АС Получаем, что KM=ON и KM параллельна ON(это признак!) Если две стороны четырехуг. равны и параллельны, то четырехуг. — параллелограмм.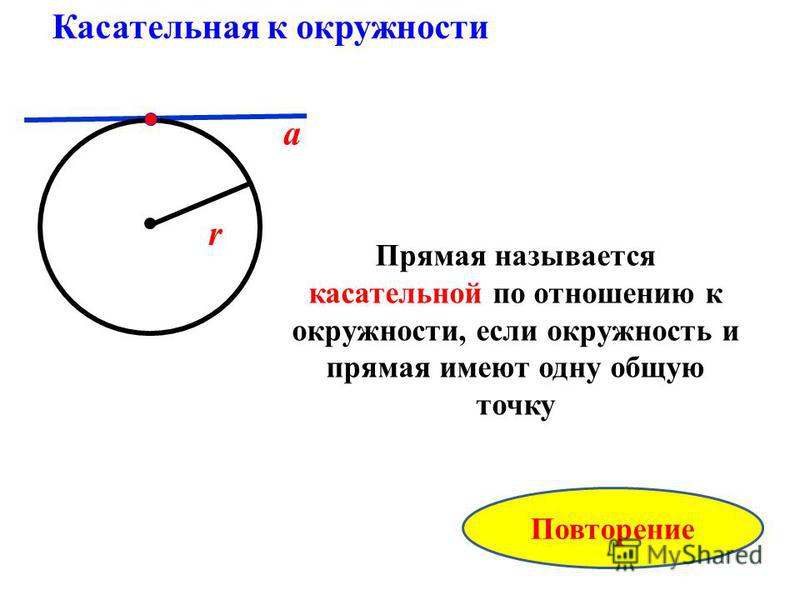 Значит KMNO параллелограм.  

Билет№13.

1.СИНУС, КОСИНУС И ТАНГЕНС ОСТРОГО УГЛА ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА (ОПРЕДЕЛЕНИЕ).

2.ДОКАЗАТЬ ТЕОРЕМУ О СРЕДНЕЙ ЛИНИИ ТРЕУГОЛЬНИКА.

Теорема:
  Дано: ΔАВС-треугольник ЕД-средняя линия
Док-ть ЕД║АВ,ЕД=1/2АВ
Доказательство

Билет№14.

Пересечение прямой с окружностью

здравствуйте тема эти главы взаимное расположение прямой окружности как то наверняка знаете из школьного курса геометрии прямая может либо не пересекаться с окружности либо иметь одну точку пересечения с ней в таком случае говорится что прямая касается окружности ибо же прямая кружится могут пересекаться в двух точках но давайте попытаемся найти количество точек пересечения и их координат возьмем такую систему координат чтобы центра кроме стен зовем кивагор совпал с начала координат точки пересечения прямой и окружности для завел p1 и p2 соответственно выберем 2 произвольной точки на прямой назовем их мыл и построим вектор-м как вы наверняка знаете вектор сдается координатами одной точке его концов то в том случае если его начал перенести в началу координат назовем этот вектор r штрих теперь найдем ближайшей точке о точку напрямую назовем ее рука посмотрим что должно выполняться этой точке поскольку к ближайшая точка напрямую для от то угол о кп-2 или о кп-1 должен быть прямым но аналогичные угол к о н 4-х должен быть также прим потому что он штрих параллельна m значит если мы посмотрим на виктора ока и опыт штрих они должны быть перпендикулярны друг другу значит их скалярное произведение должно быть нулю но также очевидно что для точки к должно выполняться уравнение прямой на которой лежит то есть y + ну теперь посмотрим у нас есть система из двух линейных уравнений с двумя неизвестными ну значит можно найти координаты точки к а значит и расстояние подхода к теперь посмотрим если расстояние от а до к больше чем радиус окружности значит прямая и окружность и не пересекались если расстояние от а до к равняется радиусу окружности значит прямая касается окружности и к является точки касания если же расстояние отвода к меньше радиуса то мы можем найти точки касания таким образом мы знаем раним сократить это лишь на расстоянии от а до к не знаю что google о кп-2 и о кр-1 прямые значит по теореме пифагора мы можем найти расстояние до b2 и b1 от к ну после того как мы знаем установить расстояние от k до b2 и также с учетом того что мы знаем что к ним по 2 лежат на прямой создающийся уравнением по x плюс y плюс z равно нулю мы можем найти координаты точки p 2 а также координаты точки p 1 вот мы нашли точку пересечения прямой что нам и требуется спасибо за внимание надеюсь этот урок был вам полезен и до свидания я не буду это

по геометрии «Взаимное расположение прямой и окружности» для 8 класса | План-конспект урока по геометрии (8 класс) по теме:

Конспект «открытого» урока

Дидактическая цель: формирование новых знаний.

Цели урока:

обучающие: сформировать математические понятия: расстояние от центра окружности до прямой, взаимное расположение прямой и окружности, добиться понимания и воспроизведения учащимися данных понятий через выполнение практической работы исследовательского характера.

развивающие: развивать у учащихся познавательный интерес, умение объяснять, обобщать, анализировать и систематизировать полученные результаты, сравнивать, сопоставлять, делать выводы.

воспитательные: воспитание средствами математики культуры личности.

здоровьесберегающие: создание благоприятного психологического климата на уроке.

Планируемый результат:

  • Предметные умения: закрепят знания об окружности, ее радиусе, диаметре, хорде, изучат взаимное расположение прямой и окружности, продолжат развивать умения в составлении кластеров и заполнении таблиц.
  • Личностные: формирование ответственного отношения к учению, готовности к саморазвитию и самообразованию, формирование коммуникативной компетенции в общении и сотрудничестве со сверстниками, формирование и развитие интереса к математике.
  • Регулятивные: осуществление регулятивных действий самонаблюдения, самоконтроля, самооценки в процессе практической деятельности.
  • Познавательные: построение логических рассуждений, включающее установление причинно-следственных связей, анализ и синтез объектов.
  • Коммуникативные: формулировка собственного мнения и позиции, способность аргументировать и координировать ее с позициями партнеров  в сотрудничестве при выработке общего решения в совместной деятельности; умение задавать вопросы  и отвечать на них; адекватно использовать речевые средства для решения различных коммуникативных задач.

Формы обучения:

  • по содержанию – беседа, практическая работа;
  • по организации деятельности – индивидуальная, фронтальная, работа в парах.

Оборудование и материалы: проектор, экран, ноутбук, презентация, раздаточный материал (индивидуальные карты знаний, листы с лабораторной работой, полоски самоклеящейся бумаги), циркуль, угольник, карандаш.

План урока:

  1. Организационный момент (1 минута)
  2. Актуализация знаний и умений (5 – 7 минуты)
  3. Целеполагание и мотивация (3 – 5 минут)
  4. Изучение нового материала (5 – 7 минут)
  5. Физ.минутка (2 – 3 минуты)
  6. Первичное осмысление и закрепление знаний (5 – 7 минут)
  7. Закрепление изученного материала, решение задач (15 – 17 минут)
  8. Рефлексивно-оценочный этап (2 – 3 минуты)
  9. Домашнее задание (2 – 3 минуты)

Этапы
урока

Задачи этапа

Визуальный ряд

Деятельность учителя

Осуществляемая деятельность
учащихся

Формы организации
совзаимодействия

Формируемые умения

(универсальные
учебные действия)

1

2

3

4

5

6

I. Организационный момент

Эмоциональная, психологическая подготовка

Слайд 1,2

Приветствие учащихся, проверка готовности

к уроку

Демонстрируют готовность к уроку

Фронтальная

Регулятивные: контролируют свои действия

Личностные: умение с достаточной полнотой и точностью выражать свои  мысли, слушать г

II.

Актуализация знаний и умений

Продемонстрировать необходимость  знания точного  определения.

Слайд 3

Слайд 4

Вступительное слово учителя.

Давайте поиграем в игру «Верю – не верю». У каждого из вас есть на столе индивидуальная карта знаний. Запишите на ней свои Ф.И. и заполните таблицу 1 для игры. (Цель игры: Вызвать интерес к изучению темы “окружность”, создать положительную мотивацию самостоятельного изучения текста по теме.)

А теперь прочитайте текст на листе 2. Сравните ответы с теми, что были в таблице «Верю – не верю».

Участвуют в беседе с учителем, отвечают на поставленные вопросы, заполняя таблицу.

Читают текст и корректируют свои ответы.

 

Индивидуальная работа, работа с текстом

Познавательные  Поиск и выделение необходимой информации

Регулятивные Выделение и осознание того, что уже пройдено.

Постановка цели учебной задачи, синтез

Коммуникативные Умение с достаточной полнотой и точностью выражать свои  мысли, слушать и вступать в диалог

III.

Целеполагание и мотивация

Определить тему и цели урока.

Слайд 5

Слайд 6

Слайд 7

Слайд 8

Слайд 9,10

1. Учитель продолжает  беседу с проблемными вопросами по будущей теме урока. Просит составить вопросы по тексту и заполнить таблицу в индивидуальной карте знаний. Предлагает обменяться листами с соседом по парте и ответить на его вопросы.

При необходимости задает учащимся наводящие вопросы, комментирует.

2. Так о какой фигуре пойдет речь на уроке? Какие ассоциации возникают со словом окружность. Заполните кластер.

3. Вместе с учениками определяет тему урока и учебные задачи   

4. Изучите таблицу 3. Сформулируйте геометрические определения понятий, используя ключевые слова. Дополните первый столбец таблицы.

1.Участвуют в работе, в беседе с учителем, составляют вопросы, работают с текстом,  заполняют индивидуальную карту заданий.

2.Речь на уроке пойдет об окружности. Заполняют кластер  4.Отвечают на поставленные вопросы, формулируют определения, сравнивают их с оригиналом, заполняют столбец

Индивидуальная работа и работа в парах

Познавательные  Поиск и выделение необходимой информации.

Регулятивные  выдвижение гипотез

Коммуникативные Умение слушать и вступать в диалог, работа в паре.

Личностные  умение выделять нравственный аспект поведения

IV.Изучение нового материала

Объяснение материала

Слайд 11

Слайд 12

Слайд 13

 Давайте  вспомним:

  1. сколько общих точек могут иметь две прямые, лежащие в одной плоскости?
  2. как называются данные прямые в каждом случае?

Изучите таблицу 4. Это ваша лабораторная работа. Подумайте, сколько возможно вариантов расположения прямой и окружности. Возьмите полоски самоклеящейся бумаги, которые будут являться прямой, и приклейте их так, как могла бы располагаться прямая и окружность на плоскости. Сколько вариантов  можно сделать?

Значит помимо того, что мы с вами вспомнили окружность, сегодня на уроке какую конкретно тему будем изучать? Запишите эту тему в своей лабораторной работе на индивидуальных картах.

1) одну, две, не имеют;

2) пересекающиеся, совпадающие, параллельные.

Изучают таблицу, приклеивают полоски бумаги так, чтобы получились 3 способа расположения прямой и окружности: 2 точки пересечения, 1 точка и не одной.

Формулируют тему: взаимное расположение прямой и окружности.

Фронтальная, индивидуальная работа

Познавательные  Поиск и выделение необходимой информации. Анализ объектов

Регулятивные: умение обрабатывать информацию

Коммуникативные умение достаточно полно и четко выражать свои мысли, слушать собеседника и вести диалог

Личностные: развивать мышление, воображение, внимание, наблюдательность

V.

Физ. пауза

Слайд 14 (динамическая пауза под музыку)

Сменить деятельность, обеспечить эмоциональную разгрузку учащихся.

Раз – поднялись потянулись,

Два – согнулись, разогнулись,

Три в ладоши три хлопка,

На четыре – три кивка,

Пять руками помахать,

Шесть – тихонько сесть

Учащиеся сменили вид деятельности (отдохнули) и готовы продолжать работу.

VI.Первичное осмысление и закрепление знаний

Осмысление способа перевода

Слайд 15

Слайд 16

Давайте вспомним,  когда расстояние от точки до прямой будет кротчайшим?

В своих лабораторных работах восстановите перпендикуляр от центра окружности до прямой в каждом из 3 случаев. Измерьте это расстояние и сравните его с радиусом окружности. Какие выводы можно сделать?

Кротчайшее расстояние-длина перпендикуляра. Измеряют расстояние и приходят к выводу, что радиус и расстояние до прямой связаны между собой и от их связи зависит кол-во точек пересечения.

Фронтальная индивидуальная

Познавательные Выделение и формулирование познавательной цели, рефлексия способов и условий действия. Анализ объектов и синтез

Регулятивные Планирование своей деятельности для решения поставленной задачи и контроль полученного результата

Коммуникативные Умение слушать и вступать в диалог, коллективное обсуждение проблем (при необходимости)

Личностные Ориентация в межличностных отношениях

VII.

Закрепление изученного на уроке, решение задач

Практическое применение понятия  

Слайд 17

Слайд 18,19,20

1. На слайде таблица, в которой представлена информация о радиусе окружности и расстоянии от центра окружности до прямой а. Используя числа 0, 1, 2 определите количество точек пересечения данной прямой и окружности.

1. R=16cм, d=12см

2. R=5см, d=4,2см

3. R=7,2дм, d=3,7дм

4. R=8 см, d=1,2дм

5. R=5 см, d=50мм

2.  Даны окружность с центром О и точка А. Где находится точка А, если радиус окружности равен   7 см, а длина отрезка ОА равна:

а) 4 см; б) 10 см; в) 70 мм. 

3. Попробуйте составить свою задачу на взаимное расположение прямой и окружности.

Комментирует,   направляет работу учащихся

Выступает в роли тьютора для слабых учащихся

Выдвигают свои версии, по желанию выходят к доске записывают результаты

Индивидуальная

Познавательные Выделение и формулирование познавательной цели, рефлексия способов и условий действия. Анализ и синтез объектов

Регулятивные Планирование своей деятельности для решения поставленной задачи,  контроль полученного результата, коррекция полученного результата, саморегуляция

Коммуникативные Умение слушать и вступать в диалог Поддержание здорового духа соперничества для

поддержания мотивации учебной деятельности

Личностные развитие самостоятельности учащихся на теории и практике

VIII.

Рефлксивно-оценочный этап

Зафиксировать  новые понятия  и алгоритм перевода величин

Слайд 21

Оцените свою деятельность на уроке.

Достигли ли вы поставленной цели на уроке?

Ответьте на вопросы со слайда

Выставление оценок.

Проводят самооценку   собственной учебной деятельности на листах самооценки. Показывают соответствующий смайлик.

Соотносят   цель урока и результаты ими полученные, фиксируют степень их соответствия.

Намечают дальнейшие цели деятельности

Фронтальная

Регулятивные:  Оценка промежуточных результатов и саморегуляция для повышения мотивации учебной деятельности

управление поведением партнёра- контроль, коррекция, оценка

Коммуникативные: умение полно и точно выражать свои мысли

Личностные: нравственно-этическая ориентация

IX.

Домашнее задание

Инструктаж учителя по выполнению домашнего задания 

Слайд 22,23

Использую знания полученные на уроке, заполните недостающие ячейки таблицы.

Спасибо за работу на уроке!

Учащиеся записывают домашнее задание

Познавательные: отработка алгоритма решения; творческая переработка изученной информации

Заместитель  директора по УВР________________________ / И.И. Салова/

ПРИЛОЖЕНИЕ 1

ИНДИВИДУАЛЬНАЯ КАРТА ЗНАНИЙ

Ф.И. _______________________________________________________________

ТАБЛИЦА 1.

Вопрос

«+»Верю, – Не верю

Проверка

1. Верите ли вы, что самая простая из кривых линий – окружность?

2. Верите ли вы, что древние индийцы считали самым важным элементом окружности радиус, хотя не знали такого слова?

3. Верите ли вы, что впервые термин “радиус” встречается лишь в 16 веке?

4. Верите ли вы, что в переводе с латинского радиус означает “луч”?

5. Верите ли вы, что в русском языке слово “круглый” означает высшую степень чего-либо?

6. Верите ли вы, что выражение “ходить по кругу” когда-то означало “прогресс”?

7. Верите ли вы, что определение “касательной” уже есть в первом учебнике геометрии — “Начала” Евклида?

8. Верите ли вы, что хорда в переводе с греческого означает “струна”?

ТАБЛИЦА 2

Что?

Кто?

Где?

Когда?

Почему?

Зачем?

КЛАСТЕР

ТАБЛИЦА 3

1

Окружность

Точки плоскости, одинаковое расстояние, точка — центр.

2

радиус

Точки окружности, центр окружности, отрезок.

3

Хорда

Отрезок, точки окружности.

4

Диаметр

Хорда окружности, центр окружности.

Сделайте вывод о взаимном расположении прямой и окружности, в зависимости от радиуса и расстояния от центра до прямой.

Радиус окружности меньше расстояния от центра окружности до прямой

Радиус окружности больше расстояния от центра окружности до прямой

Радиус окружности равен расстоянию от центра окружности до прямой

Прямая и окружность

____________________

Прямая и окружность

_____________

Прямая и окружность __________

Обсудите свои выводы с товарищем по парте.

ПРИЛОЖЕНИЕ 3

ЛАБОРАТОРНАЯ РАБОТА

Ф.И. ________________________________________________________________

ТЕМА РАБОТЫ: ______________________________________________________

Инструкция:

  1. Приклейте полоски так, как могут располагаться относительно друг друга на плоскости прямая и окружность.
  2. Сколько общих точек в каждом случае имеют эти прямая и окружность?
  3. Найдите расстояние от центра окружности до прямой и сравните его с радиусом окружности.

ОТВЕТЫ:

2)______________________________________________________________

3)______________________________________________________________

ПРИЛОЖЕНИЕ 2

“Ни 30 лет, ни 30 столетий не оказывают никакого влияния на ясность или на красоту геометрических истин”. Кэрролл Л.

Самая простая из кривых линий – окружность. Это одна из древнейших геометрических фигур. Ещё вавилоняне и древние индийцы считали самым важным элементом окружности – радиус. Слово это латинское и означает “луч”. В древности не было этого термина: Евклид и другие учёные говорили просто “прямая из центра”, Ф. Виет писал что “радиус” — это “элегантное слово”.

В Древней Греции круг и окружность считались венцом совершенства. Действительно в каждой своей точке окружность “устроена” одинаково, что позволяет ей как бы двигаться “по себе”. На плоскости этим свойством обладает еще лишь прямая.

В русском языке слово “круглый” тоже стало означать высокую степень чего-либо: “круглый отличник”, “круглый сирота” и даже “круглый дурак”.

Если вы когда-либо пробовали получить информацию от бюрократической организации, вас, скорее всего “погоняли по кругу”. Фраза “ходить по кругу” обычно не ассоциируется с прогрессом. Но в период индустриальной революции, выражение “ходить по кругу” очень точно отражало прогресс. Шкивы и механизмы давали машинам возможность увеличить производительность и значит сократить рабочую неделю.

Без понятия круга и окружности было бы трудно говорить о круговращении жизни. Круги повсюду вокруг нас. Представление об окружности даёт линия движения модели самолёта, прикреплённого шнуром к руке человека, также обод колеса, спицы которого соответствуют радиусам окружности.

Термин “хорда” (от греческого “струна”) был введён в современном смысле европейскими учёными в XII-XIII веках.

Определение касательной как прямой, имеющей с окружностью только одну общую точку, встречается впервые в учебнике “Элементы геометрии” французского математика Лежандра (1752-1833 гг.). В “Началах” Евклида даётся следующее определение: прямая касается круга, если она встречает круг, но при продолжении не пересекает его

(По материалам книг: Г. Глейзер “История математики в школе”, С Акимова “Занимательная математика”).

ПРИЛОЖЕНИЕ 4

ДОМАШНЕЕ ЗАДАНИЕ

Заполните таблицу.

Радиус окружности

4 см

6, 2 м

3,5 дм

1,8 см

Расстояние от центра окружности до прямой

7 см

5,12 м

3,5 дм

9,3 см

8,25 м

Вывод о взаимном расположении окружности и прямой

Прямая пересекает окружность

Прямая касается окружности

Прямая

не пересекает окружность

2) \ end {ases} $$

где

$$ \ begin {case} А = у_2 — у_1 \\ В = х_1 — х_2 \\ C = x_2 y_1 — x_1 y_2 \ end {ases} $$

Теперь вы можете использовать $ \ {x = \ frac {-b \ pm \ sqrt {\ Delta}} {2a}, y = — \ frac {Ax + C} {B} \} $ для определения точек. 2) \ end {ases} $$

Получить местоположение пересечения вектора / круга?

Давайте создадим уравнение, чтобы найти обе точки пересечения между линией и кругом, но сделаем это таким образом, чтобы было легко определить, какая из них (если она есть) находится между конечной точкой и начальной точкой вашего вектора.2 $$

с центром $ (h, k) $ и радиусом $ r $.

Ваш вектор будет иметь начальную точку $ (x_0, y_0) $ и конечную точку $ (x_1, y_1) $. Точки на линии, проходящей через эти две точки, будут заданы в параметрической форме следующим образом:

$$ x (t) = (x_1-x_0) t + x_0 $$ $$ y (t) = (y_1-y_0) t + y_0 $$

, где $ t $ — действительное число. В частности, эти точки строго между начальной и конечной точками соответствуют значениям $ 0 \ lt t \ lt 1 $.

Теперь, если мы заменим $ x, y $ в уравнении окружности параметризованными выражениями, мы получим квадратное уравнение относительно $ t $.2 — 4ac}} {2a} $$

Конечно, $ a $ будет положительным (если две точки, которые начинают и заканчивают вектор, различны), и $ c $ будет положительным, если начальная точка лежит вне круга. 2 — 4ac}} $$

, где правильный выбор знака был сделан таким образом, чтобы избежать ошибки «отмены».2 — 4ac $ необходимо проверить на положительный результат, а также окончательно проверить, что $ 0

Вставка корня $ t $ обратно в параметрическую форму прямой дает желаемую точку пересечения $ (x (t), y (t)) $.

Определить координату пересечения между линией и окружностью

Определить координату пересечения между линией и окружностью — Mathematics Stack Exchange
Сеть обмена стеком

Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.

Посетить Stack Exchange
  2. 0
  3. +0
  6. Авторизоваться Зарегистрироваться

Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях.Регистрация займет всего минуту.

Зарегистрируйтесь, чтобы присоединиться к этому сообществу

Кто угодно может задать вопрос

Кто угодно может ответить

Лучшие ответы голосуются и поднимаются наверх

Спросил

Просмотрено 11к раз

$ \ begingroup $

Я собираю в процессе обработки простой скрипт для визуализации возможностей компоновки в изменчивой среде веб-страницы.

Мне нужна помощь в вычислении точки на окружности:

Круг максимально велик, ограничен шириной или видимой высотой области просмотра веб-браузера, в зависимости от того, что меньше. Линия пересекает круг через его центр от одного угла окна просмотра / прямоугольника до противоположного угла.

Мой вопрос: как я могу вычислить координаты x и y пересечений линий на окружности круга?

[править] Забыл ссылку: http: // hascanvas.com / tschichold

Создан 27 апр.

Санхотефат

11311 золотых знаков11 серебряных знаков55 бронзовых знаков

$ \ endgroup $ $ \ begingroup $

Если линия и круг заданы в стандартной форме $ (x-a) ^ 2 + (y-b) ^ 2 = r ^ 2 $ и $ y = mx + c $, у вас есть два уравнения с двумя неизвестными.Просто вставьте выражение для $ y $ из линии в уравнение окружности, и вы получите квадратичный по $ x $, который даст (до) два решения. Если ваша линия и круг указаны по-разному, вероятно, будет работать аналогичный метод, но вам нужно определить, как они указаны.

Похожие записи

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *